外球面球轴承球径与球形测量方法分析与改进

杨泳烽

(浙江新昌皮尔轴承有限公司，浙江 新昌 312500)

外球面球轴承应是具有标准规定直径的球形外表面，且两端以球心为对称中心[1]。但由于加工方法及其制造工艺等因素的影响，实际制造的产品存在着一定的偏差，主要表现为球径偏差、球形偏差及位置偏差。而各轴承制造企业对于这些偏差所采用的测量与控制方法各不相同，并且各方法对于产品的影响也存在着较大的差异，因此实际加工出来的球面产品质量很不稳定，并最终影响到产品的装配质量及使用寿命。下文主要利用实践中常用的几种方法进行分析，并根据最终对产品测量结果的影响，提出改进办法。

1 外圈球面标准件的测量分析

1.1 外圈球面标准件最大直径及位置偏差的测量方法分析

在测量球径标准件时，一般都会选择测长仪，并利用标准量块与平行于基准端面的球面最大直径进行比较测量。测量时(图1)利用测长仪工作台调整被测标准件轴向与径向位置，从而找到产品的最大直径，但由于测头中心连线与实际球面最大直径可能会形成一定的夹角，从而产生标准件的测量误差。假设夹角α在±1° 范围内等概率分布，并以表1产品[2-4]作为测量标准件，对由此引起的测量误差进行分析。

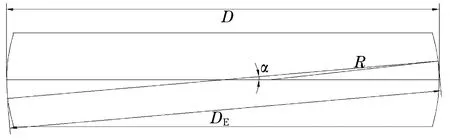
图1 球面标准件最大直径测量示意图

表1 假设标准件测量型号列表 mm

表1中ΔDh为负号时，代表以较大一面作为测量基准面。根据表1及图1可推导出夹角α与测量误差值ΔDα的关系。

ΔDα=DE-D，

ΔDα=(D-2R)cosα-D-[(D2-4DR)·

(1)

式中：DE为测长仪测量尺寸。由(1)式可分别求得3种型号标准件的测量误差值，见表2。

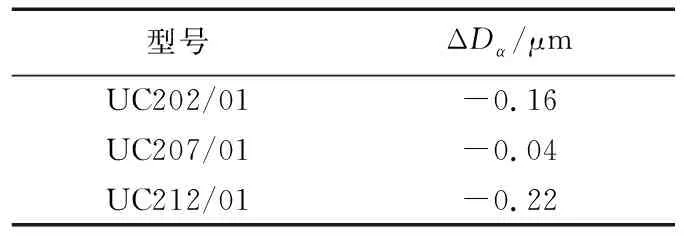
表2 标准件的球面最大直径测量误差

由此可以看出，夹角α对于标淮件最大直径测量误差的影响很小，但在实际应用时，由于采用轴仪测量的方式，测量高度固定，标准件作为比较测量时的一个参考标准，因此，当球面标准件的最大直径偏离对称度中心一定距离时，就会影响到产品的测量结果，故需要对这一偏离距离进行计算。而通过测量两端面等高的球弦直径差ΔDh，并利用这一差值推导出标准件对称度t，即计算出最大直径偏离球面对称中心的距离A1。若同样以表1为相同条件，由图2知

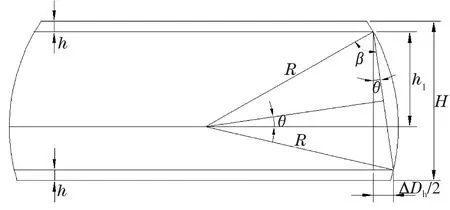
图2 两端球弦差对对称度偏差影响分析图

H/2-h+T/2=h1,

h1=Rsin [arcsin (90°-β)+arctanθ]，

(2)

式中：T为测量面弦高与对称测量面相同高度位置的弦高差，对称度t=|T|。从(2)式可以得到不同型号标准件偏离球面对称中心高度，见表3。

表3 标准件偏离球面对称中心的距离 mm

在实际计算对称度t时，由于球面曲率的差异对于对称度的影响很小，可用R=D/2进行计算。

1.2 标准件球弦直径偏差的测量方法分析

实际生产中，为了能同时控制球形及位置偏差，在测量两端球弦差的同时，也会对球弦直径进行控制，这就需要得到标准件支点高度h位置的球弦直径偏差值。但由于受测长仪高度调整误差的影响，通常采用测量球面对角尺寸的方式，即在测量时，通过调整垫块或工作台角度使被测标准件的最大直径刚好通过支点高度h的位置,但由于该高度位置采用划线目视的办法，因此有可能产生一个β角的偏离，根据经验β角可控制在±1°偏差范围内，若以表1相同条件测量支点高度h=1.5 mm处的球弦直径标准件，则可根据条件先计算出该对角尺寸测量时的理论调整倾角θ(图3)。

图3 球面对角尺寸测量角度调整分析图

(3)

根据求得的θ角，可参照 (1) 式计算出相应的对角尺寸Dθ，并根据相应支点高度，利用 (4) 式计算出球弦标准件实际偏差值Δh(图4)，以及由β角偏差所引起的球弦标准件的测量误差ΔDθ。

图4 标准球弦直径偏差值计算分析图

(4)

式中：DSφ为标准球径；Dθ为实际对角尺寸。计算结果见表4。

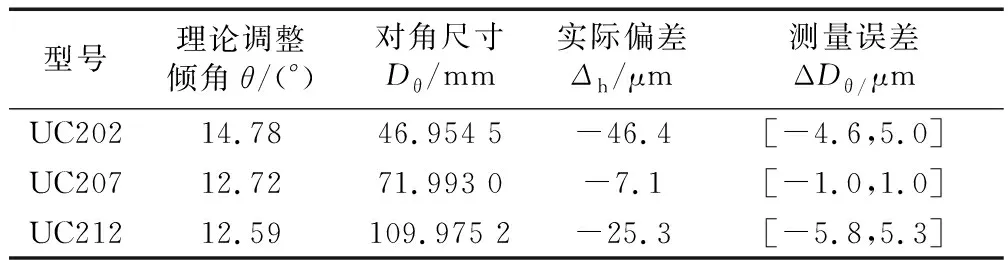
表4 球弦标准件的测量误差与实际偏差

从而可以看出，当球形偏差越大时，产生的球弦标准测量误差也越大，因此，在选择标准件时，应尽量选择球形偏差较小的产品。

2 生产过程中球径与球形测量控制方法分析

2.1 球面最大直径测量

在生产过程中，有不少企业选择用D913轴仪进行球面最大直径的测量，其结构如图5所示。

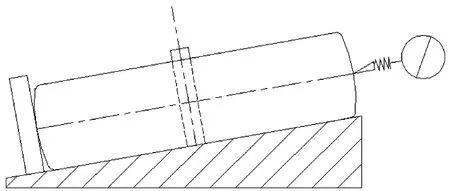
图5 D913轴仪最大直径测量结构示意图

图5所示为测量平行于基准端面的球面最大直径，采用圆柱体支承，并通过调整表针高度位置，从而找到球面标准件的最大直径。此测量方法的误差影响因素主要包括：

(1)标准件与测量产品的宽度差引起的最大直径测量高度的差异。

(2)标准件与测量产品的对称度偏差引起的最大直径测量高度的差异。

(3)标准件与测量产品的球形差引起的直径测量误差。

(4)标准件与测量产品直径差引起的最大直径测量位置的偏离。

(5)支承与轴仪工作台之间垂直度及表针接触位置变动的影响。

(6)轴仪测量精度及标准件的测量误差。

针对以上6个影响因素，以表1中产品作为标准件进行误差分析。

①根据表1中3种型号标准件的实际宽度，以及标准宽度范围内所可能出现的最大宽度差值，分别求得标准件与测量产品宽度差而引起的最大直径测量高度差A2。

②根据产品加工时两端球弦差的控制要求(|ΔDh|≤0.01 mm)，以及标准宽度范围，分别假设测量产品见表5，并可利用(2)式，分别求得假设测量产品对称度偏差而引起的最大直径测量高度差A3。

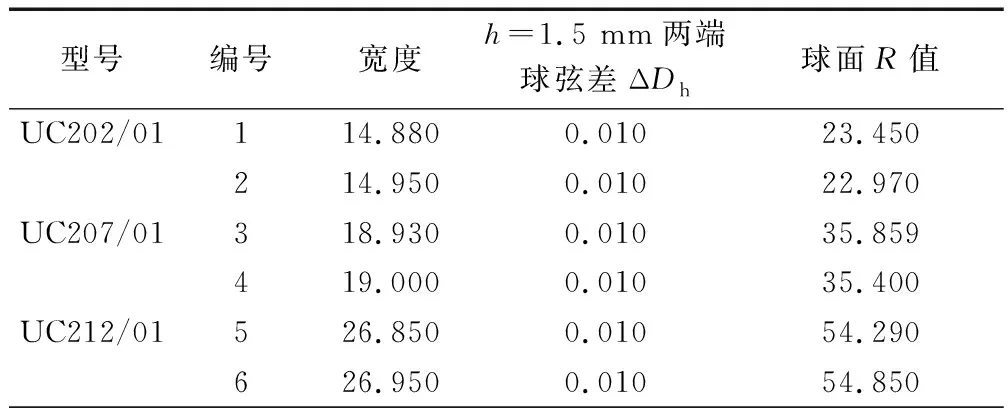
表5 假设测量产品列表 mm

③由于D913轴仪表针测量高度固定，若产品与标准件最大直径的测量高度存在着一定的差异，由此会产生一定的直径测量误差，根据表3得到的A1及可能引起的高度差A2，A3，可计算出产品与标准件直径测量位置的最大高度差为A=A1+A2+A3，则

(5)

计算结果见表6，可以看出，(1)～(3)项因素对于直径测量误差的影响很小，而(4)，(5)项因素是在前3项因素的基础上可能产生的误差分量，因此，其影响值可以忽略不计。根据D913轴仪的示值允许误差±1 μm以及表2的球面最大直径测量误差，可知用该方法测量球面最大直径，其误差可控制在1.5 μm以内，完全可以满足产品最大直径测量控制的要求。

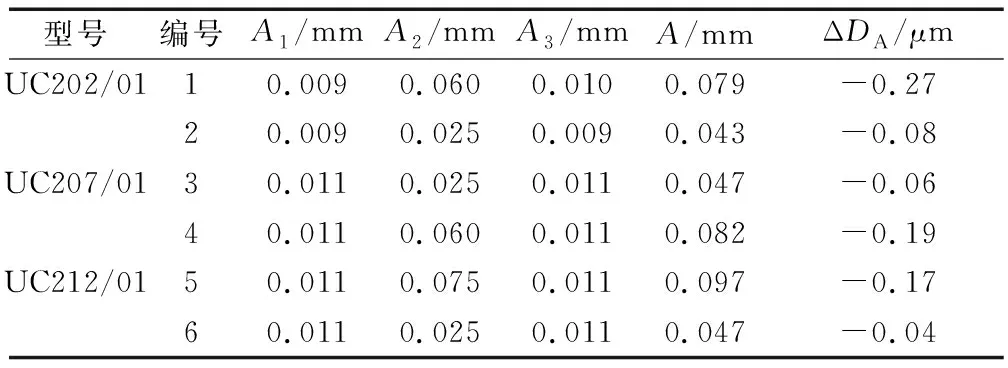
表6 对应编号产品的直径测量误差

2.2 球形偏差测量控制

目前，企业在生产过程中，都是采用间接测量的方式控制球形偏差，虽然也有企业采用托盘摆动测量方法直接测量球径与球形偏差，但该方法测量时必须要保证托盘摆动的支点中心与被测产品球心处于同一水平高度，当两者存在一定高度差异而带动产品摆动时，就会造成产品的位置偏移；而且由于支承位置的固定，产品在摆动时会产生滑移，并偏离球心和测量截面中心，从而造成一定的测量误差，并且这种误差会随着托盘摆动角的增大而增大，因此，不少企业还是选择以测量球弦直径的办法控制球形偏差，并且较多选择D913轴仪进行测量，其测量结构如图6所示。

图6 D913轴仪球弦直径测量结构示意图

在实际测量球弦直径时，同样存在着一定的测量误差影响因素，从而影响球形偏差的控制，主要包括：

(1) 轴仪支承高度调整误差引起标准件的球弦直径测量误差。

(2) 标准件与测量产品的宽度差引起产品球弦直径的测量误差。

(3) 产品对称度偏差引起的产品球弦直径测量误差。

(4) 球弦直径标准件的测量误差。

(5) 轴仪测量精度引起的球弦直径测量误差。

针对以上5点影响因素，并以表1中产品为标准件，通过测量球弦直径的方式，对球形偏差控制范围的影响进行分析。

①轴仪支承调整时，可采用卡尺和红油划线等办法减少其高度调整误差，但最终受目测影响，调整时误差可控制在±0.3 mm范围内。当假设支承高度h=1.5 mm，则实际支承高度应在1.2～1.8 mm内等概率分布；而受到标准件对称度的影响，标准件的实际测量弦高应在Zh±0.3 mm范围内等概率分布，即Zh=(H/2-h+T/2)。根据表1标准件的球面最大直径D与R值以及表4球弦标准件实际偏差Δh，可以计算出相应的对应弦高尺寸Lh及球弦标准控制尺寸Dh，见表7。

表7 对应球弦标准的实际控制尺寸

(6)

②根据求得的球弦标准控制尺寸Dh，并参照表5测量产品相同条件，利用 (2) 式求出对应编号产品对称度t，并以表7标准实际测量弦高相同方法计算出产品实际测量弦高Zh，从而根据实际对应支点高度的球弦标准控制尺寸及产品实际测量弦高，利用 (7) 式求出产品测量时所能控制的球面对角尺寸Dθ，见表8。

表8 对应编号产品的球面对角尺寸范围 mm

(7)

表中的球面对角尺寸Dθ是在不考虑球弦标准测量误差以及球弦标准控制偏差的情况下计算得到的，而当球弦标准件测量误差ΔDθ=±1 μm，再由球弦标准控制偏差(即表1标准球径偏差)求得球弦标准控制尺寸范围，并同样根据 (7) 式求出对角尺寸Dθ范围，并由已知D913轴仪的示值允许误差±1 μm，最终可计算出产品所可能出现的最大球形偏差，见表9。

表9 对应编号产品最大球形偏差 μm

由表9可以看出，即使在较好控制产品宽度偏差的前提下，此测量方法引起的最大球形偏差仍远大于标准所规定的偏差值范围，因此，其球形质量控制的稳定性很难得到保证。

2.3 球形偏差测量控制方法的改进

2.3.1 对角球弦直径升降测量法

该装置(图7)与D913轴仪的测量结构基本类似，由2个定位支承和1个量表组成。其中测量定位支承与量表的高度可根据两端面支点高度位置分别进行调整，而产品定位支承则可根据产品最大直径的测量位置进行调整固定，测量时可通过微调装置调整工作台高度，从而找到量表的最大值。由于最大值在表针与定位支承相对于球心对称中心的位置，即对角球弦直径测量位置，因此每一产品的测量弦高都是相等的，刚好可以消除产品宽度差及对称度对测量结果的影响，因此影响该装置测量结果的主要因素就只有标准件测量误差、支承高度调整误差以及该装置自身的示值误差。若以表1和表5相同设定条件进行测量分析，并假设该装置量表表针与定位支承之间的高度调整误差在 ±0.6 mm范围内等概率分布，则根据表1标准件宽度及测量支点高度，分别计算出量表表针与定位支承之间的高度C=(H-2h±0.06)mm，并以下式求得标准件相应高度的对角球弦直径LC,

1—立柱；2—产品定位支承；3—产品；4—量表；5—螺母；6—螺钉；7—螺栓；8—测量定位支承；9—可调升降工作台；10—导槽；11—微调装置图7 对角球弦直径升降测量装置

(8)

根据表4求得的球弦标准偏差及假定球弦标准件测量误差ΔDθ=±1 μm，可求得对角球弦控制的标准尺寸DC，而由于该测量装置不受产品宽度差及对称度影响，对每一个测量产品的球面对角尺寸都满足

(9)

因此，可根据对角球弦直径的偏差控制范围(即表1标准球径偏差)，求出这3种型号产品球面对角尺寸Dθ的控制范围，见表10。

表10 对角球弦直径升降测量所控制的球面对角尺寸范围 mm

在实际制作和安装过程中，该装置定位支承和量表表头中心连线与测量轴线会形成一定的夹角，即产生错位现象，由此会形成一定的理论测量误差，但由于采用比较测量的方式，当标准件与测量产品的对角球弦直径越接近时，错位引起的测量误差越小，当两者差值控制在0.05 mm以内，该误差≤1 μm[5]，因此，根据表10及该装置产品测量时的误差量，可以判定该装置完全能够满足产品球形偏差的控制要求。

2.3.2 球面刮色或目测判定法

在生产现场，很多企业在采用轴仪测量的同时，也会利用卡板进行控制，而现有的球面卡板一般都采用刀片式结构，利用卡板与球面之间的间隙量判定R值的大小，而实际操作时，卡板相对于球面的角度和位置极易产生偏离，这就会产生误判现象。因此，为了提高目测方法的准确性，根据原有控制方法，并利用球形的任一截面都为标准圆这一原理，设计出如图8所示的判定装置。

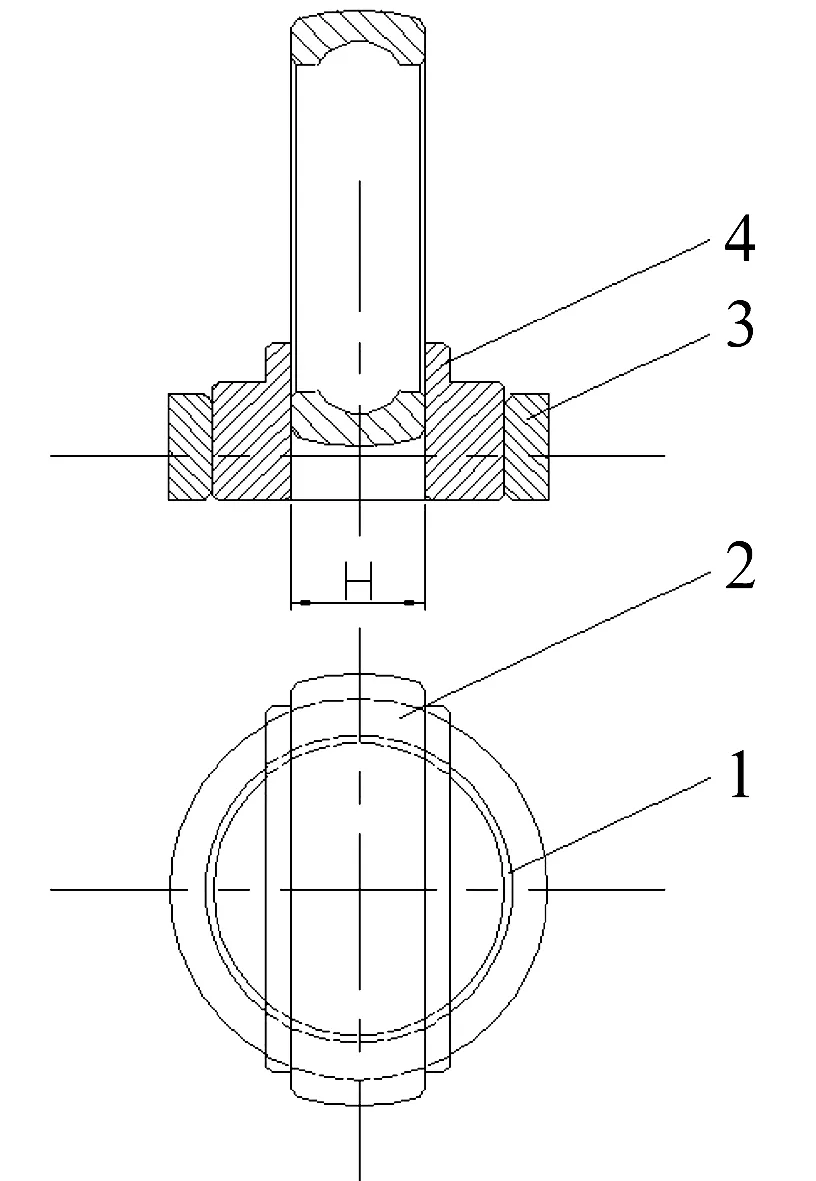
1—刮圈圆角；2—产品；3—刮圈；4—挡板图8 球面刮色和目测装置

该球面目测判定装置由经过圆角处理的刮圈与2个挡板组成，其中2个挡板可固定且相互距离H为球面产品的最大宽度值，操作时，可将球面产品放置在2个挡板中间进行观测，同时也可利用红油对球面进行着色，并将该产品放置在2个挡板中间，稍用力下压并进行旋转，通过观察剩余着色量来判断其球形偏差，而在实际应用时，则需要特别注意以下因素对判定结果的影响：(1)刮圈圆角任一轴向截面圆度误差而引起的剩余着色量误差；(2)剩余着色量多少的差异而引起的判定误差。

为了减少因素(1)对判定结果的影响，可通过改进工艺的办法进行保证，而针对影响因素(2)可以通过试验(表11)得到证明。

表11 球形误差相对应剩余着色量的对比分析

由表11可以看出，球面最大直径与对角尺寸的差值大小直接影响到剩余着色比例及目测状态，而这一差值正好反映了球形误差量，因而，采用这一方法也可以判定球形超差产品，达到控制产品质量的目的。

3 结束语

(1)在测量标准件时，球形偏差的大小会影响球弦标准件的测量误差，也会影响产品的最终测量结果，因此，在选择标准件时应选择球形偏差较小的产品作为标准件。

(2)以D913轴仪测量球面最大直径，可将误差控制在1.5 μm以内，完全可以满足产品球径偏差的控制要求。

(3)以D913轴仪测量两端球弦差来控制产品的对称度，同样可以满足产品位置偏差的控制要求。

(4)通过D913轴仪测量球弦直径的方式间接控制球形偏差，由于球弦直径的测量偏差范围过大，因此其球形偏差很难得到控制，若采用对角球弦直径升降测量法，则完全可以满足产品球形偏差的控制要求；而采用球面刮色或间隙判定法，则可以准确地判定出球形超差产品。