基于SG滤波器和组合窗STFT的滚动轴承故障诊断方法

王勇，邓四二，王恒迪

(河南科技大学 机电工程学院，河南 洛阳 471003)

滚动轴承的振动信号往往表现为非平稳特征，当有局部损伤存在时，如何从非平稳的振动信号中提取出故障信息是滚动轴承故障诊断的关键问题。短时Fourier变换(short-time Fourier transform,STFT)是一种联合时频分析方法[1]，表征了非平稳信号频率随时间的变化关系，能够得到信号在时域和频域内的全貌和局部信息，是一种实用的非平稳信号故障诊断方法。然而由于传统的STFT变换采用固定的窗函数[2]，无法同时满足高的时间分辨率和频率分辨率；而且目前自适应窗函数[3]的计算量较大，可靠性也有待进一步验证。另外，振动信号中往往存在着较强的窄带脉冲和随机噪声干扰，会严重影响STFT的分析精度，因此在STFT变换之前需要采用合适的方法对振动信号进行预处理。基于以上原因，提出了一种基于SG(Savitzky-Golay)滤波和组合窗STFT的滚动轴承故障诊断方法。该方法将SG滤波器[4-5]作为STFT的前置滤波单元，对信号滤波消噪后再利用长、短2个窗函数设计出一个新的组合窗[6]，利用组合窗提高STFT的时频分辨率并应用于轴承振动信号分析。

1 基于SG滤波器的组合窗STFT

1.1 SG滤波器

SG滤波器是根据多项式最小平方拟合方法导出的滤波器，与传统滤波器相比，其优点是形式简单、计算量小、无需确定滤波器的截止频率，能够显著地提高信噪比。其推导过程如下：

设一组数据为xi,i=-M，…，0，…，M，现构造一个p阶多项式yi来拟合xi，

p≤2M。

(1)

总的拟合误差为

(2)

为了使拟合误差e最小，令e对ar的偏导数为零，即

r=0，1，…，p，

(3)

整理(3)式可得

(4)

实际应用时(4)式取M=2，p=3即可满足平滑滤波的要求，解出a0，a1，a2，a3代入(1)式，并令i=0，±1，±2,得到y-2，y-1，y0，y1，y2共5个点的表达式。由于yi最高阶次为3，故此时的SG滤波器又可以称为五点三次平滑法。当xi的点数较多时，xi的起始点分别用y-2和y-1表示，中间点均用y0表示，末尾2点分别用y1和y2表示。

;i=3,4,…,n-2。

(5)

需要注意的是，五点三次平滑法会使波形的峰值降低，造成拟合误差增大，因此平滑次数不宜过多。

1.2 组合窗STFT

STFT是一种非线性信号分析方法，能够同时提供时域和频域的局部信息，在旋转机械的振动分析中发挥了很大作用。STFT的基本思想是把信号划分成许多小的时间间隔，然后用一个窗函数g(t-τ)对信号x(t)的乘积运算实现在τ附近的平移，再用Fourier变换分析每一个时间间隔，以确定时间间隔内存在的频率成分。

信号x(t)的STFT定义为

(6)

式中：g(t-τ)是中心为τ的窗函数，起时限作用；e-j2πft起频限作用。分别令x(t)=δ(t-τ0)，x(t)=exp(jw0t)，得

STFTX(w,τ)=exp(-jwt0)g(t-t0)，

(7)

STFTX(w,τ)=exp[-j(w-w0)]g′(w-w0)。

(8)

(7)式和(8)式表明信号的STFT分析结果受窗函数的影响很大，高的时间分辨率需要较短的窗函数，而高的频率分辨率需要较长的窗函数。由Heisenberg不确定原理可知，高的时间分辨率和频率分辨率无法同时满足。在进行STFT分析时，时频窗不具有自适应性，无法自动改变其大小，窗函数一旦确定，则在整个分析过程中在时间-频率平面上的所有局域分辨精度都是相同的，因此传统STFT方法在分析轴承振动信号时，很难准确地提取出故障信息。

1.3 改进STFT

针对传统STFT方法的不足，采用长、短窗函数相结合的方式对STFT进行改进，其原理如下：若信号能量分布在时间区间[-t,t]和频率区间[-f,f]，则在区间[-t,t]×[-f,f]上进行STFT变换，信号能量基本不会泄漏。因此首先用SG滤波器得到降噪信号，然后选择一个长窗函数和一个短窗函数分别对原始振动信号进行STFT变换，再把两者相乘就实现了改进的STFT变换，具体实现过程如图1所示。

图1 基于SG滤波器的组合窗STFT的实现过程

2 仿真分析

仿真信号x(t)的时域波形如图2a所示，其由3个受到白噪声干扰的正弦信号组成，正弦信号的频率分别为100，200和300 Hz，幅值依次降低。图2b是采用1/2数据长度的Hanning窗对x(t)直接进行STFT变换求得的时频图谱，从图中可以看出，由于受到了白噪声的干扰，正弦信号的3个频率成分很难被识别出来。图2c是用SG滤波器对图2b所示的时频图谱进行降噪处理后的结果。从图中可以看出，白噪声的影响大大降低，3个频率成分已经被识别出来，然而谱线较为模糊，300 Hz的频率成分几乎看不到。图2d是用图1所示方法，先用SG滤波器对振动信号降噪，然后用1/2数据长度的Hanning窗和1/8数据长度的Hanning窗得到组合窗对x(t)进行STFT变换求得的时频图谱，从图中可以清晰地看到100，200，300 Hz的频率成分，与图2c相比，大大提高了时频分辨率。

图2 仿真信号的时频分析方法对比

仿真分析的结果表明，与传统的固定窗STFT变换相比，基于SG滤波器的组合窗STFT不仅可以抑制随机噪声的干扰，而且能够获得更高的时频分辨率，提高了STFT变换的精度。

3 试验验证

试验轴承型号为6203和6012，其中6203的内径为17 mm，外径为40 mm，钢球直径为6.747 mm，钢球个数为8；6012的内径为60 mm，外径为110 mm，钢球直径为15.08 mm，钢球个数为10。根据6203和6012的基本参数求得的理论故障频率见表1。

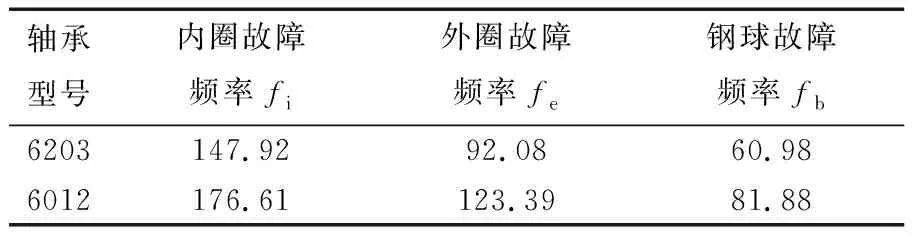
表1 6203和6012的理论故障频率 Hz

轴承振动信号的采样频率为40 000 Hz，采样点数为5 000。下面是测振仪上得到的2种典型振动信号的分析结果。

图3a是6203外圈损伤振动速度信号，图3b是采用长度为1/4的Hanning窗进行STFT变换求得的时频谱，图3c是用组合窗法得到的时频分布图(组合窗是一个1/4数据长度的Hanning窗和长度为1/16的Hanning窗)。对比图3b和图3c可见，改进的STFT谱线更加清晰，明显提高了时频分辨率，比传统方法更为准确。从图3c可以清晰地看到2条谱线的时间间隔ΔT约为0.011 s，即轴承的故障频率为1/ΔT=90.9 Hz，与6203的理论故障频率对比可知该故障频率与外圈故障频率(92.08 Hz)较接近，因此可以判断该轴承的故障部位在外圈上。

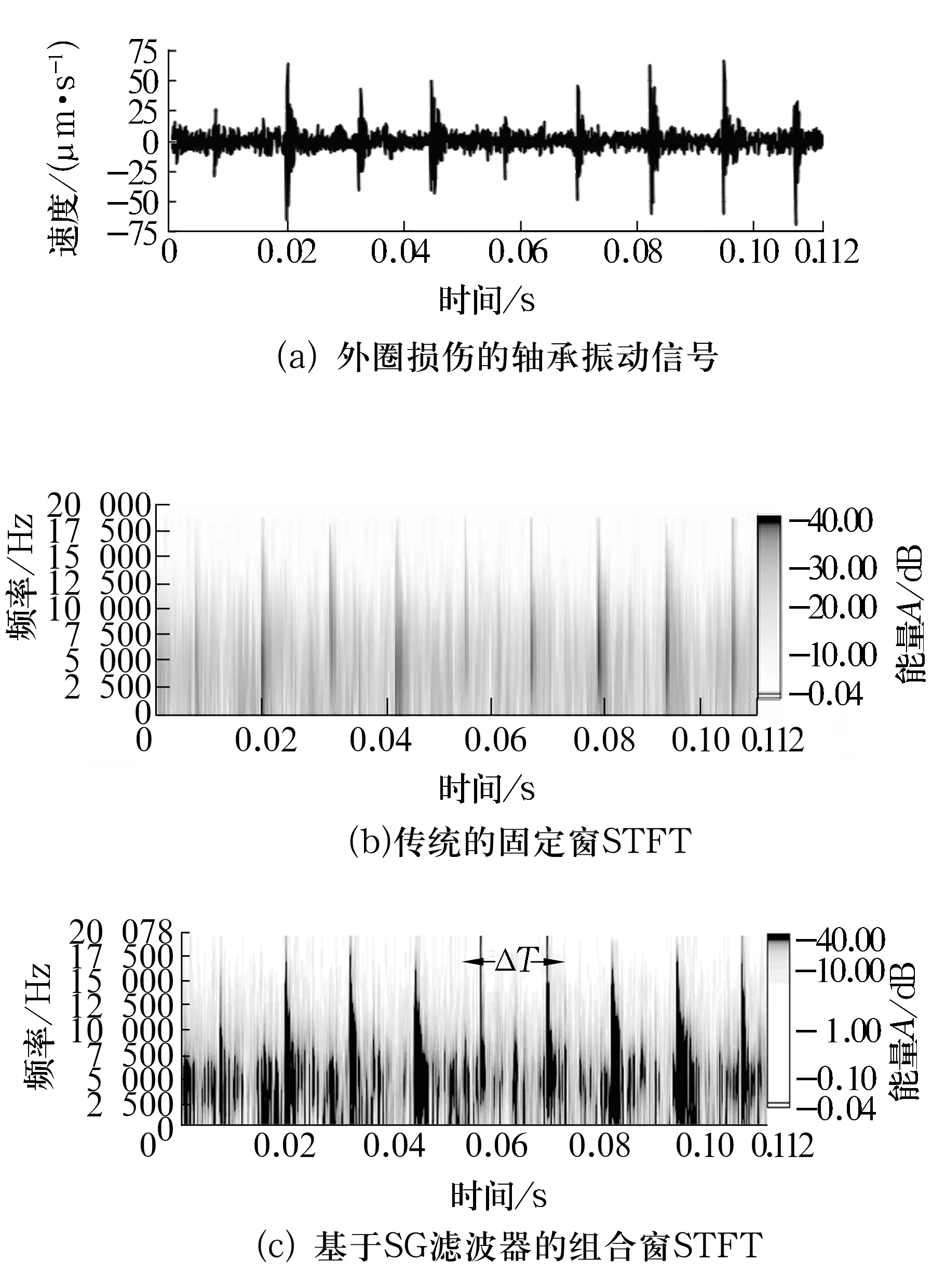
图3 6203外圈损伤的时频分析方法对比

图4a是6012外圈有轻微损伤的振动速度信号，图4b是采用1/4数据长度的Hanning窗进行STFT变换求得的时频谱，图4c是用基于SG滤波器的组合窗STFT求得的时频分布图，其中组合窗是一个1/4数据长度的Hanning窗和一个1/16数据长度的Hanning窗。对比图4b和图4c可知，传统的固定窗函数STFT诊断效果较差，而组合窗STFT明显提高了时频分辨率，更易发现轴承故障。从图4c可以清晰地看到2条谱线的时间间隔ΔT约为0.008 s，即轴承的故障频率为1/ΔT=125 Hz，和6012的理论故障频率对比可知该故障频率与外圈故障频率(123.39 Hz)较接近，因此可以判断该轴承的故障部位发生在外圈上。

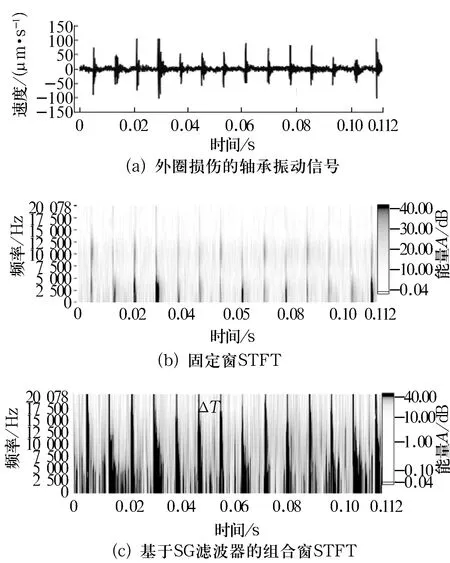
图4 6012外圈损伤的时频分析方法对比

4 结束语

提出了一种基于SG滤波的组合窗STFT的滚动轴承故障诊断方法，将SG滤波器用于振动信号去噪，采用长、短窗函数获得2组STFT时频表示并以乘积结果作为最终时频表示的组合窗。数值仿真和轴承故障诊断实例的结果表明，该方法能更加有效地增大信噪比，与传统的固定窗函数相比，组合窗STFT变换的时频聚集性得到了很大提高，突出了故障振动信号的故障特征，提高了故障诊断的准确性。