基于形态成分分析的轴承复合故障诊断

2011-07-23杨杰郑海起关贞珍王彦刚

轴承 2011年8期

杨杰，郑海起，关贞珍，王彦刚

(石家庄军械工程学院，石家庄 050003)

当齿轮箱出现故障时，有时可能不只存在一种故障，可能是多种故障状态并存，盲源分离为齿轮箱多故障并存的分离提供了新的方法，在齿轮箱故障诊断中已经得到成功的应用[1-2]。

在盲源分离算法中，经典的独立分量分析(ICA)方法假设源信号是独立统计的。虽然目前ICA方法在许多应用中已证明是成功的[3-4]，但其基于统计独立的假设条件并不适用于所有情况。特别是在实际应用中，很多信号或图像具有稀疏性，或者经适当的变换，使其在变换域中具有较好的稀疏性。当源信号是高度稀疏时，这表示每个源信号只有很少的时刻取值为非零(或者较大)，而绝大多数时刻取值为零(或者接近零)。在这种情况下的独立假设意味着2个源信号同时为有用信号的概率极低，因此源信号可以由不同的基函数表示。在稀疏成分分析(Sparse Component Analysis, SCA)中就利用了这一点[5-6]。

最近，又提出了另外一种基于信号稀疏表示的分离方法——形态成分分析(Morphological Component Analysis，MCA)[7-8]。该方法假设对于混合信号中的每个源信号，都存在着相对应的能够稀疏表示该源信号的字典，并且认为该字典仅能稀疏表示该源信号，对于其他源信号则不能稀疏表示；然后利用追踪算法搜索最稀疏的表示，从而产生理想的分离效果。下文尝试把该方法引入到轴承复合故障分离中，为齿轮箱故障诊断探索新的理论方法。

1 信号的稀疏分解

正交线性变换在信号处理中具有非常重要的地位和作用，如Fourier变换和小波变换等，在这些方法中，通过基函数展开将信号表示为一系列基函数线性加权和的形式进行分析，然而，工程实践中对于任意复杂多变信号，传统的基函数展开方法在信号表示方面缺乏自适应性。为了对任意复杂多变的信号进行表示，人们试图寻找建立在多种基函数基础之上的信号表示方法，稀疏分解即是为了实现这一目标而提出的新的信号处理方法，其基本思想是基函数用称之为字典的超完备的冗余函数系统取代，字典中的元素被称为原子，信号由原子的线性组合来表示。其中原子的数目比信号的维数大，由此产生了冗余。由于这种超完备性，就有很多表示信号的方法，其中具有最少系数(最稀疏)的表示是最简单的，也是认为最优的一种表示方法。

对于任意信号s∈RN，要想找到最稀疏的表示，等同于解决下列问题

(1)

式中：‖u‖0为系数矢量u中非零项的个数，在一个随机的冗余字典T中寻找信号的稀疏表示，这是非凸和高度非光滑的，是一个NP难问题。

为了解决这个问题，文献[9]引入了匹配追踪(marching pursuit，MP)算法。近几年，匹配追踪算法得到了很大的发展，显示出很大的优越性。然而匹配追踪算法由于在算法过程中需要进行大量的内积运算和字典的选择，计算量巨大，限制了它在很多领域的运用。同时，匹配追踪算法信号表示的精度问题也限制了其应用。

为了解决信号稀疏表示和分解问题，又提出了基追踪(basis pursuit，BP)算法，把(P0)问题转化为(P1)问题

(2)

即把最小化l0范数转化为最小化l1范数，使问题简单化。对于最小化l1范数，可以通过线性规划方法解决。基追踪去噪(Basis Pursuit Denoising， BPDN)[10]是BP算法的推广，把(P1)问题变成无约束优化问题

(3)

其中参数λ控制着表示信号s时的失真度。(P1,λ)具有二次规划结构，可以通过很多方法进行求解。当T选择为酉矩阵时存在封闭解

(4)

其中，ηλ(x)=sign(x)(|x|-λ)+，

2 形态成分分析

(5)

(6)

Stark在BCR(Block-Coordinate-Relaxation)方法[11]的基础上，给出了MCA的数值实现：

(1)初始化迭代次数Lmax及阈值δk=λk·Lmax/2；

(2)Whileδk>λk/2

fork=1,…,n；

假设sk′≠k不变，更新sk：

计算剩余量rk=s-∑k′≠ksk′；

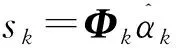
更新阈值δk=δk-λk/2。

MCA算法只能分离同一信号中具有不同形态的信号分量。文献[12]将MCA扩展到多通道数据情况下，提出了GMCA(Generalized MCA)算法，GMCA是一种快速有效的盲源分离方法，充分利用了形态多样性和稀疏性的特点，把源看作是形态成分的线性组合，并利用稀疏性估计源和混合矩阵，取得了较好的试验结果。文献[13]将该方法应用到了脑信号分离中。

对于线性混叠模型

X=AS+N，

(7)

设源信号是统计独立的，且每个源信号sk是不同形态成分的线性组合，

(8)

Tk和Rk分别表示与冗余字典Φk相关的正逆变换，(8)式中，φk,i为sk的1个形态成分，可以由变换Tk稀疏化，且仅能由Tk稀疏化。则估计模型(7)中的混叠矩阵A和源信号S转化为求解以下优化问题

(9)

(1)初始化递归次数Lmax和阈值：∀k,δk=

Lmax·λk/2;

(2)Whileδk>λk/2

fork=1,…,n;

(3)假设sk′≠k和ak′不变，更新sk：

(4)设源信号不变，更新A；

(5)对∀k，重正规化ak,sk和δk；

(6)对∀k，减小阈值δk=δk-λk/2。

在步骤(4)中，在由MCA算法得到的源信号的稀疏分解系数α={αk,i}的基础上，混叠矩阵A的估计基于如下的更新策略

(10)

式中：β为归一化常量；I为属于Rm的单位矩阵；γ为与源信号参数的假设概率分布有关的非线性函数向量。

3 仿真信号分析

为了检验GMCA盲分离算法的有效性，进行了如下的仿真，取m=2，n=2，即2个传感器、2个源信号的盲分离。

设2个源信号分别为

sin(2π×0.01t)+n(t),

sin(2π×0.035t)+n(t),

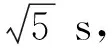
随机选取混合矩阵为

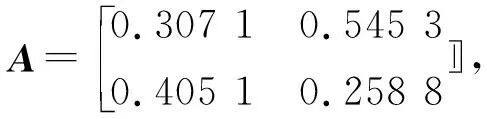
将2路信号线性混合并叠加3 dB的高斯白噪声，得到混叠信号如图1所示。

图1 混叠信号时域图

构造Fourier字典和基于8阶消失矩Symlet小波字典，由GMCA算法得到混合矩阵A的估计

由GMCA算法分离得到的源信号如图2所示，可以看出，源信号被较好地分离出来，且噪声较小。FICA分离的源信号如图3所示，很明显，分离信号与原始信号差别很大。

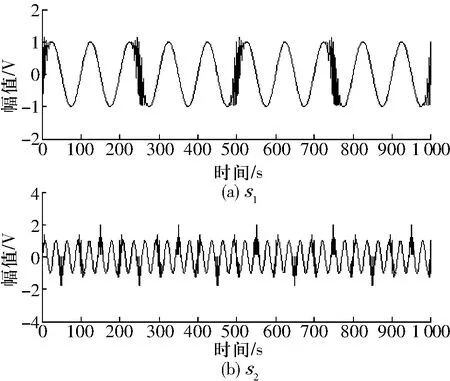
图2 GMCA分离信号时域图

图3 FICA分离信号时域图

为进一步反映源信号的分离效果，引入信噪比和误差指标进行评价，结果见表1。由表中可以看出，GMCA对带噪信号的分离效果明显好于FICA，同时也说明了GMCA分离算法的有效性。

表1 分离方法效果对比

4 齿轮箱复合故障信号分析

在某型单级齿轮箱上进行试验验证。该系统由电动机带动输入轴，输出轴带动负载。主动齿轮齿数Z1=30，被动齿轮齿数Z2=50，输入轴轴承型号为6206，输出轴轴承型号为7207，故障是在输入轴轴承内圈、外圈和滚动体通过线切割实现的，对振动信号在时域里进行等时间间隔采样，采样频率为12 800 Hz，测量时转速为1 200 r/min，采样时间长度为0.25 s。6206轴承内径为9.5 mm，外径为46.5 mm，接触角为0°，滚动体数目为9，根据轴承的结构尺寸和工作转速，可以计算出内圈故障特征频率108.4 Hz，滚动体故障特征频率94.2 Hz，外圈故障特征频率为71.6 Hz。

在输入轴两端轴承座的上部各安装1个传感器，并在输入轴一端轴承座的下部安装1个传感器，传感器的型号为B&K4508加速度传感器，3个传感器采集的振动信号频谱如图4所示，可以看出采集信号的几个故障特征频率在每一个频谱图上混叠，难以确定哪些故障存在。

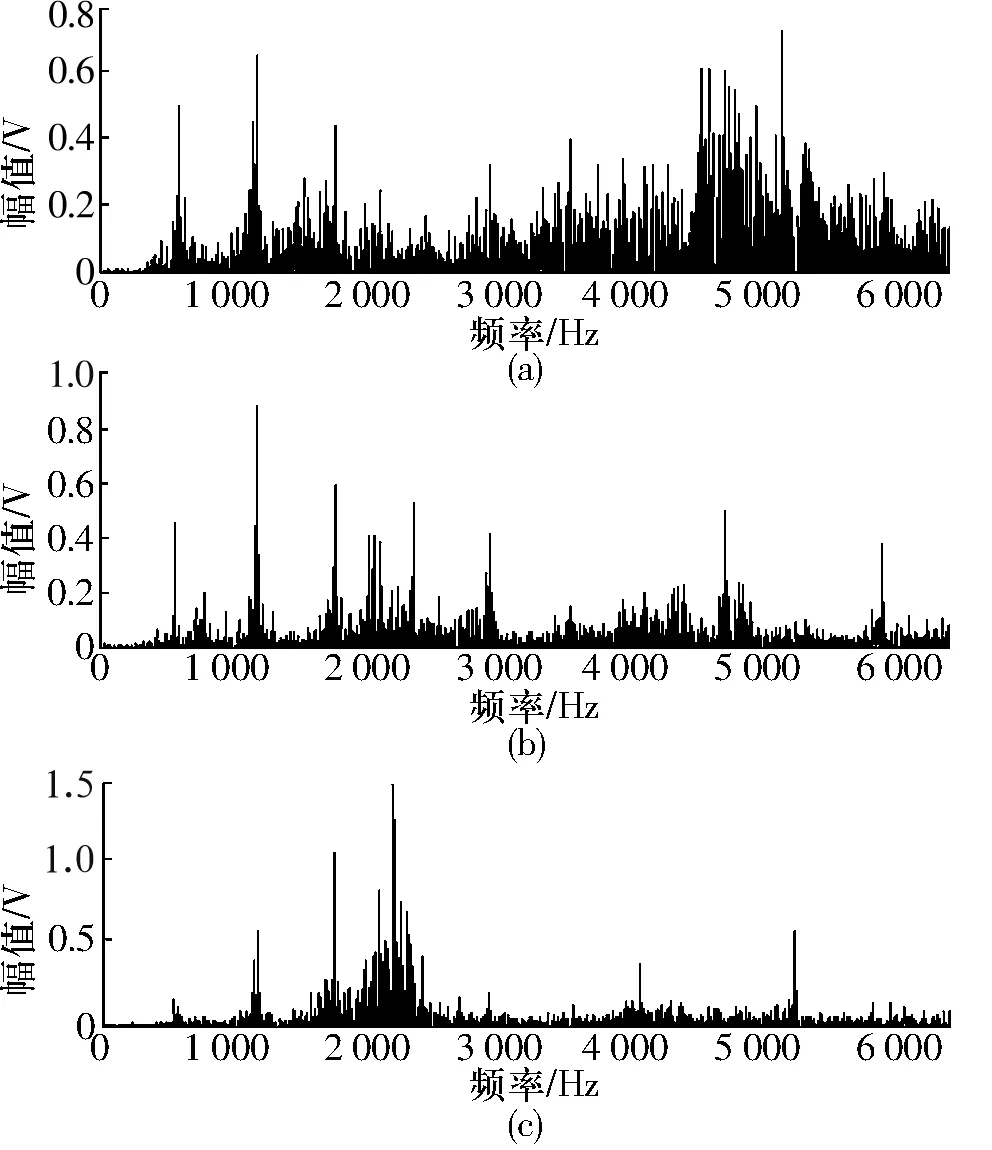
图4 3路传感器采集信号的频谱图

构造Fourier字典、Dirac字典和基于8阶消失矩Symlet小波字典，分别用以匹配振动信号中的简谐振动、冲击和其他瞬态振动现象，采用GMCA算法对采集的3路振动信号进行盲分离，图5分别为分离出的3个源信号的频谱图。

图5 GMCA分解结果

从图5a中能看出94 Hz和188 Hz的频率成分，这与滚动体故障特征频率(94.2 Hz)及二次谐波(188.4 Hz)接近，由此可认为滚动体故障被有效地分离出来；从图5b中能看出72 Hz和144 Hz的频率成分，这与外圈故障特征频率(71.6 Hz)及二次谐波(153.2 Hz)接近，由此可认为外圈故障被有效地分离出来；从图5c中能看出108 Hz和216 Hz的频率成分，这与内圈故障特征频率(108.4 Hz)及二次谐波(216.8 Hz)接近，其他频率幅值成分较小，由此可认为内圈故障被分离出来。经上述分析得出，上文提出的算法能较好地分离出滚动轴承的故障特征。