模糊数排序的指数方法

曾繁慧，曹 俊

(辽宁工程技术大学理学院，辽宁阜新123000)

0 引言

模糊数的概念由Jain[1]和Dubois[2]提出。为了比较模糊数的大小，需要引入模糊数的排序指标。1998年，Cheng[3]在Murakami，Maeda和Mamura[4]的基础上首次提出了模糊数的质心这一概念，并用模糊数的质心到原点的距离作为排序指标进行排序。2002年，Chu和Tsao[5]对模糊数质心的定义作了改进，并以质心到两坐标轴距离的乘积作为排序指标。2006年，Wang[7]又对模糊数质心的定义进行了合理改进。本文基于模糊数的质心指标，给出了一种模糊数排序的指数方法。

1 基本概念

定义1[6]论域X到[0,1]闭区间上的任意映射μA:X→[0,1]都确定 X上的一个模糊集 A，μA(x)称为A的隶属函数，μA(x)称为x对A的隶属度。为了方便起见，记论域X上的模糊集全体为F(X)；若模糊集A的隶属函数μA(x)仅取0和1，则模糊集为普通集。记论域X上的普通集全体为P(X)。

定义2[2]若模糊数A的隶属函数为

定义 3[7]模糊数 A 的质心为

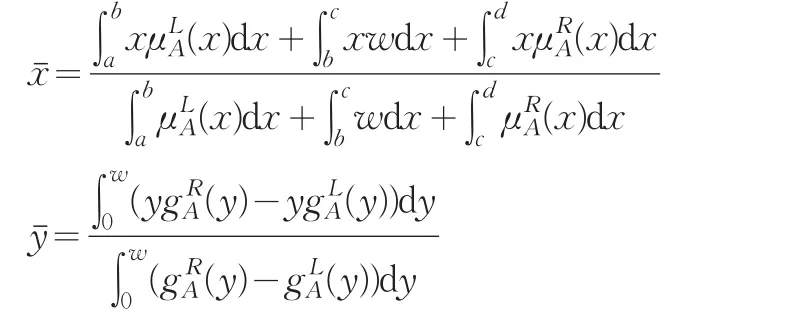
2 模糊数排序的指数方法

根据以上定义，提出模糊数的指数排序指标

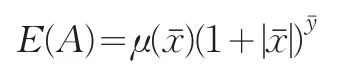
其中

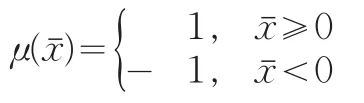
设有两个模糊数A和B，可分别计算E(A)和E(B)，其排序方法如下：

若E(A)＜E(B)，则 A＜B；

若 E(A)=E(B)，则 A=B；

若E(A)＞E(B)，则 A＞B。

新的排序指标可以同时对多个模糊数进行排序，且这个指标满足模糊数排序的常见性质[8]：

序关系的完全性，即A≥B与A≤B至少有一者成立；

序关系的传递性，即A≥B且B≥C，则有A≥C。

不相关模糊数的独立性，即在{A,B}中有A≥B，则在{A,B,C}中仍有A≥B。

3 算例分析

我们通过算例分析来说明方法的有效性。

例1比较下列模糊数：A1=(10,13,20;1)，A2=(10,17,20;0.2)，它们的隶属函数图像如图1所示。

图1 隶属函数图像

一般的，我们认为 A1＞A2，但是如果按照Cheng[3]和Wang[10]的方法却能得到A1＜A2的排序结果，显然这两种方法是有缺陷的。按照本文的排序方法可以得到A1＞A2，与直观相符。

例2比较下列模糊数大小：A1=(3,5,7;1)，A2=(3,5,7;0.8)，B1=(5,7,9,10;1)，B2=(6,7,9,10;0.6)，B3=(7,8,9,10;0.4)，它们的隶属函数图像如图2所示。

图2 隶属函数图像

利用本文所提出的方法，求得模糊数A1，A2,B1，B2，B3的排序结果为 B1＞B2＞A1＞A2＞B3。文献[9]认为B1＞A1＞B2＞A2=B3，并没有区分出A2与B3的优劣；而利用文献[10]提出的方法，得到了 B3＞B2＞B1＞A1＞A2的排序结果，由于B1的峰值高于B2的峰值，所以直观上应有B1＞B2。

4 结束语

本文基于模糊数的质心指标，给出了一种模糊数排序的指数方法。这种排序方法可以通过简单的计算实现对模糊数进行排序，并且在一定程度上克服了现有一些模糊数排序方法的缺陷，因而为决策者提供了一种新的参考。

[1]Jain R.A Procedure for Multi-aspect Decision Making Using Fuzzy Sets[J].International Journal of Systems Science,1978，（8）.

[2]Dubois D.Operations on Fuzzy numbers[J].International Journal of Systems Science,1978，（9）.

[3]C.H.Cheng.A New Approach for Ranking Fuzzy Numbers by Distance Method[J].Fuzzy Sets and Systems,1998，（95）.

[4]S Murakami,S maeda，S Imamura.Fuzzy Decision Analysis on the Development of Centralized Regional,Energy Contral System[A].ICFA Syrup on Fuzzy Infrom[Z].Knowledge Representation and Decision Anal,1983.

[5]T.C.Chu，C.T.Tsao.Ranking Fuzzy Numbers with An Area between the Centroid Point and Original Point[J].Comput.Maths,2002,(43).

[6]Yang Lunbiao,Gao Yingyi.Fuzzy Mathematic Theory and Application[M].Guangzhou:South China University of Technology Press,2005.

[7]Wang Yingming,Yang Jianbo,Xu Dongling,etal.On the Centroids of Fuzzy Number[J].Fuzzy Sets and Systems,2006,(157).

[8]Wang Xuzhu,Shan Jing.An Overview of Ranking Fuzzy Quantities[J].Fuzzy Systems and Mathematics,2002,(16).

[9]B.Asady,A.Zendehnam.Ranking Fuzzy Numbers by Distence Minimization[J].Aplied.Mathematical.Modelling,2007,31(11).

[10]Y.J.Wang,S.H.Lee.The Revised Method of Ranking Fuzzy Numbers with an Area between the Centroid and Original Points[J].Computers and Mathematics with Applications,2008,(55).