混合磁悬浮系统的H∞控制器设计

乔 芳，林小玲

(上海大学，上海200072)

0 引 言

近年来，磁悬浮技术被广泛地用于各种实际的应用领域。但由于磁悬浮系统中存在着许多不确定性因素，因此强鲁棒控制器的设计成为新的研究热点。在众多的鲁棒控制理论中，鲁棒H∞控制被认为是鲁棒性最强的控制方法之一，鲁棒H∞控制包含了传统控制方法与现代控制方法的优点，有很强的鲁棒性及抗干扰能力，但是在进行设计时需要根据实际系统合理地选择加权函数，而鲁棒稳定性和鲁棒性能的加权函数的选择却依赖于设计者的经验，至今无规律可循［1－4］。

本文针对混合磁悬浮系统，设计了H∞控制器，其仿真结果表明系统具有很好的稳定性和鲁棒性。

1 混合磁悬浮控制系统的模型

1.1 控制系统结构

混合磁悬浮控制系统的结构图如图1所示，此系统由永磁体、电磁铁、线圈、电流及位置传感器、控制器、功放及悬浮体等部分构成。永磁铁产生的磁场作为系统的偏置磁场，电磁铁线圈通以驱动电流后产生的磁场作为系统的控制磁场。系统工作时，通过获得的电流和位移反馈来控制线圈电流的大小和方向，以达到控制电磁力的大小和方向，从而使电磁力与悬浮体的重力平衡，最终使系统稳定。

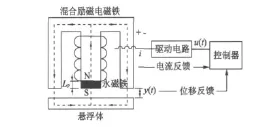
图1 混合磁悬浮实验系统结构

1.2 混合磁悬浮系统的数学模型

对图1的混合磁悬浮系统中的混合励磁电磁铁做如下假定:

(1)磁路中铁磁材料的磁导率无穷大，磁势均匀地分布在气隙和永磁铁上;

(2)忽略电磁线圈和永磁铁的漏磁通;

(3)假定悬浮体作用面的刚度系数无穷大，不考虑悬浮体本身的弹性振动和动态形变，其受力仅为竖直方向上的磁吸力、重力和外界扰动力;

对如图1所示的混合磁悬浮系统建立线圈电压平衡方程和悬浮物垂直方向运动方程，所得方程为非线性方程，难以精确地求出方程解。采用传统基于标称点线性化模型设计方法，可得线性化方程组:

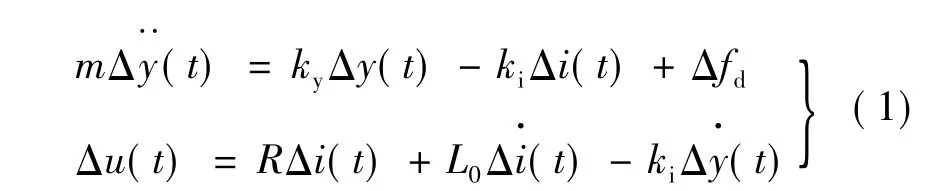
式中:m为悬浮质量;fd为外部干扰力;Δu、Δi分别为电磁铁电压和电流相对平衡点的增量;ky为气隙y(t)变化单位值时，磁力的变化值;ki为线圈电流i(t)变化单位值时，磁力的变化值;L0为混合磁铁在平衡点处的电感。

对式(1)进行Laplace变换，可得:

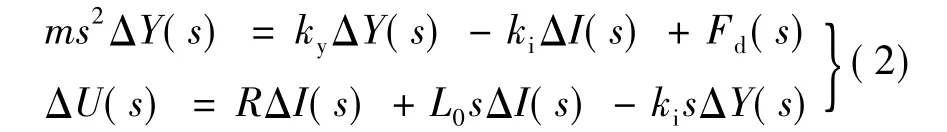
本文采用电流控制模型，将悬浮气隙作为电流的函数，驱动环节视为跟随性能很好的电流源，由式(2)可得系统电流控制模型:

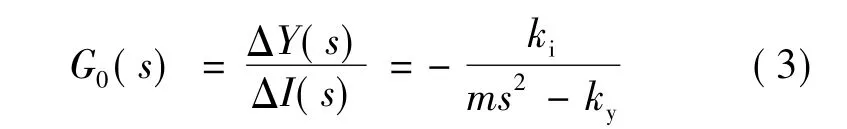
该系统，m=1.225 kg，平衡位置取为 y=17 mm，平衡时静态电流i0=0。由此得系统的开环传递函数:

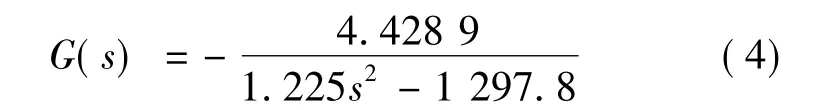
由此得出，开环控制时此系统有一个极点位于复平面的右半平面，即开环系统控制时是不能达到稳定的，须引入反馈控制。

2 鲁棒H∞控制器设计

2.1 鲁棒H∞控制器设计分析

H∞控制器设计是一种依赖于模型的设计方法。进行H∞控制器的设计时，首先必须建立被控对象的数学模型，然后将该模型化为H∞标准控制问题所对应的增广被控对象的模型，最后，按照H∞标准控制问题的求解方法设计控制器。在实际应用中，许多控制问题均可转化成鲁棒H∞控制问题，如鲁棒稳定性、跟踪、干扰抑制等。H∞控制的目的就是要求使得系统的外界干扰到系统的可控输出在范数意义下控制在一定的水平。实际应用中，标准H∞问题即是在系统中以加权函数去影响闭环系统的某些性能，使得设计的控制器具有鲁棒性。如图2所示。

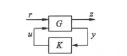
图2 标准H∞控制问题

图2中，r为输入，u为控制输入，z为评价输出(即可控输出)，y为系统输出，K为控制器，G为广义受控对象。广义受控对象是在被控对象基础上进行加权增广得到的，即G不仅包含实际系统的模型函数，还包含为满足系统性能而引入的加权函数。

而H∞混合灵敏度优化法恰是一种多变量鲁棒控制器设计的有效方法，此方法是指闭环控制系统性能可以通过合理地选取权函数来达到，灵敏度函数表示了由干扰输入d到系统输出y的传递函数，同时也是从参考输入r到系统偏差e的传递函数，它反映了系统对输出端扰动的抑制性能，是一项重要的性能指标。显然，灵敏度越小越好。进行控制器设计时，为了保证控制系统的鲁棒性，一般都将鲁棒H∞控制问题转化为混合灵敏度问题进行计算，控制系统如图3所示［3］。

图3 混合灵敏度问题的标准框架

图3中:G(s)为开环传递函数;K(s)为H∞控制器;r、e、u、d、z、y 及 n 分别为输入、误差信号、控制量、干扰量、评价系统输出、系统输出及噪声。W1(s)、W2(s)和W3(s)分别为系统的性能权、控制器输出权，鲁棒权。它们分别决定了系统的抗干扰能力、参数摄动的范数界和系统的鲁棒稳定性。从参考输入r到e，u和y的闭环传递函数分别为:

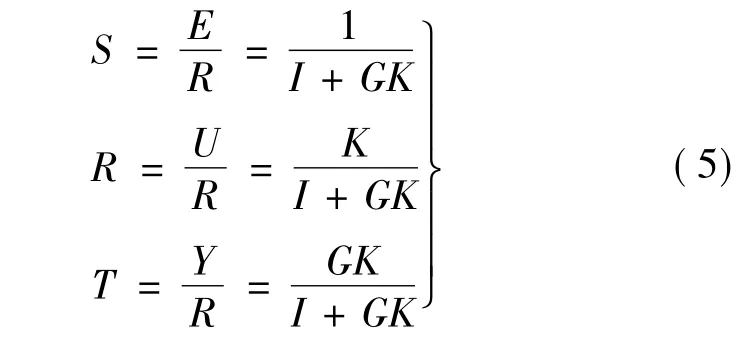
式中:S和T分别为控制系统的灵敏度函数和补灵敏度函数。对于混合磁悬浮控制系统，将预先设定的悬浮体的平衡位置作为输入量，r和u作为控制器量，误差信号和悬浮体的偏移位置量作为广义被控对象的输出。对于图3的控制系统的鲁棒H∞混合灵敏度问题的标准框架:

其中，广义受控对象及其状态表达式:

由式(6)构成的闭环传递函数阵:

混合磁悬浮控制系统的鲁棒H∞混合灵敏度设计即寻找有理函数控制器K，使闭环控制系统稳定，且‖P‖∞最小。设最小值为γ0，但是通常比较难找到准确解，所以一般采用准最优解，即找一个稳定的控制器 K，使‖P‖∞=γ≥γ0。故有:

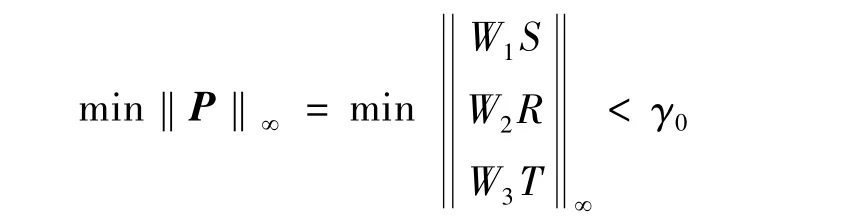
或

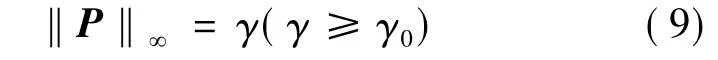
这就使混合磁悬浮控制系统的控制器设计问题转换成了混合灵敏度控制的设计问题。

2.2 权函数阵的设计选择

H∞控制器的设计实际上是对灵敏度函数S、R和T的加权函数W1(s)、W2(s)和W3(s)的选择过程。加权函数选择合适与否决定了系统性能的优劣。本文加权函数的选取遵循如下规则［3－7］:

(1)遵循鲁棒控制第一定理

灵敏度加权函数W1(s)应满足:

补灵敏度函数T是系统输出与参考输入之间的传递函数矩阵，补灵敏度加权函数W3(jω)应满足:［T(jω)］是 T(jω)的奇异值，W3(s)是系统所期望的复合干扰的幅值。

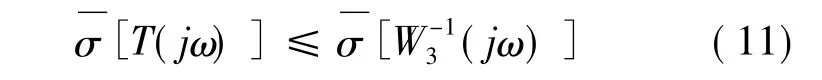
(2)阶次要求

在满足鲁棒第一定理不等式(10)和式(11)的条件下，应尽量选择低阶次的权函数，通常选择一阶函数。

(3)W1、W2的截止频率

W1截止频率应选择在低频段，以保证控制系统有良好的低频跟踪能力。W3截止频率应该向高频段偏移，从而过滤掉外界的复合干扰。

(4)W1、W3的幅值特性

在保证整个控制系统稳定的前提下，灵敏度加权因子W1要求在低频段增益大，高频段的增益为零即可。补灵敏度加权因子W3在低频段要求增益很小，在高频段增益要大。

依据以上设计原则，经过反复实验本文选取加权函数如下:

通过Matlab鲁棒控制工具箱，结合式(4)和式(12)，最终求得到系统H∞控制器:

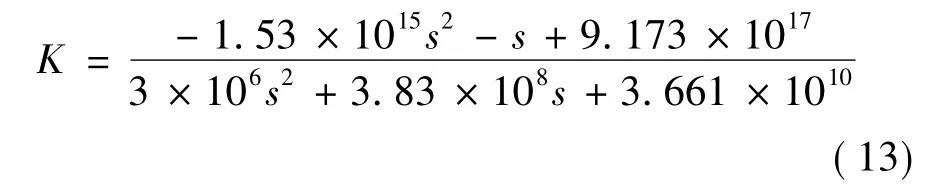
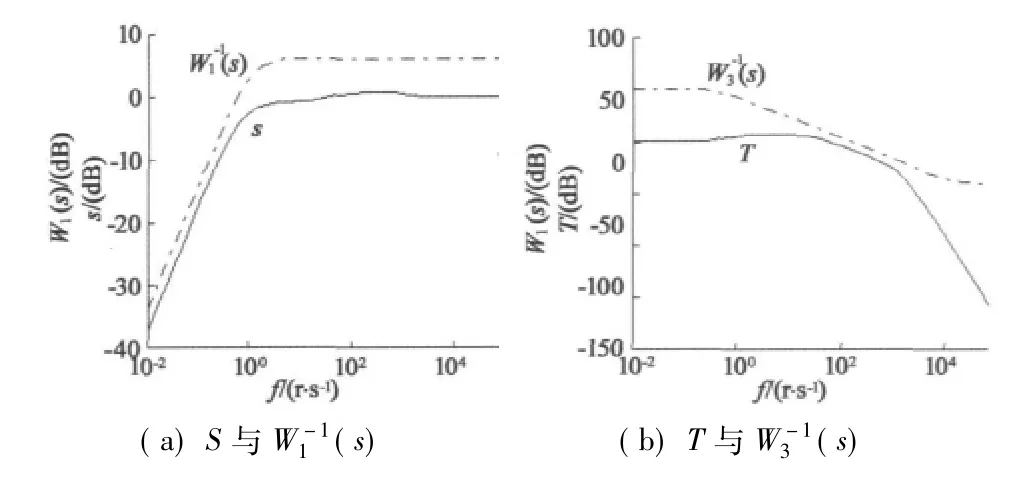
图4 奇异值曲线

3 系统仿真

根据以上分析，借助Matlab的 Simulink工具箱，建立混合磁悬浮控制系统的仿真模型，控制器K采用S－Function编写，仿真模型如图5所示。

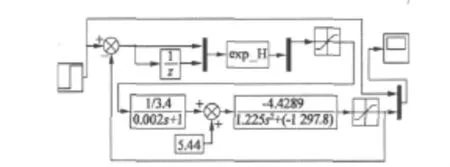
图5 磁悬浮系统的H∞控制器仿真框图

将H∞控制器用于混合磁悬浮控制系统的仿真，与传统的PID控制器仿真进行比较，仿真结果如图6所示。

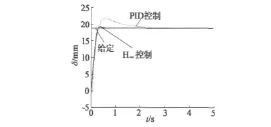
图6 H∞控制器控制时的仿真波形

从图6中可以看出，采用PID控制，系统的超调量约为19%，系统的稳定时间约在2.5 s，而采用H∞控制，系统的超调量不到5%，稳定时间在0.6 s左右，另外系统的上升时间也比PID控制的要小。可见，H∞控制的系统性能明显优于PID控制。

4 结 语

本文对现有的混合磁悬浮控制系统，设计了混合磁悬浮系统的H∞控制器，并进行了仿真研究，且与传统的PID控制方法进行了仿真比较。结果表明:基于H∞的鲁棒控制器明显优于传统PID控制器的控制性能，这为今后对鲁棒H∞控制方法的研究与设计起到了很好的参考借鉴作用。

［1］ Yi J H，Park K H，Kim S H，et al.Robust force control for a magnetically levitated Manipulator using flux density measurement［J］.Control Engineering Practice，1996，4(7):957 －965.

［2］ Uchiyama Y，Mukai M，Fujita M.Robust acceleration control of electrodynamics＇shaker using μ － synthesis［C］//Proceedings of the 44th IEEE Conference on Decision and Control.Seville，2005:6170－6175.

［3］ Chen B，Li Y，Zhang G，et al.H∞Robust Control of a Novel Magnetic Levitation Stage［C］//Proceedings of the 2006 IEEE International Conference on and Robotics Biomimetics.2006.

［4］ 赵雪山.永磁偏置径向轴向磁轴承H控制系统的研究［D］.南京航空航天大学，2004，34 －39.

［5］ 赵雪山，王成华.永磁偏置径向轴向磁轴承的H∞控制系统的研究［D］.南京航空航天大学，2004:24～39.

［6］ 李群明，朱伶，徐震.磁悬浮球的鲁棒控制器设计［J］.中南大学学报(自然科学版)，2007，38(5):923－925.