基于舰船振动信号激励下压电智能梁振动主动控制

宋媚婷 洪 明 崔洪宇

大连理工大学 运载工程与力学学部 船舶工程学院，辽宁 大连116024

基于舰船振动信号激励下压电智能梁振动主动控制

宋媚婷 洪 明 崔洪宇

大连理工大学 运载工程与力学学部 船舶工程学院，辽宁 大连116024

为研究舰船结构振动主动控制有效方法，采用线性二次型独立模态空间控制法设计控制器，对舰船振动信号激励下压电智能梁的振动进行主动控制。基于Hamilton原理建立压电智能结构的有限元模型，并利用精细积分法计算前3阶模态的位移响应。编制了相应的计算机程序，对舰船振动信号激励下梁结构的振动进行主动控制数值仿真。由仿真结果可见，控制可以有效地实现，为舰船结构振动主动控制提供理论基础。

智能结构；振动控制；精细积分

1 引言

舰船主要受到螺旋桨、主机、波浪和风等激励源的作用，激励源的频谱表现为强线谱和宽频谱的叠加。舰船的实际激励信号很难确定，但通过实测得到的实船振动响应信号具有宽频和强线谱叠加的特征，为此本文应用实测得到的振动响应信号代替舰船的激励信号，探讨舰船振动信号激励下柔性结构振动主动控制有效方法，为实现舰船结构振动主动控制提供理论基础。

压电智能材料已经被广泛应用到结构振动主动控制中，Stavroulakis 等人［1］基于 Hamilton 原理建立上下表面分别粘贴压电片的细长梁有限元模型，分别采用最优控制和H2鲁棒控制方法抑制细长梁在风载荷下的振动。 Kumar和 Narayanan［2］基于Euler－Bernoulli梁理论建立梁有限元模型，采用线性二次型调节器方法设计控制器，并针对3种不同边界条件的梁，根据遗传算法优化了压电片的位置。Kapuria和Yasin［3］采用独立模态空间控制和线性二次型最优控制相结合的方法，对复合材料梁振动进行了控制，这种方法近年来也被研究与应用，它可实现对所需控制的模态进行独立的控制，不影响其他未控的模态。

基于压电作动方式，本文以压电陶瓷作为传感器和作动器，基于压电层合单元有限元模型，模拟压电层合结构机电耦合行为。舰船振动主动控制技术主要研究如何有效抑制低频振动，提高舰船隐蔽性和安全性。由于螺旋桨和主机激励引起舰船结构的有害振动主要是低频振动，且低阶模态对舰船振动系统的影响较大，因此，采用线性二次型独立模态空间控制方法应该有很大的优越性。本文编制了相应的计算机程序，对舰船振动信号激励下梁结构进行振动主动控制数值仿真，证明该方法的有效性。

2 线性二次型独立模态空间控制

线性二次型独立模态空间控制法就是将独立模态空间控制（IMSC）与线性二次型（LQR）最优控制相结合的新的控制方法。它的主要思想是对振动系统中影响较大的1阶或几阶振动模态进行控制，从而使整个系统振动响应得到抑制。由于它可实现对所需控制的模态进行独立控制而不影响其他模态，设计简单，在一定程度上能抑制控制溢出，因此，目前已成为一种在模态控制领域中被广泛应用的方法。

2.1 压电层合结构有限元模型的建立

压电层合结构是在结构表面粘贴或内部嵌入压电片形成的层合结构，它已经被广泛的应用到结构振动主动控制中。由于压电层对结构固有特性有很大影响，因此有必要采用压电层合结构有限元模型，分析其机电耦合行为。

本文采用4节点四边形壳单元，每个节点有5个广义位移自由度，每个单元另外加上2个电势自由度，分别为压电驱动器的电势自由度和压电传感器的电势自由度。单元模型如图1所示。

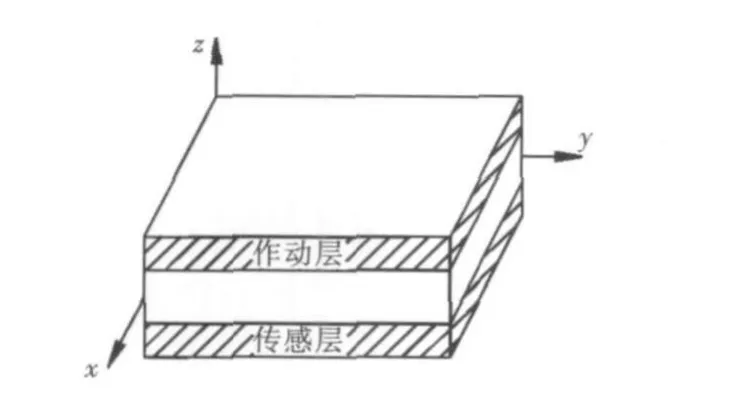
图1 压电层合单元模型Fig.1 Model of piezoelectric composite element

对于压电薄层，Tiersten［4］给出其本构方程的形式为：

式中，σ和ε分别为压电层的应力和应变矢量；Q为压电层弹性矩阵；e为压电应力常数矩阵；E为电场矢量；D为电位移矢量；P为介电常数矩阵。

将上式改写为如下形式：

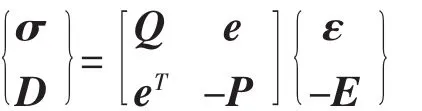
记作：

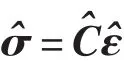
由于压电层沿厚度方向极化，所以：

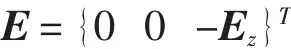
式中，Ez＝－φ／t；φ为压电层上下表面的电势差。

采用双线性4节点四边形等参单元，形函数为 Ni＝ （1 ＋ ξξi）（1＋ ηηi）／4，i＝1，2，3，4。 单元内任意点位移为：

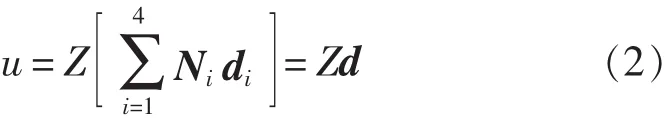
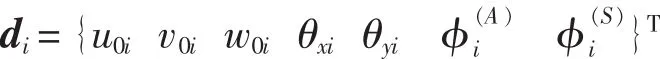
含有n个压电层的层合板／壳单元的位移与应变关系可以写为：

记作：

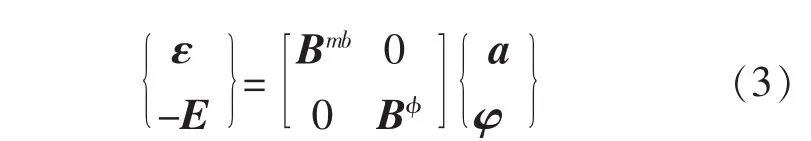
根据Hamilton原理，可以得到压电层合单元的刚度阵和质量阵分别为：

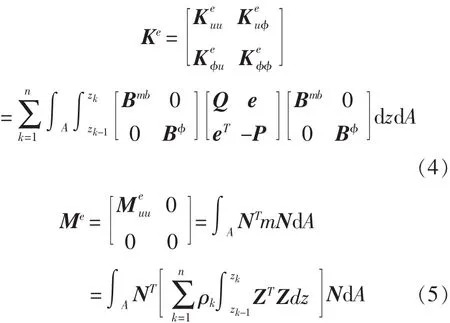
将压电电势分为传感部分 φ（S）和作动部分 φ（A），且传感层外加电势为零，系统运动方程可写为［5-12］：

式中，Fext（t）为外部激励力；Q（A）为作动器作用电势的等效力。

将上式展开整理，并加上阻尼项，得系统有阻尼运动方程：

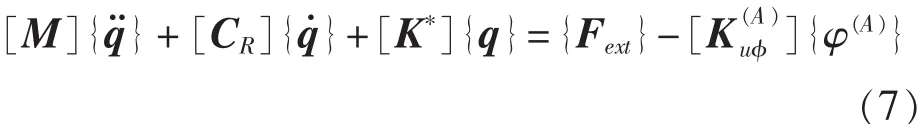
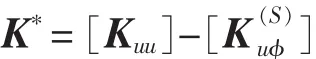
2.2 线性二次型独立模态空间控制法

本文采用线性二次型独立模态空间控制方法进行研究。首先，将式（7）转化到模态空间，即将物理坐标结点位移｛q｝用前n阶低频模态对应的模态坐标｛ξ｝表示：

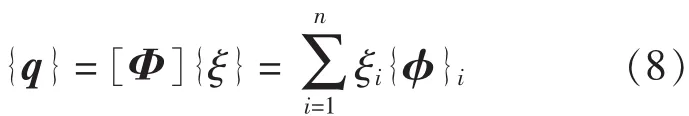
式中，［Φ］是正则振型矩阵。

将式（8）代入式（7）中，左乘［Φ］T则有：

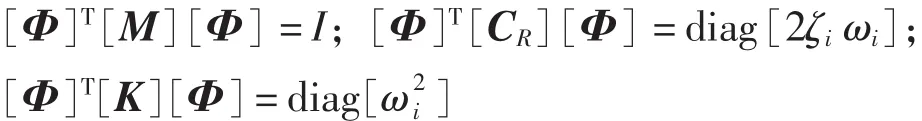
可将式（1）在模态空间解耦，得相应的运动方程：

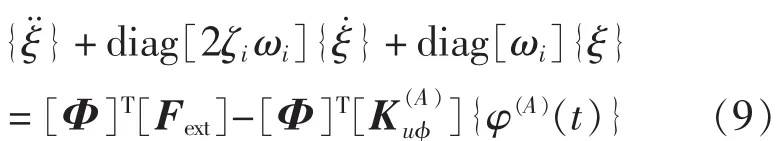
从解耦的式（9）可以看出，对于独立模态空间控制，可得到各阶模态振动控制方程，本文只取前3阶模态。对应每阶模态，采用精细积分法由式（9）可求出各阶模态的响应。

其次，将式（9）转化到状态空间中，得

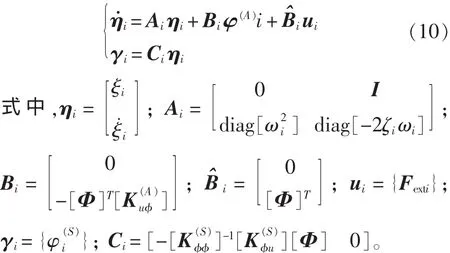
解状态空间式（10）即可得到前3阶模态响应。

最后，由线性二次型最优控制律，得反馈控制电势应满足：

式中，GAi是模态控制增益；ηi为模态坐标向量，同式（10）。

目标函数选为传感器输出以及作动器控制电势的二次加权和：

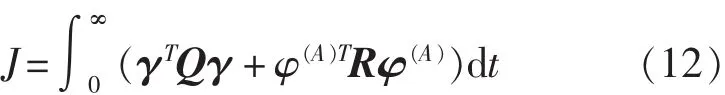
式中，Q权系数矩阵为半正定对称阵。通常R为单位阵，调整Q即可。γ同式（10）。

优化控制增益为：

式中，Pi满足Riccati方程：

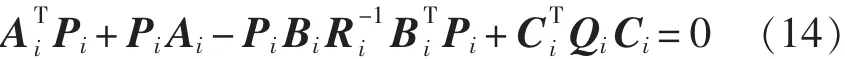
将式（11）和式（13）代入式（10），即可得到利用线性二次型独立模态空间控制方法进行控制的状态空间方程为：

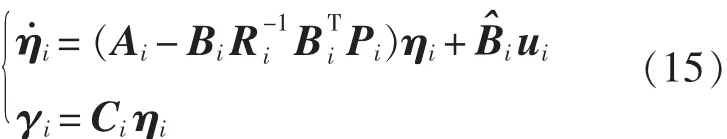
3 数值算例

基于以上的理论，本文采用FORTRAN语言编程，采用精细积分法的HPD－L格式计算结构在舰船振动信号激励下前3阶模态振动响应。采用精细积分法求解 Riccati方程式（14），再由式（13）求得控制增益。最后求解式（15），即得控制后的模态响应。

本文以某一悬臂梁为例，如图2所示。梁的尺寸为600 mm×50 mm×10 mm，上下由性质相同的压电层全部覆盖，压电层厚度为2 mm，压电层和中间层的材料特性如表1所示。将压电层合悬臂梁划分为12个单元，其单元编号及节点编号如图3所示。

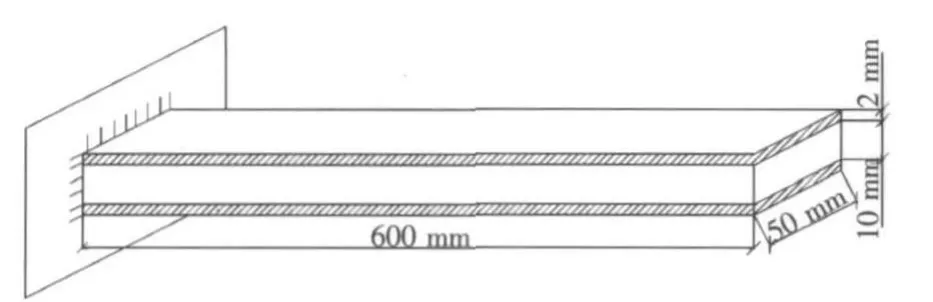
图2 压电层合悬臂梁Fig.2 Finite element model of piezoelectric laminated cantilever

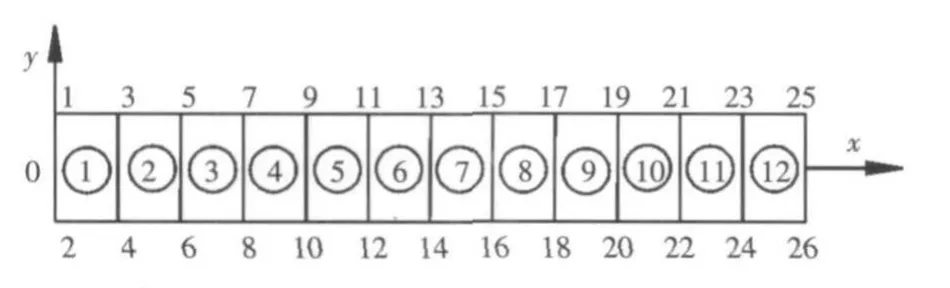
图3 单元编号及节点编号Fig.3 Node serial numbers and element serial numbers

表1 材料特性Tab.1 Material properties

在悬臂梁自由端施加激励，此激励来源于某船航行时实测的振动响应时域信号，激励如图4所示。由于舰船的激励信号很难确定，为此本文通过计算此激励作用下梁的振动响应，来模拟舰船振动响应，以此来研究舰船结构振动主动控制有效方法。

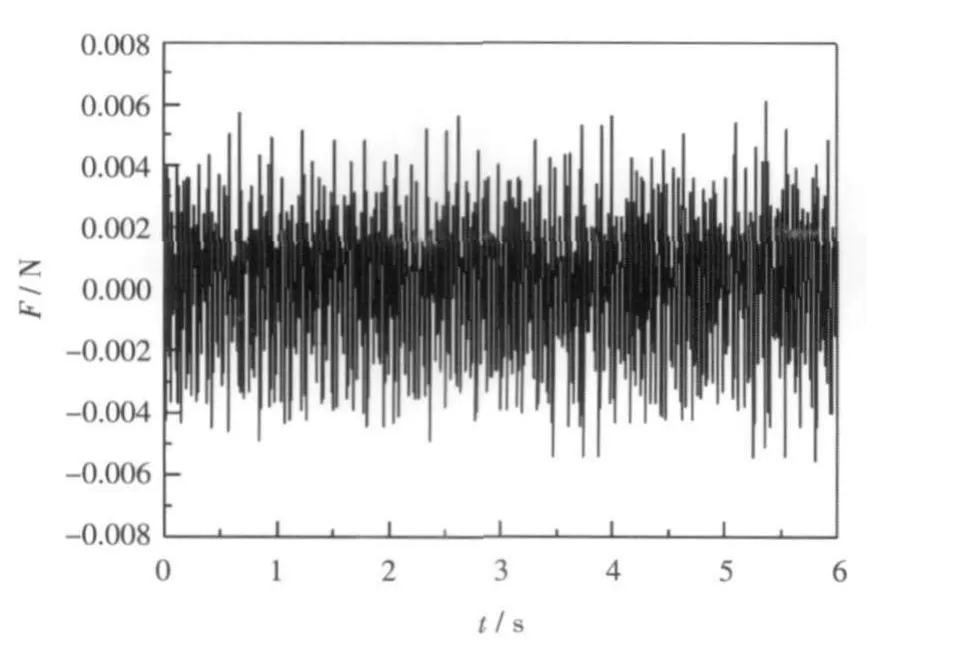
图4 激励时域曲线Fig.4 Curve of exciting force in time domain

本文选用 Rayleigh 阻尼比 α＝3 和 β＝1×10－4。初始状态为静止，积分步长为0.005 s。在控制过程中，取权系数Q＝1×1014。由式（13）所得的前3阶模态控制增益分别为：

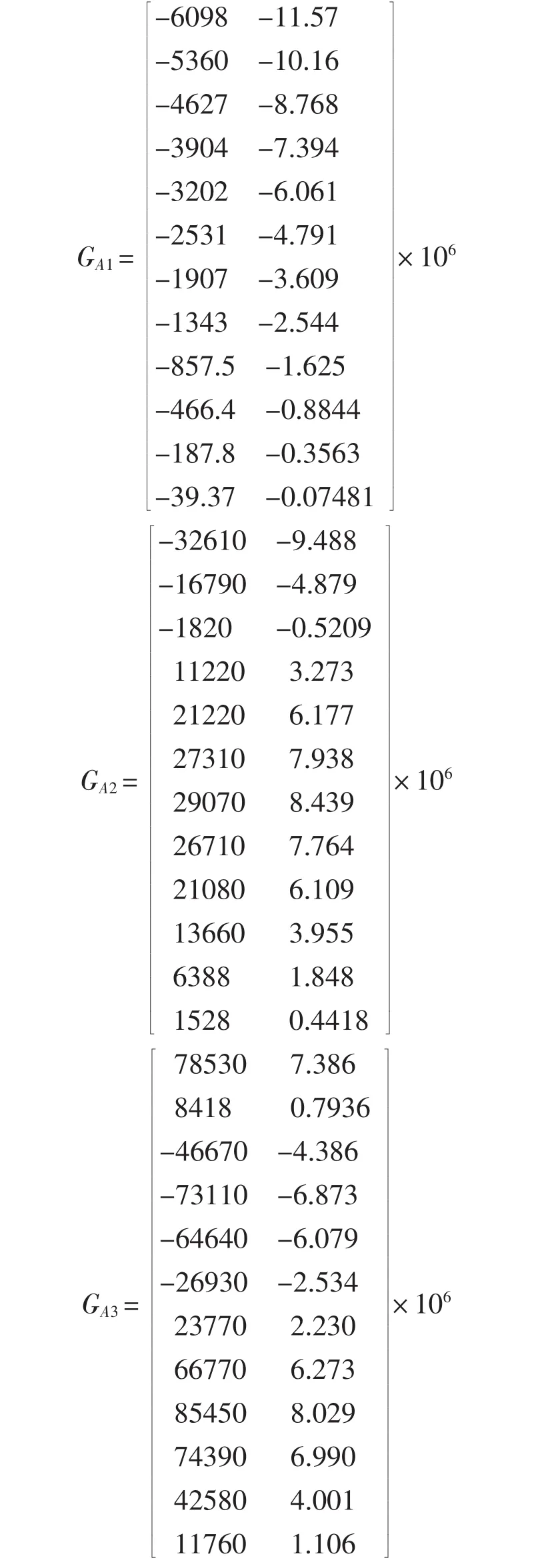
由精细积分方法的HPD＿L格式求出的悬臂梁自由端控制前后前3阶模态位移响应曲线分别如图5、图7和图9所示。由于固定端应变比较大，所需的控制电势较大，因此输出一号单元前3阶模态的控制电势（由式（11）求得）如图6、图8和图10所示。

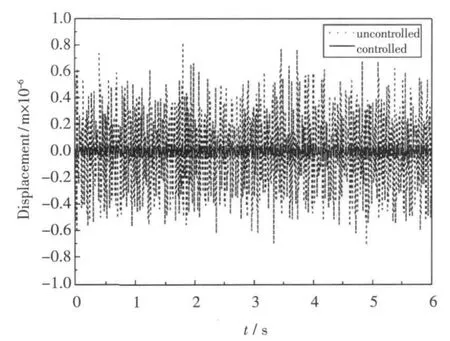
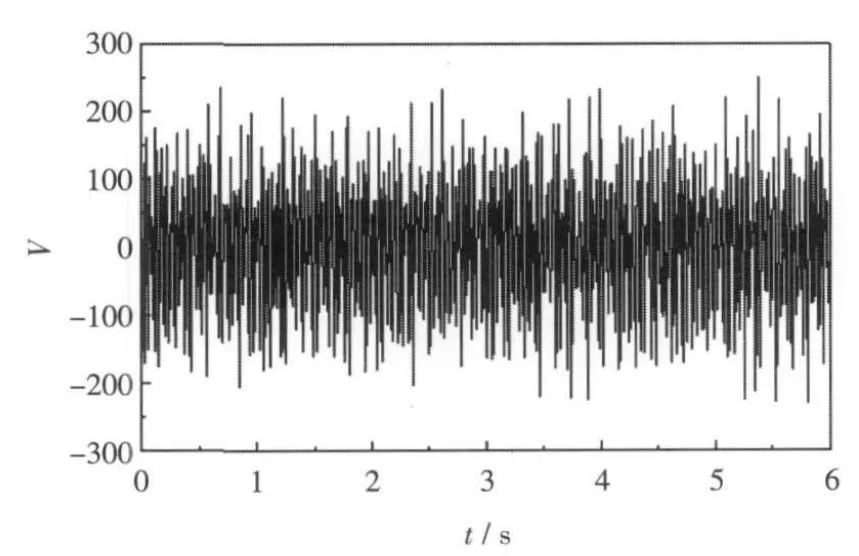
图6 1号单元作动层1阶模态控制电势Fig.6 Voltages of actuator in the first element with the first modal controlling

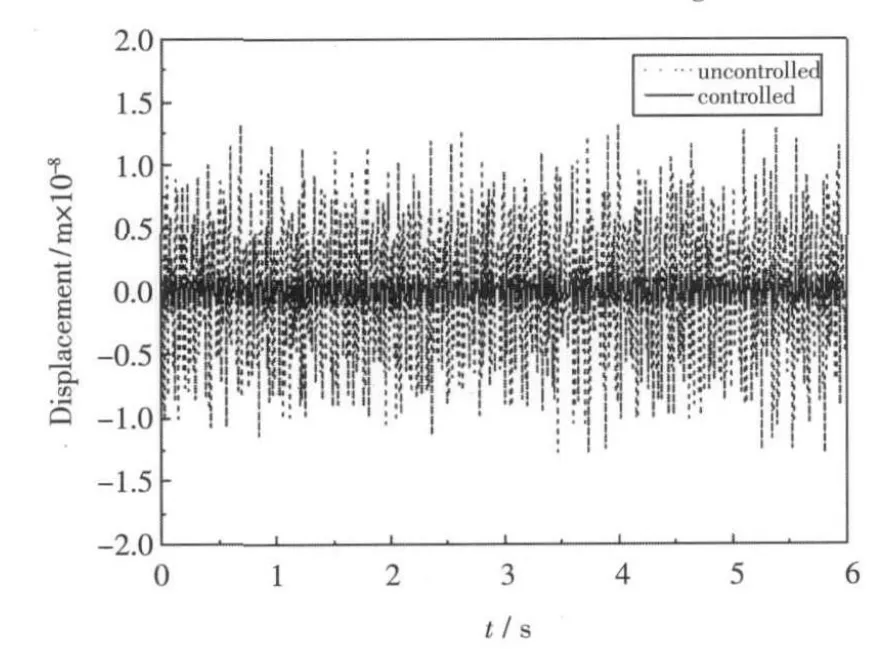
图7 悬臂梁自由端控制前后第2阶模态位移响应Fig.7 Tip second modal displacement response of the cantilever before and after control

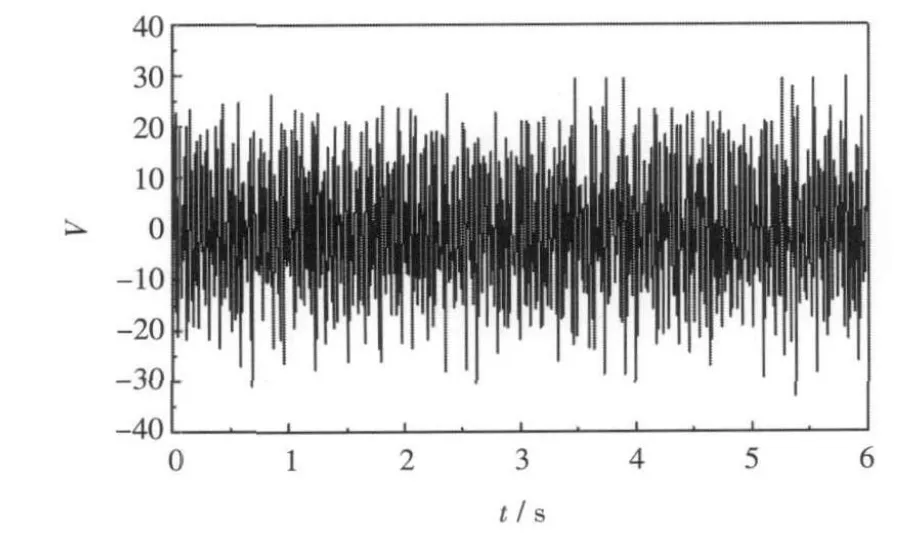
图8 1号单元作动层2阶模态控制电势Fig.8 Voltages of actuator in the first element with the second modal controlling

图10 1号单元作动层3阶模态控制电势Fig.10 Voltages of actuator in the first element with the third modal controlling

从图5～图10可以看出，经过控制后，各阶模态位移响应得到了有效地控制。为分析控制效果，分别计算前3阶模态控制前后位移响应的功率谱密度，采用Welch法估算的单边功率谱密度结果分别如图11、图12和图13所示。

从图中可以看出，控制后，前3阶模态在0～100 Hz的区间对应的功率谱密度明显减小，在此区域中的频率对应的能量明显降低，控制得以实现。

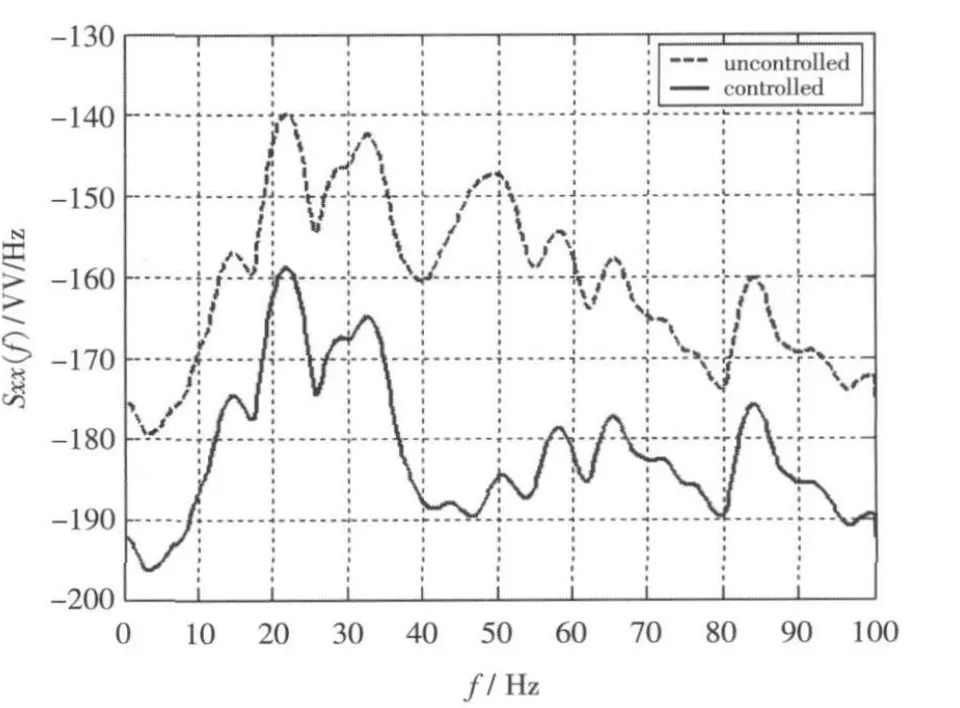
图11 1阶模态位移响应自功率谱密度Fig.11 Auto power spectral density of the first modal displacement response before and after control

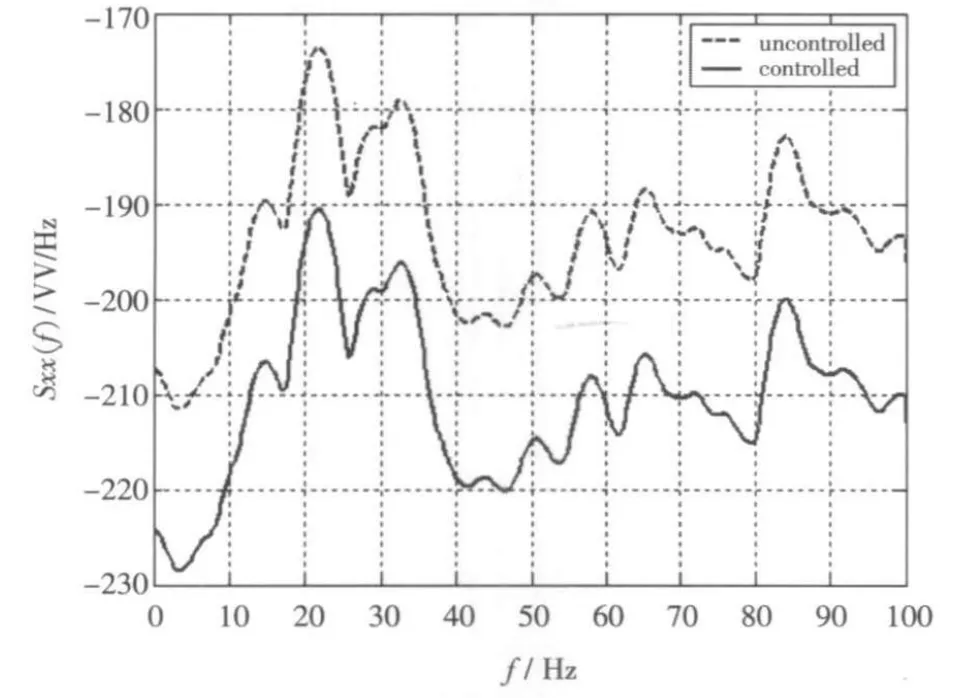
图12 2阶模态位移响应自功率谱密度Fig.12 Auto power spectral density of the second modal displacement response before and after control

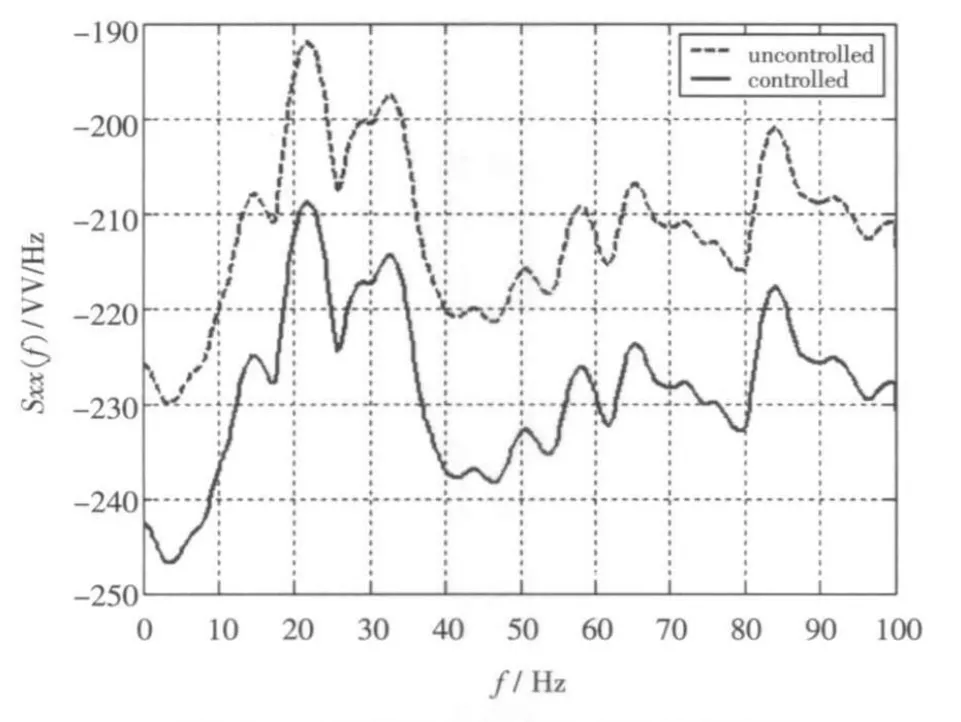
图13 3阶模态位移响应自功率谱密度Fig.13 Auto power spectral density of the third modal

4 结束语

本文采用线性二次型独立模态空间控制方法对舰船振动信号激励下压电层合梁结构的振动进行主动控制；应用基于Hamilton原理得出的压电层合单元模型模拟压电层合结构的机电耦合行为；采用精细积分法计算舰船振动信号激励下梁结构的振动响应。从数值算例仿真结果可以看出，应用本文的控制方法控制后，梁结构各阶模态位移响应的自功率谱密度减小，控制得以实现。本文的控制方法能有效地控制舰船振动信号激励下梁结构振动响应，此方法为进行舰船结构振动主动控制提供理论基础。

［1］STAVROULAKIS G E，FOUTSITZI G，HADJIGEORGIOU E.Design and robust optimal control of smart beams with application on vibrations suppression［J］.Advances in Engineering Software， 2005， 36 （11/12）： 806-813.

［2］KUMAR K R，NARAYANAN S.Active vibration control of beams with optimal placement of piezoelectric sensor／actuator pairs ［J］.Smart Materials and Structures，2008，17（5）：1-15.

［3］KAPURIA S，YASIN M Y.Active vibration control of piezoelectric laminated beams with electroded actuators and sensors using an efficient finite element involving an electric node［J］.Smart Materials and Structures，2010，19（4）：19-33.

［4］TIERSTEN H F.Linear piezoelectric plate vibrations［M］.New York：Plenum Press，1969.

［5］SIMOES M.Active control of adaptive laminated structures with bonded piezoelectric sensors and actuators［J］.Computers and Structures，2004，82（17-19）：1349-1358.

［6］SONG G，GU H.Active vibration suppression of a smart flexible beam using a sliding mode based controller［J］.Journal of Vibration and Control，2007，13（8）：1095-1107.

［7］WANG W Y，WEI Y J，WANG C.Modeling and optimal vibration control of conical shell with piezoelectric actutors［J］.High Technology Letters，2008，14（4）：418-422.

［8］SONG G，QIAO P Z，BINIENDA W K，et al.Active vibration damping of composite beam using smart sensors and actuators［J］.Journal of Aerospace Engineering，2002，15（3）：97-103.

［9］QIU Z C，ZHANG X M，WU H X， et al.Optimal placement and active vibration control for piezoelectric smart flexible cantilever plate［J］.Journal of Sound and Vibration，2007，301（3/5）：521-543.

［10］SIMÕES R C，VALDER S，JOHAN D H， et al.Modal active vibration control of a rotor using piezoelectric stack actuators［J］.Journal of Vibration and Control，2007，13（1）：45-64.

［11］HARARI S，RICHARD C，GAUDILLER L.New semiactive multi-modal vibration control using piezoceramic components ［J］.Journal of Intelligent Material Systems and Structures，2009，20（13）：1603-1613.

［12］SHARMA M，SINGH S P，SACHDEVA B L.Modal control of a plate using a fuzzy logic controller［J］.Smart Materials and Structures，2007，16（4）：1331-1341.

Active Vibration Control of a Piezoelectric Smart Beam Excited by the Vibration Signal of Vessel

Song Mei－ting Hong Ming Cui Hong-yu

School of Naval Architecture Engineering，Faculty of Vehicle Engineering and Mechanics，Dalian University of Technology， Dalian 116024， China

To research the effective method for active vibration control of vessel structure， an Independent Modal Space Control （IMSC）technique based on Linear Quadratic Regulator （LQR）method was adopted to design the controller， taking an active vibration control of a piezoelectric smart beam， which is under the vessel＇s vibration signal excitation.The finite element model of the piezoelectric composite structure was developed based on the Hamilton＇s principle.Furthermore the high precise direct integration method was used to calculate the displacements of first three order modes.A numerical simulation of active vibration control was performed.The results show that the control can be implemented effectively and it provides a theoretical basis for active vibration control of vessel structure.

smart structure； vibration control； high precise direct integration method

TB53

A

1673－3185（2011）06－28－06

10.3969/j.issn.1673-3185.2011.06.006

2011-05-13

国家自然科学基金项目（51079027）

宋媚婷（1987－），女，硕士研究生。研究方向：结构失效、振动和噪声机理、预报及控制。E-mail：smt19870105＠163.com

洪 明（1959－），男，教授。研究方向：结构失效、振动和噪声机理、预报及控制研究。E-mail：mhong@dlut.edu.cn