基于移动区间的GPS精密星历内插方法①

张晨艳，何秀凤，常 亮

（河海大学卫星及空间信息应用研究所，江苏 南京210098）

0 引 言

GPS精密星历由国际卫星导航服务（IGS）、美国国家大地测量局（NGS）等分析中心发布，给出了卫星在国际地球参考架（ITRF）中的三维坐标及卫星钟差，其中最终星历的精度小于5cm，可以满足高精度定位的要求［1]。GPS精密星历的数据采样间隔一般为15min，但在实际应用中，GPS接收机的采样率为30s、15s、5s，甚至更密［2－4]。因此，需要将GPS精密星历进行内插或外推以得到特定历元的GPS卫星的精密轨道。另外，几乎所有的GPS数据处理都需要对GPS精密星历进行内插或外推，无论是GPS相对定位还是精密单点定位，都需要某时刻的卫星位置才能顺利建立各个历元的观测方程［4－5]。

国内外比较常用的GPS精密星历插值方法是Lagrange多项式插值、Neville多项式插值、Chebyshev多项式拟合、Trigonometric多项式插值等方法［5]。由于这些多项式插值方法随着阶数的增加，出现精度衰减或不稳定的问题。对这一问题，本文提出了移动区间的概念，在精密星历内插的过程中，通过使被插值节点始终位于移动区间内，提高了上述多项式插值方法的精度，插值精度更加稳定。

采用移动区间的方法比较7家GPS分析中心所提供的精密星历的质量。7家提供GPS精密星历的分析中心分别是：国际GNSS服务（IGS）、美国国家大地测量局（NGS）、加拿大自然资源部（NRCan）、欧洲航天局（ESA）、喷气动力试验室（JPL）、麻省理工学院（MIT）、斯科利普斯海洋研究所（SIO），它们提供的数据产品的名称分别为：igs、ngs、emr、esa、jpl、mit、sio.然后采用数据质量较好的精密星历，利用基于移动区间的插值方法，比较随着阶数的增加、插值方法的变化插值精度的变化情况。

2 几种GPS精密星历插值方法

2.1 Lagrange多项式插值

设有n＋1个节点历元t0，t1，t2…，tn，对应的精密星历坐标某项为：x0，x1，x2…，xn，则计算相应时刻卫星坐标的n阶插值多项式为［7－11]：

利用公式（1）分别对卫星坐标的三个分量（X，Y，Z）进行插值计算，即可得到观测时刻卫星的坐标。

2.2 Neville插值

Neville插值是一种线性逐次插值，其基本思想是通过低一次多项式的组合来获得高一次插值多项式。首先求出若干个一次插值多项式的值，用一次多项式两两组合得到若干个二次插值多项式的值，利用二次多项式之间两两组合得到三次多项式得到值，依次采用迭代方式求出各插值节点的值。

设有n＋1个历元时刻t0，t1，t2…，tn对应的精密星历坐标某项为：x0，x1，x2…，xn，令Ti，0＝xi（i＝0，1，2…n），则有［8]

2.3 三角多项式（Trigonometric）插值

三角多项式插值的函数为

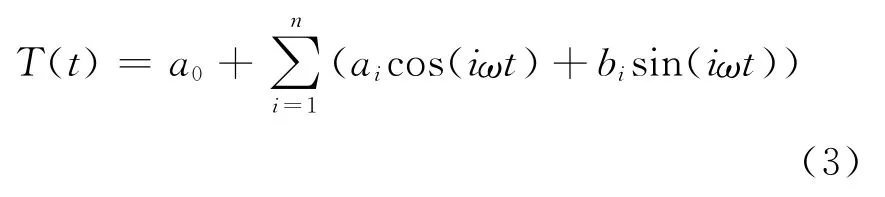
式中：t为精密星历的历元时刻；T（t）为历元t对应的卫星的坐标分量（X，Y，Z）；a0、ai、bi（i＝1，2，…，n）为待求系数；ω为特征因子。根据卫星的运动周期，对于惯性系下的轨道，ω＝2π／0.997 269 566 34.其中，0.997 269 566 34为恒星时与太阳时的比率，而对于地心地固坐标系下的轨道缩小了一倍，即ω＝2π／2×0.997 269 566 34.三角函数多项式插值中考虑了卫星坐标在两种框架下各自的周期特性［1，2，10]。

3 移动区间的精密星历插值方法

采用上述的多项式插值方法进行精密星历的内插时，随着阶数的增加，插值会发生衰减或不稳定现象。例如，Lagrange多项式插值随着阶数的增加会出现龙格（Runge）振荡现象，插值结果在端点处误差比较大，基于此提出了基于移动区间的GPS精密星历插值方法。

移动区间的定义：以一个指定大小的区间以固定的步长在二维空间中移动，移动时，即可采用某种多项式插值计算每个区间内的待插值节点对应的坐标值，此区间即称为移动区间。在GPS精密星历内插的过程中，当所有插值节点按递增或递减排列时，移动区间的选取为位于插值节点序列中间的两个插值节点构成的区间，也就是说插值节点始终位于插值范围的中心［4]。例如我们想要得到6阶多项式，每次插值需要7个节点完成插值，而被插值点始终是位于第三个到第四个点之间。第一个点到第七个点就是第一个插值区间，第三个节点到第四个节点称为移动区间，仅用来插值位于移动区间之间的被插值节点。插值区间和移动区间在该次插值过程中区间的大小始终保持不变，每次将窗口向后移动一个历元的距离，仅用来插值位于移动区间两个历元之间的被插值点［6]。

基于移动区间的精密星历内插的实现步骤如下所示：

1）移动区间的起始节点t＿start和终止节点t＿end的确定

①Trigonometric插值起始节点和终止节点的

确定：m阶插值需要2m＋2个插值节点t1，t2，…，t2m＋1，t2m＋2，所对应的坐标值为 X1，X2，…，X2m＋1，X2m＋2，设｛Xi｝单调递增（i＝1，…，2m＋1，2m＋2）。起始节点和终止节点分别为：［t＿start，t＿end]＝［tm＋1，tm＋2]，［t1，t2m＋2]为插值区间。

②Lagrange插值和Neville插值起始节点和终止节点的确定：m阶插值需要m＋1个插值节点t1，t2，…，tm＋1，所 对 应 的 坐 标 值 为 X1，X2，…，Xm＋1，设 ｛Xi｝单调递增（i＝1，…，m，m＋1）.

当m＝2n＋1时，［t＿start，t＿end]＝［tn＋1，tn＋2]，n＝1，2，…，插值区间为［t1，tm].

当m＝2n时，［t＿start，t＿end]＝［tn，tn＋1]，n＝1，2，…，插值区间为［t1，tm].

2）选取插值区间节点［t1，t2m＋2]或［t1，tm]处的坐标值为［X1，X2m＋2]或［X1，Xm].

3）采用移动区间的方法进行精密星历的插值计算。

① Trigonometric插值：插值区间为［t1，t2m＋2]，用 Trigonometric插值求出［tm＋1.tm＋2]内各节点所对应的坐标值。

②Lagrange插值、Neville插值：当m＝2n＋1时，插值区间为［t1，tm]，可用 Lagrange插值或Neville插值求出［tn＋1，tn＋2]内各节点所对应的坐标值；当 m＝2n 时，插值区间［t1，tm]，可 用Lagrange插值或 Neville插值求出［tn，tn＋1]内各节点所对应的坐标值。

4 实验结果与分析

以30min间隔的卫星位置插值15min间隔的卫星位置。采用2011年1月29日PRN2的15 min间隔的精密星历，精密星历数据是由以下分析中心提供的：IGS、NGS、ESA、NRCan、ESA、JPL、MIT、SIO。利用相关程序提取各分析中心30min间隔的卫星位置作为已知的插值节点，将各分析中心的卫星位置求平均值作为15min间隔的卫星位置的真值，采用基于移动区间的插值方法进行插值计算，比较出各分析中心的数据质量，采用数据质量比较好的分析中心提供的数据进行插值计算，分析随着插值阶数的增加，插值方法的变化，插值精度的变化情况。

4.1 不同数据产品的数据质量比较

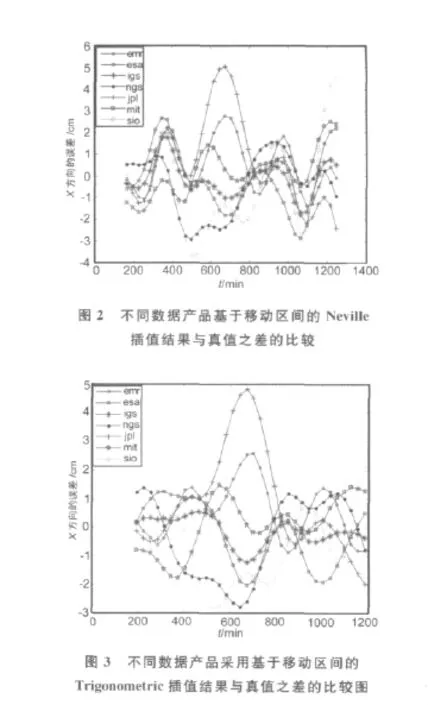
分别将7家分析中心2011年1月29日PRN2的30min间隔的数据采用基于移动区间的Lagrange多项式插值、Neville多项式插值、Trigonometric多项式插值方法进行插值计算，插值到11阶。将插值结果与各分析中心的平均值即真值之间进行求差，得到的结果如下图所示。

图1、图2和图3中各分析中心的插值结果与真值的坐标差是基于移动区间的Lagrange多项式、Neville多项式、Trigonometric多项式在11阶时与真值的坐标差。在图1、图2、图3中画两条额外的深虚线，分析各图可知：由IGS提供的精密星历数据经过内插之后与真值之差全部在±2cm之内，而其他分析中心的数据产品的插值结果与真值之差有部分数据落在虚线外。因此，IGS分析中心提供的精密星历质量比较好，在将来的计算中，需要特定时间间隔的卫星位置时，首选IGS提供的精密星历数据进行插值计算。

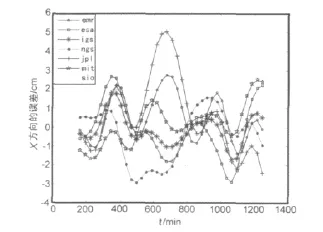
图1 不同数据产品基于移动区间的Lagrange插值结果与真值之差的比较图

4.2 各插值方法精度比较

经过上面的实验分析，IGS分析中心提供的精密星历数据质量比较好。将IGS提供的2011年1月29日PRN2的30min间隔的精密星历分别采用基于移动区间的Lagrange插值、Neville插值、Trigonometric插值内插到15min，并与IGS提供的15min间隔的数据（称为真值）进行比较。计算结果如表1所示。

进行分析可知：

1）Lagrange插值方法和Neville插值方法的插值精度相同。

2）采用基于移动区间的插值方法收敛比较迅速，并且随着阶数的增加，插值精度比较稳定，在特定的阶数下Neville多项式插值和Trigonometric多项式插值方法均能达到亚厘米级的精度。

3）基于移动区间的Neville多项式插值在11阶时可以满足精度要求，并且在11阶以后收敛，可以达到亚厘米级的精度，而Trigonometric收敛速度更快，在4阶时就能满足精度要求，并且在4阶以后收敛，同样，也能达到亚厘米级的精度要求且精度保持稳定。

4）基于移动区间的Neville插值方法的收敛速度较Trigonometric插值方法慢，而Trigonometric插值方法理论知识比Neville插值方法复杂，但是Trigonometric插值方法考虑了卫星坐标分量的周期性，本身精度就很高，加上移动区间的方法，使其精度更加稳定，因此，Trigonometric多项式插值方法是实现卫星位置内插计算的一种行之有效的方法。

对表1为了进一步比较三种方法的插值精度，将多项式插值到12阶的结果与真值之间求差，由于Lagrange与Neville插值精度相同，本文只比较Neville与Trigonometric的插值精度。结果如图4所示。

表1 基于移动区间的Lagrange插值、Neville插值和Trigonometric插值结果

图4 两种插值方法结果比较

图4为Neville多项式、Trigonometric多项式插值到12阶时与真值之差。分析图4可知：

1）对于Neville插值方法X和Y方向的误差在±1cm，Z方向的误差在±5cm之内，对于Trigonometric插值方法，X和Y方向的误差在±5mm，Z方向的误差在±2mm之内。因此，基于移动区间的Trigonometric多项式插值精度比基于移动区间的Neville多项式插值精度高。

2）图中画出的是两种插值方法插值到12阶时的情形，结合表1可以得出，当插值阶数上升到一定的程度，两种插值方法的精度相差不大。但就收敛速度而言，基于移动区间的Trigonometric多项式插值方法的收敛速度比其他两种插值方法都要快，并且插值精度整体上优于Neville多项式插值和Lagrange多项式插值的插值精度。

5 结 论

1）在精密星历内插的过程中，单独使用Lagrange、Neville、Trigonometric等插值方法，随着阶数的增加，插值精度会发生衰减或不稳定的现象，本文提出的基于移动区间的插值方法有效的解决了这一问题，插值精度较高且插值结果稳定。

2）利用提出的基于移动区间的插值方法对7家分析中心的数据进行插值计算，IGS提供的精密星历数据质量比较好。

3）用IGS提供的30min间隔的数据进行插值15min间隔的数据采用基于移动区间的12阶的Lagrange插值、12阶Neville插值或基于移动区间的6阶Trigonometric插值，这些方法都可以达到亚厘米级的精度，满足精密定位的要求。在今后的应用中，15min插值5min、5min插值30s等均可采用本文提出的移动区间方法进行精密星历的插值计算。

［1]FENG Yan－ming，ZHENG Yi.Efficient interpolations to GPS orbits for precise wide area applications［J].GPS Solutions，2005（9）：273－282.

［2]张守建，李建成，邢乐林，等.两种IGS精密星历插值方法的比较分析［J].大地测量与地球动力学，2007，27（2）：80－83.

［3]彭泽泉.GPS精密星历拟合方法的研究［J].测绘科学，2010，35（supp1）：63－65.

［4]常 亮，何秀凤.基于移动区间的GPS轨道标准化方法［J].大地测量与地球动力学，2009，29（1）：110－113.

［5]SCHENEWERK M.A brief review of basic GPS orbit interpolation strategies［J].GPS Solutions，2003（6）：265－267.

［6]洪 樱，欧吉坤，彭碧波.GPS卫星精密星历和钟差三种内插方法的比较［J].武汉大学学报·信息科学版，2006，31（6）：516－518.

［7]李庆杨，王能超，易大义.数值分析［M].北京：清华大学出版社，2001.

［8]邓建中，刘之行.计算方法［M].西安：西安交通大学出版社，2001.

［9]邱 蕾，廖远琴，花向红.基于IGS精密星历的卫星坐标插值［J].测绘工程，2008，17（4）：15－18.

［10]唐华林，邓翠美，匡翠林.一种基于三角函数多项式的GPS轨道标准化方法［J].测绘与空间地理信息，2007，30（4）：85－88.

［11]HU Hui，FANG Lian.Interpolation and fitting algorithms for GPS satellite orbit［C]∥Proceeding of SPIE，2009.