径向磁力轴承结构设计软件系统的开发

朱晓明

（哈尔滨工程大学 工程训练中心，黑龙江 哈尔滨 150001）

磁力轴承是一种利用电磁力将转子悬浮于空间实现非接触式支撑的装置，具有无摩擦、无需润滑、无油污染、能耗低、噪声小、寿命长等优点，特别适用于真空、超静、高速等特殊环境中，在工业领域得到日益广泛地应用。随着磁悬浮技术的日益成熟，磁力轴承商品化、系列化成为必然趋势。结构设计作为电磁计算、控制系统设计和相关分析的基础，更有必要对磁力轴承的结构设计进行深入研究。在这种情况下，开发出一个结构设计软件系统，是降低磁力轴承设计成本和缩短产品开发周期的有效途径。

目前磁力轴承的设计有3种方法：

第1种方法是以约束条件和目标函数进行磁力轴承的设计，其中约束条件是系统的承载力不能低于最大承载力，另一个约束条件是线圈在产生最大承载力时需要的最大磁感应强度不能超过铁芯的饱和磁感应强度，而目标函数是磁轴承的体积最小。但是此种方法给出的计算方法如果缺乏足够的计算条件，会很难求出具体的结构参数。

第2种方法是通过最大承载力为已知条件，通过理论公式进行逆推，求取各个参数，比如磁极面积，线匝数等一些系统参数，并通过预先设定一些可变参数，比如偏置电流，来求得结构参数，比如磁轴承的内外径，磁极高度和宽度。但是该种方法所设计的结构只在主体结构上满足要求，无法在细节上满足实际磁轴承的设计。

第3种以理论和经验公式结合，进行结构设计，能够满足结构要求和性能要求。

笔者以第3种方法为基础，结合哈尔滨工程大学自由探索计划的飞轮储能项目，以径向磁力轴承的结构设计为软件设计目标，从结构、电气角度来完成参数化的软件设计。

1 径向磁力轴承结构设计

定子线圈槽的形状主要有圆形槽、梯形槽和矩形槽3种，根据比较，本软件以圆形槽为基础进行设计。同时，为了降低磁极间的耦合效应，符合经济性要求，磁极数选为8极。

磁力轴承定子转子结构示意图如图1所示。转子的初始外径d根据设计取50 mm，轴承的单边气隙大小为s，根据实际情况来选择，其值一般取s=0.2～0.5 mm，目前初始值取0.3 mm。

径向轴承的定子的内径D2=d+2s=50+2×0.3=50 mm

当径向轴承中的磁感应强度B=Bmax（最大磁感应强度）时，产生最大电磁吸力为

图1 磁力轴承定子转子结构示意图Fig.1 Structure diangram of magnetic bearing stator and rotor

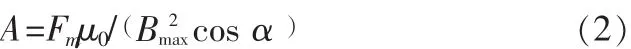
初步估算：Bmax=1.5 T （根据具体硅钢型号查，Bmax=0.9 Bsat），μ0=4×π×10-7（磁场常数），α=22.5°（一对磁极间夹角的一半），Fmax=200 N（由转子的结构计算得出）。 可得：A=（200×4×π×10-7）/（1.5×1.5×cos（π/8））×106=120.90 mm2

单极极柱面积：

定子的极靴弧长：

其中 e 为两个磁极间距离，且一般取 e=（10～20）×s。

初步估算：e=20×0.3=6 mm，系数暂取20倍。

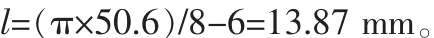
定子的磁极宽度：

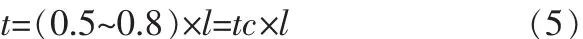
其中tc为磁极宽度和极靴弧长间的系数。

初步估算：t=0.6×13.87=8.32 mm，系数暂取值0.6。

定子磁轭宽度：

其中h、h0为磁极高度，且可以近似取值

初步估算：取 h0=0.2×h，系数暂取 0.2。

在设计磁力轴承时希望当线圈中的电流为最大值时，在磁路中能够激励其最大磁通密度，有：

在线匝数nImax中，n为一对磁极上的线圈匝数。己知线圈槽中导线直径dw，线圈填充系数λ=0.5～0.7，所以线圈槽的面积用导线的面积和表示为：

则导线的横截面积（dw对应的截面积）与所能通最大电流Imax的关系为：

转子磁扼宽度c′应与径向定子的磁极宽度t相同，即有：

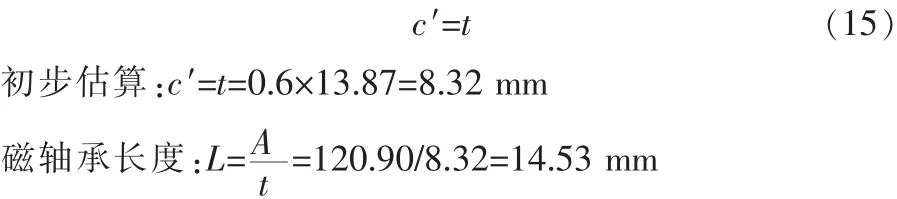
2 主要电参数设计

在求定子的电参数时，选择Imax为控制系统的主要约束，可以求得最大线圈匝数：

初步估算：取Imax=3A（根据实际情况选择功率放大器能够保证的最大电流 Imax）。 则有：n=（2×1.5×0.3×0.001）/（4×π10-7×3）=239匝。由此可以确定导线的直径：

偏置电流设计：

3 磁力轴承设计系统的软件设计

以上推导的径向磁力轴承理论和经验公式，是磁力轴承结构设计的基本过程。但是在具体计算时，由于各个因素参数之间相互约束和相互关联，一般不可能通过一次计算完成预期的目标，需要反复进行多次计算，衡量各个因素之间的制约关系，最后选择适合的参数，综合各发面因素才能最终达到满意效果。

软件设计主要采用参数化的程序设计方法，根据不同的参数变化来进行不同类型结构的磁力轴承的结构设计。考虑到轴承的系列化以及多次计算的过程，在进行参数设置时，既要考虑与当前应用相关的一些特定参数，也要考虑一些取值范围可变的经验参数以及一些适合所有应用的固定参数，最后才能生成结果数据。

根据以上分析，将设计软件的交互数据分为4类：1）固定参数，比如磁场常数，适合所有应用，因此不需要在人机界面中显示；2）应用相关的特定参数：比如最大电磁力、转子外径、单边气隙等，这些参数是设计一个轴承的重要前提条件，需要在人机界面中显示，并可改动；3）经验参数，比如各种结构之间的比例系数，电流和导线截面积的系数等，这些参数需要根据具体情况和结构条件，灵活选取，因此需要在人机界面中显示，并可改动，并需限制其范围；4）结果数据，根据上述的公式所生产的各种结构参数和电气参数。

为了实现设计系统的交互功能和参数化的实时更新，采用了Microsoft Visual C++6.0的可视化程序设计软件。在进行人机界面设计时，根据上述的分析，将人机界面设计为3个模块：特定参数模块、经验参数模块和结果参数模块。根据上述方法设计的径向磁力轴承结构设计软件的人机界面如图2所示。

在界面中，用户需要首先确定特定参数模块中的参数：磁极个数、最大磁感应强度、静态磁感应强度、饱和磁感应强度、最大电磁力、转子外径、单边气隙以及线圈填充系数等几个重要参数，然后再选择经验参数模块中的一些经验系数，通过点击“参数更新”按钮，即可完成该轴承的结构设计计算，并在结果数据模块中实时显示该条件下各结构参数和电参数的设计结果，方便准确，大大减少了设计人员的计算量。通过多组数据的对比，可选择其值的最优方案。

图2 径向磁力轴承结构设计软件的人机界面Fig.2 Interface of structure design software for radial magnetic bearing

4 结 论

磁力轴承的结构设计是关系到其支撑性能稳定性和可靠性的重要基础，也是进行支撑系统设计的重要一环。它的设计过程需要经过多次计算，平衡多个参数之间的制约关系，达到整体的一个均衡效果。

为了避免多次计算的复杂过程，并进行后续型号的系列化，利用计算机编程技术，把磁力轴承结构的常规结构设计和电参数设计转化为实际可用的软件工具，通过参数化的程序设计方法和人机交互模式，能够较好的简化结构设计工作，将大大缩短磁力轴承结构的设计周期、提高设计效率、保证设计参数结果的最优化，从而保证磁力轴承结构的正确性和可靠性。

[1]陈湘舜，曾虎彪.飞轮储能用磁力轴承的发展研究[J].机床与液压，2011，38（8）：128-132.

CHEN Xiang-shun，ZENG Hu-biao.Development research of magnetic bearing technology for flywheel energy storage system[J].Machine Tool&Hydraulics， 2011，38 （8）：128-132.

[2]陈龙.磁力轴承结构参数化设计[D].武汉：武汉理工大学，2005.

[3]张钢，殷庆振，蒋德得，等.磁悬浮轴承-柔性转子系统的结构设计[J].轴承，2010（6）：15-18.

ZHANG Gang， YIN Qing-zhen， JIANG De-de， et al.Design of flexible rotor system supported by AMB[J].Bearing，2010（6）：15-18.

[4]万金贵，汪希平，李文鹏，等.径向磁力轴承的结构分析与优化设计方法[J].武汉理工大学学报，2010，32（1）：62-65.

WAN Jin-gui， WANG Xi-ping， LIWen-peng， etal.Structure analysis and optimized designmethod for radial magnetic bearing[J].Journalof Wuhan University of Technology， 2010，32（1）：62-65.

[5]赵韩，王勇.径向电磁轴承结构设计与分析[J].农业机械学报，2005，36（7）：122-125.

ZHAO Han，WANG Yong.Design and analysis of radial active magnetic bearings[J].Transactions of the Chinese Society for Agricultural Machinery， 2005，36（7）：122-125.

[6]张海波，杨昌茂，段建华.径向永磁偏置磁悬浮轴承转子模态分析[J].机械制造，2011，49（3）：26-28.

ZHANG Hai-bo， YANG Chang-mao， DUAN Jian-hua.Modal analysis of radial permanent magnet offset magnetic levitation bearing rotor[J].Machinery， 2011，49（3）：26-28.