预测反馈补偿法抑制帧中继网络时延抖动

周启荣，周阳辉

（中国卫星海上测控部 江苏 江阴 214431）

卫星通信帧中继网络承担着远洋测量船航渡期间的通信保障任务，在数据链路层采用帧中继协议传输话音、视频和数据等信息。时延抖动是QoS的重要指标[1]，当其超出一定范围时，数据帧会因为迟到太久而被丢弃，导致语音、视频等多媒体业务受到严重影响，因此研究抑制时延抖动的方法是很有意义的。抑制时延抖动主要有两个切入点，一是优化调整卫星通信系统参数设置，提高网络传输性能，从根本上减少产生时延抖动的因素；二是通过辅助处理方法抑制已经产生的时延抖动，常用的办法有缓冲区设置法[2-3]，它让所有的帧数据都在缓冲区等待，使得所有帧数据经历的时延都变成了一个最大的时延；另一种则是针对复杂拓扑结构网络的路由约束算法[4-5]，它用最短路径算法来获得最小时延路径，并在此基础上建立时延抖动约束条件，从而建立解Steiner树问题，寻找出满足时延抖动约束条件的路由路径。卫星通信帧中继网络具有平均时延大、结构简单的特点，因此不适合采用上述两种方法，本文在详细分析卫星通信帧中继网络时延抖动产生原因的基础上，建立时延抖动的数据模型，并提出预测反馈补偿算法抑制产生的时延抖动。

1 帧中继网络时延抖动

1.1 产生原因

简化的卫星通信帧中继网络帧数据传输经过的环节如图1所示，其中产生时延和时延抖动的原因主要有以下几点：

1）编码时延产生在设备侧，如果设备的编码方式固定，则编码时延也固定，产生的时延抖动也较小，可以忽略。

2）传输时延表示为（1），其中，L为发送的帧数据长度，R链路传输速率。如果采用固定长度帧时，那么传输时延是固定的，那么产生的时延抖动可以忽略。

3）排队时延表示为（2），其中N为缓冲区内排队帧个数，Li为第i个帧长度，R为链路传输速率。当一个帧数据进入发送队列缓冲区排队时，排队长度N和帧长度Li都是不可预知的，它们都是随机变量，造成的排队时延也是一个随机变量，它们也是产生时延抖动的主要因素。

图1 卫星通信帧中继网络中帧传输示意图Fig.1 Sketch map of transmitting framers in satcom frame relay network

4）传播时延表示为（3），其中，H为地球同步轨道卫星距地面高度，c为电磁波在空间的传播速度，由于卫星高度H相对固定，因此传播时延dp也相对固定，产生的时延抖动也可以忽略。

根据上述分析可知，编码时延和传播时延相对固定，产生的时延抖动可以忽略；而帧数据长度和排队长度的随机性则导致不同帧数据经历的时延产生变化，从而产生时延抖动。

1.2 数据模型

以卫星通信帧中继网络中DLCI表示的虚电路为例，假设发送端发送每一帧的绝对时间为 x（n），n=1，…，N，N，为需要发送的帧个数，接收端接收每一帧的绝对时间为y（n），每一帧经历过的时延定义为d（n）：

时延抖动则定义为前后两帧经历时延的变化，表示为：

在实际计算时，发送端和接收端的绝对时间是有误差的，为了抵消这一误差，将时延抖动的表达式进行改写，结合上述两式可以得到：

其中 Δy（n）=y（n）-y（n-1）、Δx（n）=x（n）-x（n-1），即时延抖动 J（n）表示接收端接收每一帧间隔 Δy（n）与发送端发送每一帧间隔Δx（n）之差，而发送帧和接收帧的时间间隔可以在两端准确地获得，如图2所示。

图2 发送端和接收端发送时间间隔Fig.2 Interval time between sender and receiver

根据卫星通信帧中继网络时延产生的原因，我们可以将每一帧经过的时延看作是一个随机过程，产生的时延抖动也是一个随机过程，同理 Δy（n）、Δx（n）也都是随机过程[6]。 不失一般性，在此假设这三个随机过程是广义平稳的，因为满足式（6），所以它们之间具有一定的相关性。

依据式（6），为了使时延抖动 J（n）等于零，可以得到：

它的物理意义是：根据接收端的时间间隔 Δy（n），可以通过调整发送端统计复用发送帧的时间间隔Δx（n），使得时延抖动J（n）为零，本文正是基于此时延抖动数据模型，提出预测反馈补偿的方法来抑制时延抖动。

2 预测反馈补偿模型

预测反馈补偿模型由两个部分组成，一是自回归（AR）预测模型。接收端根据接收到的帧数据，计算每一帧的到达时间间隔，并根据这些观测值采用AR模型预测下一帧的到达时间间隔；二是反馈补偿回路。接收端在预测出下一帧到达的时间间隔后，通过反馈回路送给发送端，并利用该值补偿调整发送端发送下一帧的时间间隔，从而达到抑制时延抖动的目的。

2.1 AR预测模型

AR模型是平稳随机过程的一种标准线性模型，表示均值为零、方差为σ2e的白噪声通过全极型滤波器（FIR）获得的随机信号序列，反之，当信号序列满足AR模型时，通过该模型可以“准确”地预测序列的下一个值，使得预测后误差的均方值达到最小。

已知有一个观测序列 Δy（n），n=1…N-1，它的 p阶 AR 预测模型为：

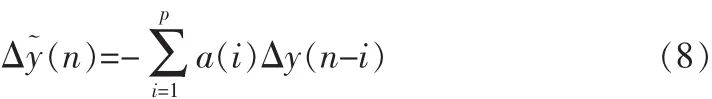
即在获得模型参数a（i）后，可以利用最近的p个观测值计算下一个值。本文采用Burg算法[8]求解模型参数a（i），在计算过程中只利用观测数据，通过Levinson递归关系进行迭代计算，算法的具体过程如下：

1）初始化前向预测误差、后向预测误差、平均预测误差功率，计算一阶模型p=1：

4）更新滤波器输出的前向预测误差和后向预测误差：

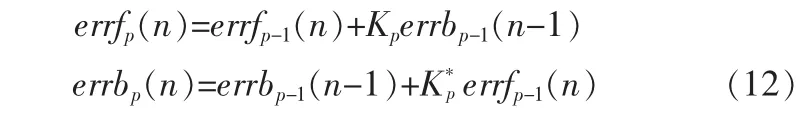
5）更新平均预测误差功率：

6）判断预测误差功率，当 ρ（p）大于门限 σ2λ时，p+1→p，重复 2）→6）；当 ρ（p）小于门限 σ2λ时，跳出迭代，输出模型参数：预测阶数 p，预测系数 ap（i），i=1，…，p。

7）依据预测公式（8），计算观测序列的第N个值：

可以证明[8]，对于一个符合有限阶次AR过程的观测数据，Burg算法能够得到精确的AR模型参数。但是信号往往不能够完全满足AR模型，同时也不会是有限阶次的，预测误差肯定大于σ2e，增加预测阶次p可以使预测误差尽可能接近σ2e。

2.2 抑制时延抖动

根据时延抖动的数据模型，为了让时延抖动J（n）为零，需要调整发送端的时间间隔，使得接收端的时间间隔与发送端的时间间隔相等，再结合AR预测模型，预测反馈补偿算法抑制时延抖动过程如下：

1）接收端根据接收到的帧，计算帧到达的时间间隔Δy（n）；

图3 预测补偿模型示意图Fig.3 Sketch map of prediction and compensation model

当接收端下一帧到达之后，计算出真实的时间间隔Δy（n+1），如果预测准确，则：

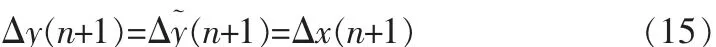
即下一帧的时延抖动为零。但是随机变量的预测不能是精确的，必然存在预测误差，记为：

即接收端时间间隔预测误差ey（n+1）等于处理之后的剩余时延抖动 ΔJ（n+1）。

为了获得满足要求的时延抖动值，就要求AR模型预测之后的预测误差满足要求。根据QoS要求，时延抖动超过允许的最大值Jm的概率小于ε，可以表示为：

在进行处理之前，由于时延抖动大，不能满足式（18）的条件，抑制时延抖动的处理过程也就是满足该条件的过程，假设卫通链路时延抖动J（n）满足正态分布（服从其他的分布类型时，处理的方法一致），均值为零，方差为σ2J，则根据正态分布函数[7]可以计算出满足式（18）要求的方差为：

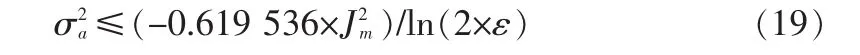
又根据式（17），剩余时延抖动等于接收端时间间隔的预测误差，在利用AR模型预测时，令预测误差门限值σ2λ满足：

满足目标式（18）的要求，可以看出，抑制时延抖动的过程就是修正时延抖动的概率分布的过程，即改变正态分布函数的方差。

3 仿真实验

根据卫星通信帧中继网络的系统参数设置和QoS要求，本文通过MATLAB仿真实验来证明所提算法抑制时延抖动的有效性。

3.1 参数设置

远洋测量船卫星通信帧中继网络帧数据经历的时延有编码时延、传输时延、排队时延和传播时延。在固定帧长度条件下，时延主要为传播时延，大约为270 ms，时延抖动则主要由排队时延造成，其他则忽略不计。

因此仿真时假设帧数据经历的平均时延为270 ms，卫通链路的时延抖动满足正态分布，均值为0，方差为σ2J=400 ms2，在传输语音和视频信号时，当时延大于300 ms，或者丢包率大于0.3%时人的感官将无法忍受，因此能容忍的最大时延抖动为Jm=30 ms，缓冲区将大于最大时延抖动的帧数据全部丢弃，根据式（19）可以计算出能够容忍的时延抖动的方差为：MATLAB仿真关键过程如下：

1）生成一组时延抖动量，满足正态分布，均值为0，方差为 σ2J=400 ms2。

2）计算接收端帧到达的实际时间间隔序列Δy（n）。

3）通过AR预测模型计算下一帧到达的时间间隔Δy˜（n+1），在预测过程中，令σ2λ≤σ2a。

3.2 仿真结果

根据上述仿真流程，最后得到剩余时延抖动的方差为σ2ΔJ=101 ms2，满足概率分布的要求，图4表示的是处理前后时延抖动值，可以看出处理前的时延抖动值变化范围大，最大时延抖动超过80 ms，处理后的时延抖动则被约束在更小的范围内，最大时延抖动满足指标要求，小于30 ms。

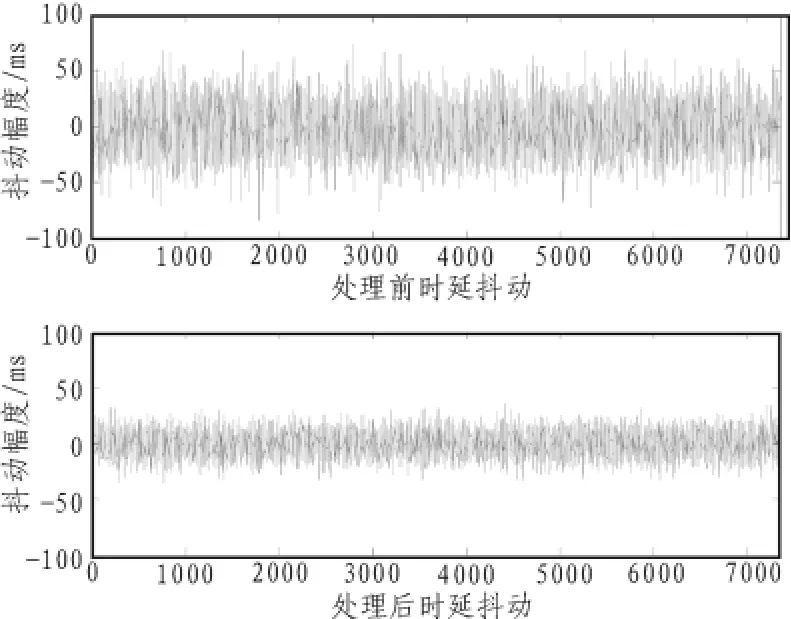
图4 预测补偿前后时延抖动值Fig.4 Delay jitter values before and after prediction and compensation

另外，将预测过程中的预测门限值σ2λ设置成一个比较小的固定值，比如50 ms2，然后更改AR模型的预测阶次p，获得的实验结果如表1所示。

表1 预测阶次与剩余时延抖动方差的关系Tab.1 The relationship of prediction ranks and variance of residual delay jitter

从表中可以看出，预测阶次p越高，AR模型预测更加准确，预测误差更小，获得的剩余时延抖动的方差越小，从正态概率分布来看，时延抖动值被约束在更小的范围，即预测补偿模型可以有效地降低接收端和发送端之间的时延抖动。

4 结束语

卫星通信帧中继网络由于数据帧的长度和缓冲区排队长度的随机性，导致产生时延抖动，本文用接收端和发送端的帧数据时间间隔差来表示时延抖动，利用AR模型对接收端的时间间隔进行预测，并据此调整发送端的时间间隔，补偿处理抵消时延抖动的影响。最后应用MATLAB软件进行仿真实验，结果验证了所提模型算法的有效性，时延抖动范围大幅度下降，可以满足QoS要求。

[1]陈启美，李嘉编著.现代数据通信教程[M].南京：南京大学出版社，2002.

[2]Verma D C，ZHANG H，Ferrari D.Delay jitter control for real-ime communication in a packet switching network[J].IEEE Conference on Communications for Distributed Applications and Systems，1991：35-43.

[3]周康，裘楷，吴宇红.VoIP系统中消除时延抖动的研究与实现[J].电子科技，2007，（1）：51-54.

ZHOU Kang，QIU Kai，WU Yu-hong.Research on and implementation of jitter elimination in the VoIP system[J].Electronic Sci.&Tech，2007（1）：51-54.

[4]王明中，谢剑英，张敬辕.时延及时延抖动限制的最小代价多播路由策略[J].计算机学报，2002，25（5）：534-541.

WANG Ming-zhong，XIE Jian-ying，ZHANG Jing-yuan.Strategy of constructing minimum cost multicast routing tree with delay and delay variation Bounds[J].Chinese J.Computers，2002，25（5）：534-541.

[5]余燕平，仇佩亮.时延和时延抖动约束的低费用多播路由算法[J].电路与系统学报，2001，6（4）：65-68.

YU Yan-ping，CHOU Pei-liang.A low cost multicast routing algorithm with delayand delay variation constraints[J].Journal of Circuits and Systems，2001，6（4）：65-68.

[6]Fulton A C，LI San-qi.Delay jitter first-order and secondorder statistical functions of general traffic on high-speed multimedia networks[J].IEEE/ACM transactions on networking，1998，6（2）：150-163.

[7]La C A， Lombardo A， Palazzo S，et al.QoS requirement control in delay jitter sensitive multimedia Services[J].IEEE Conference on Gateway to Globalization，1995：1243-1247.

[8]皇甫堪，陈建文，楼生强.现代数字信号处理[M].北京：电子工业出版社，2003.