网络端端可靠度的上下界计算研究

乔晓东，毛 志，邓宏钟

（国防科技大学 信息系统与管理学院，湖南 长沙 410073）

21 世纪以来，随着信息技术的飞速发展，人类社会加快了网络化进程。从Internet到www，从交通网络到通信网络，从电力网络到物流网络……可以说，我们被网络包围，几乎所有的复杂系统都可以抽象成网络模型，网络已成为人们生产、生活中不可缺少的一部分。

随着网络技术的不断发展与应用，对网络的定量与定性特征的科学理解，已成为网络时代科学研究中一个极其重要的挑战性课题，甚至被称为“网络的新科学”[1]。其中网络可靠性是对网络定量理解的一个非常重要的参数[2]，网络的可靠性也是保证系统正常运行的前提，因此很多先驱都投身研究网络的可靠性问题。网络就是有一些带有连边的节点组成。在网络可靠性的研究中，人们常常用概率图来表示网络，图的点和边都分配给正常运行的概率。早期对网络可靠性的算法研究主要为精确计算，算法包括状态枚举法、容斥原理法、不交积和法、因子分解法、随机过程法等等，这些精确算法随着网络单元数量和复杂程度的增加，计算难度成指数增长。以状态枚举法为例，对于一个不考虑节点失效的含有M条边的无向网络来说，共有2M个状态向量，计算量相当大，即使是计算机也难以在有意义的时间内完成计算，目前网络可靠度的精确算法只适用于规模较小的网络。可靠性度量参数的精确计算被Ball[3]等人证明为NP-hard问题后，研究人员开始了对近似算法的研究。近似算法主要包括定界法、蒙特卡洛法和图形变换法[4]。所提出的这些近似算法大部分都是启发式算法，而且无法预测计算结果的误差大小，只有定界法避免了这个问题。定界法的主要思想就是通过数学的方法改变可靠性精确计算的代数结构，从而得到可靠性的边界值。1972年Van Slyke和Frank[5]第一个用多项式计算网络可靠性的上下界，1982年Ball和Provan[6]对算法进行了改进。研究者根据不同的思路提出了大量的算法来计算网络可靠性的界，研究得比较好的界有Colboum界[7]（1988年）、Ball-Provan界[8]（2006年），2004年冯海林给出了基于网络连通子网数与网络割集以及断集数的全端可靠性上下界评估法[9]，2006年Satitsatian和Kapur[10]通过寻找下界点的方法来计算多态网络端端可靠性的下界。其中利用多项式计算网络全端可靠性的关键是多项式中系数的计算，而且大部分系数的精确计算都比较困难[9]。

本文利用节点遍历法求解网络端端最小路，避开精确计算的不交化的复杂性，基于最小路集计算端端可靠度上界。引入端端不交最短路集的概念，来分析复杂网络的可靠度，计算网络端端可靠度的下界。两个边界算法简单便捷，便于编程实现。最后结合实例，将计算结果与端端可靠度精确值进行比较分析，阐述本算法的有效性，并说明该算法的适用性。

1 问题描述与基本假设

1.1 基本定义

所谓一个网络，它是由一些节点以及连接这些节点的边组成。从数学的观点看，网络就是一个图（但复杂网络又与图有本质区别）。为此我们给出图的定义。

定义 1 称数学结构 G={V（G），E（G），φG}[11]为一个图，其中 V（G）是非空集合，φG是从集合 E（G）到 V（G）×V（G）的一个映射，则称G是一个以V（G）为顶点集合，以E（G）为边集合的（有向）图。

图中的节点是不带圈的，即不存在从该节点流出又流入该节点的边；图中的边不重复出现，即不存在同一条边连接两个以上的节点。

定义2 从指定节点s，经过一串边序列可以到达节点t，则称这个边序列是从s到t的一条路。

定义3 从节点s到节点t的边序列称作一条最小路，若满足：1）它是一条路；2）最小性，即从这个边序列中除去任意一条边后它将不再是从s到t的路。

定义4 没有公共边的端端最短路集称为不交最短路集。

1.2 问题及基本假设

本文研究的问题是端端可靠性问题，也就是求解网络源点s可以到达终点t的概率，本文重点对该概率的上下界进行计算。在定量计算网络端端的可靠度时，还需做以下假设：

1）边或系统只有两种状态：正常或者故障状态；

2）节点的可靠度为1，即不考虑节点的故障；

3）每条边之间的故障是相互独立的，即任意一条边的故障不会引起其他边的故障。

2 基于最小路集的端端可靠度上界算法

上界算法的基本思路是利用节点遍历法求出网络端端的所有最小路集后，直接将所得到的最小路集做为端端的并联单元，而每条最小路认为是所含各边的一个串联模型，这样构成一个串并联系统，利用这个模型计算网络端端可靠度。由于计算过程中并没有去除端端最小路集之间的冗余，也没有对最小路集进行不交化处理，所以计算结果总大于精确值。

2.1 算法参数与符号说明

G—网络的邻接矩阵；

s—网络源节点；

t—网络汇节点；

E（i）—离开节点i的链路数，即从节点i出发，下一步可到达的节点数；

R（j，M）—路线矩阵，第j行各列元素表示从节点j出发，下一步可到达的节点的标号；

C（ j）—数组 R 第 j行元素的列号，R（ j，C（ j））记录 j下一步到达的节点标号；

Path（v，m）—第m条路的节点序列中的第v个节点；

Um—第m条路中的节点数目；

F（K）—检验节点在前面是否走过以及是否到达输出节点而设置的开关标志。

2.2 网络端端可靠性上界算法

输入：网络图的邻接矩阵 G，源点 s，终点 t，网络各边的可靠度p；

输出：网络端端s-t可靠度的上界值Ru

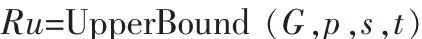
Step 1初始化。

由网络的邻接矩阵计算得出路线矩阵R以及向量E，并对参数赋初值：n=length（G）；C=[C（1），…C（n）]，C（i）=1，i=1，…n；j=1，Path（1，1）=s，m=1，v=2；

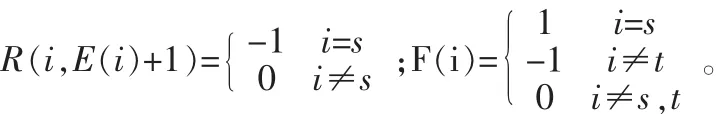
其中Pathnum表示最小路集的条数，Rn表示第n条端端最小路的可靠度。

3 基于不交最短路集的端端可靠度下界算法

下界算法的基本思路是通过逐次删除最短路的方法来求解网络端端的所有不交最短路，直到网络端端不连通为止。该算法求得的各条最短路不含有公共边，故可以直接使用串并联模型对其进行计算。由于算法在求解各不交最短路集的过程中，因为删边而减少了网络端端路径的数量，所以计算端端可靠度的值要小于精确值。

确定端端可靠性下界的算法如下：

输入：网络图的邻接矩阵 G，源点 s，终点 t，网络各边的可靠度p；

其中m表示不交最短路的条数，Rn表示第n条端端最短路的可靠度。

4 示例应用及分析

为了说明本算法，下面我们给出算例。

4.1 网络边的可靠性概率值恒定

图1是由随机网络模型生成的含有5个节点、8条边的随机网络。考虑图1所示网络系统从节点1到节点5的可靠度的问题，利用本文算法计算网络端端1-5的可靠度上下界并与由BDD[12]算法计算的精确值进行比较分析。不考虑网络节点的可靠性，对网络边的可靠度取p=0.01：0.01：1，比较结果如图2所示。

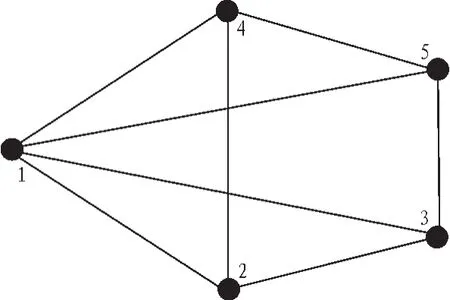
图1 ER网络Fig.1 Random graph

很显然Ru≤R≤Rd，当且仅当网络系统为特殊的串并联系统时，不等式取等号。采用本文算法对大量网络进行测试，发现网络端端可靠度的精确值在通常情况下可以表示为R=（Ru+Rd）/2，图3 为本算例节点 1～5 可靠度精确值 R 与（Ru+Rd）/2 的比较结果，本例计算显示最大误差为0.008 95，最小误差为0。

4.2 网络边的可靠性概率值变化

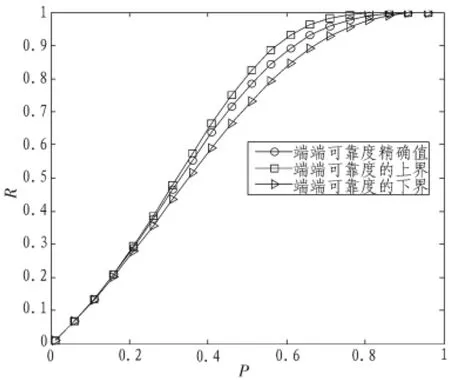
图2 精确值与上下界比较Fig.2 Comparison of exactness&&upper and lower bounds

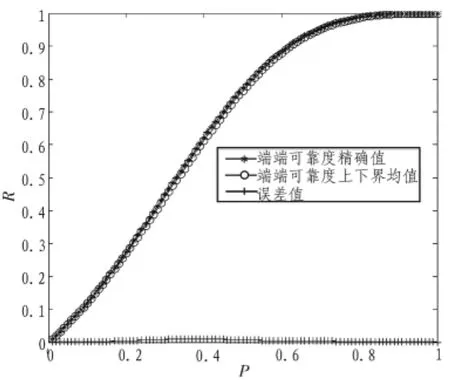
图3 精确值与上下界均值比较Fig.3 Comparison of exactness&&average of upper and lower bounds

现实中网络部件的可靠度并不是一成不变的，而是随着时间连续变化，也就是说任何元部件都有一定的寿命，且其可靠度随着时间的推移逐渐下降。本文模型可以分析网络端端可靠性随时间的变化情况。不失一般性，假设野战地域通信网的基本结构图4的边的可靠度概率服从负指数分布，Redge（i）=P（T）=λe-λT（T＞0），分析网络端端 5～7 的可靠度随时间的变化情况。

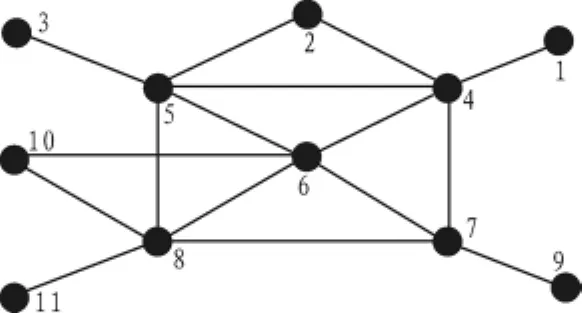
图4 基本网络结构Fig.4 Basic network framework

在λ=0.7时，网络5～7端端可靠度的上下界随时间的变化情况，如图5所示。网络端端可靠性的上下界也随时间呈现负指数变化规律。

5 结束语

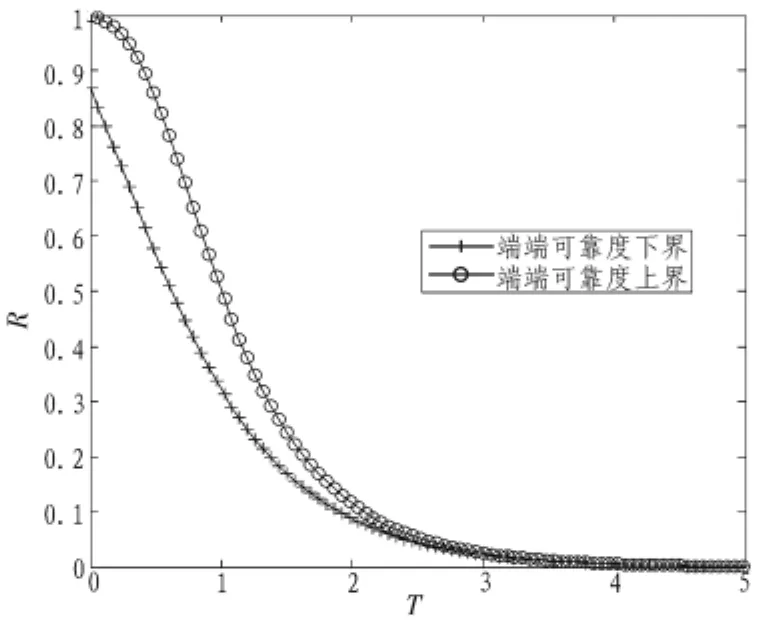
图5 网络端端可靠性随时间的变化Fig.5 Change of network terminal to terminal reliability over time

本文基于最小路集和不交最短路集对网络端端可靠性的上下界进行了计算研究，并对大量网络进行了仿真实验，发现网络端端可靠度的精确值在通常情况下可以表示为R=（Ru+Rd）/2，通过实验比较分析，得到了较好的效果，然而如何通过算法优化网络端端可靠度上下界，使得上界值减小、下界值增大，使二者充分接近网络端端可靠度的精确值以及如何基于路径并考虑网络部件容量限制以及网络流约束精确计算网络的可靠性，是下一步需要研究的工作。

[1]Duncan，Watts J.The“New”science of networks[J].Annual.Review of Sociology，2004（30）：243-270.

[2]Morgan D E，Taylor D J， Custeau G.A survey of methods for improving computer network reliability and availability[J].Computers and Mathematics with Applications，1977，11：42-50.

[3]Ball M O.Complexity of network reliability computations[J].Networks，1980，10（2）：153-165.

[4]李瑞莹，康锐.网络可靠性评价研究综述[J].可靠性工程，2008：1-6.

LI Rui-ying，Kang rui.Review on evaluation of network reliability[J].Reliability Engineering，2008，1-6.

[5]Van.Slyke R M，Frank H.Network reliability analysis I[J].Networks，1972，（1）：279-290.

[6]Ball M，Provan J.S Bounds on the reliability polynomial for shellable independence systems[J].SIAM J.Alg.Disc.Meth，1982，（3）：166-181.

[7]Brecht T B，Colbourn C J.Lower bounds on two-terminal network reliability[J].Discrete Applied Mathematics，1988，21（3）：185-198.

[8]Ball M O，Provan J S.Calculating bounds on reachability and connectedness in stochastic networks[J].Networks，2006，13（2）：253-278.

[9]冯海林.网络系统可靠性问题的研究 [D].西安：西安电子科技大学，2004.

[10]Satitsatian S，Kapur C K.An algorithm for lower reliability boundsofmultistatetwo-terminalnetworks[J].IEEE Transactions on Reliability， 2006， 55 （2）：199-206.

[11]殷剑宏，吴开亚.图论及其算法研究[M].中国科学技术大学出版社，2003.

[12]武小悦，沙基昌.网络系统可靠度的BDD算法[J].系统工程与电子技术，1999，21（7）：1-4.

WU Xiao-yue，SHA Ji-chang.A BDD algorithm for network reliability[J].Systems Engineering and Electronics，1999，21（7）：1-4.