新安江模型参数不确定性分析

戴健男,李致家,黄鹏年,黄迎春

水文系统的不确定性是水文科学研究的难点问题之一,也是水文系统复杂性的主要体现,客观的水文过程则是确定性与不确定性各种成分共同作用的结果.水文模拟和预报的不确定性越来越受到国内外水文界的重视,国际水文科学协会(IAHS)于2003年正式启动了名为“Prediction in Ungauged Basins(PUB)”的国际水文计划,大力开展无资料地区和资料缺乏地区的水文研究[1].众多的国内外学者都分析和讨论了水文模型的不确定性问题[2-7].

Beven等于1992年提出的GLUE方法代表了水文模型不确定性研究领域的最新进展.Freek等[8]将该法应用于法国Ringelbach流域的TOPMODEL模型不确定性分析.Franks等[9]在无水文资料情况地区进行模型不确定性研究,采用GLUE方法根据贝叶斯公式由新的资料对原似然值进行更新,通过比较更新前后的不确定性估计来评价新增信息的价值.

新安江模型是由河海大学赵人俊教授于1970年提出和建立的概念性降雨径流模型[10],在我国南方湿润地区具有广泛的适用性.本文以太湖东苕溪流域和淮河息县流域为例,运用GLUE方法,研究该模型参数的不确定性问题,分析模型“异参同效”现象以及洪水模拟的概率分布.

1 GLUE方法基本原理

GLUE方法有个很重要的观点:导致模型模拟结果好与差的不是模型单个参数,而是参数组合.GLUE方法首先设定模型参数的分布取值范围,利用Monte-Carlo随机采样方法获取参数值组合,放入模型中进行模拟.选定似然目标函数,计算模型模拟结果与观测值之间的似然函数值,再通过计算函数值的权重得到各参数组合的似然值.在所有的似然值中,设定一个临界值,低于这个临界值的参数组似然值被赋为零,表示这些参数组不能表征模型在研究流域的功能特征;高于该临界值则表示这些参数组能够表征模型在研究流域的功能特征.对高于临界值的所有参数组似然值重新归一化,按照似然值的大小,求出在某置信度下模型预报的不确定性范围.

2 新安江模型敏感参数

新安江模型有两大核心理论:蓄满产流和张力水蓄水容量曲线[11].关于新安江模型的原理及应用情况可以参考相关文献,这里不再赘述.

根据文献[12-13]和前期的参数敏感性分析工作,选择蒸散发折算系数K、表层土自由水蓄水容量SM、地下水出流系数KG、壤中流出流系数KI、地下水消退系数CG、壤中流消退系数CI和河网水流消退系数CS这7个较为敏感、对模型模拟结果影响较大的参数来研究其对模型模拟结果不确定性的影响.因参数的先验分布形式不易确定,采用了均匀分布来代替.敏感参数的取值范围见表1.

3 参数不确定性实例分析

3.1 流域概况

选取东苕溪和息县两个水文特征差别较大的流域进行研究.东苕溪流域位于太湖区,属于我国中亚热带向北亚热带的过渡流域,受大陆与海洋气候的影响,季风盛行,四季分明,雨量充沛,年平均降水量1553mm左右,多年平均水面蒸发量为800～900mm.丰枯年际变幅及年内时空分布不均匀,丰水年如1954年降水量达2103mm,枯水年如1978年全年降水量仅728mm.年内分配按降雨特性大致可分为梅汛、台汛和非汛期3期,汛期雨量常占全年降水量的75%左右.

息县流域位于河南省南部,居淮河上游,流域面积8826km2(扣除南湾和石山口两座大型水库面积).该流域处于北亚热带和暖温带的过渡地带,在气候上具有过渡特征.流域多年平均年降水量1145 mm,其中50%左右集中在汛期(6—9月),最大年降水量1 486.6mm,最小年降水量512.9 mm,多年平均蒸发量为1258.5mm.

3.2 参数组“异参同效性”

将Monte-Carlo随机采样得到的10万组参数代入两个流域的新安江模型中进行模拟,分别得到10万个模拟流量过程和特征值.从这10万个模拟流量过程和特征值中发现,模拟流量过程线的整体趋势是相同的,其中有些和观测流量过程线拟合得很好,有些则或高或低地偏离观测值,充分体现出水文模型的不确定性[14-15].同时,不同参数组合可以得到十分相似的模拟似然值,即所谓的“异参同效“现象,很好地印证了GLUE方法的中心观点:导致模型模拟结果好与坏的关键并不是单个参数,而在于模型的参数组合[4].由此可见,由人工率定而来的“最优”参数组是不可靠的,具有高不确定性.表 2和表3列出了东苕溪流域1983062308号洪水和息县流域2002062120号洪水高似然值区域中的5组“等效性”参数组.

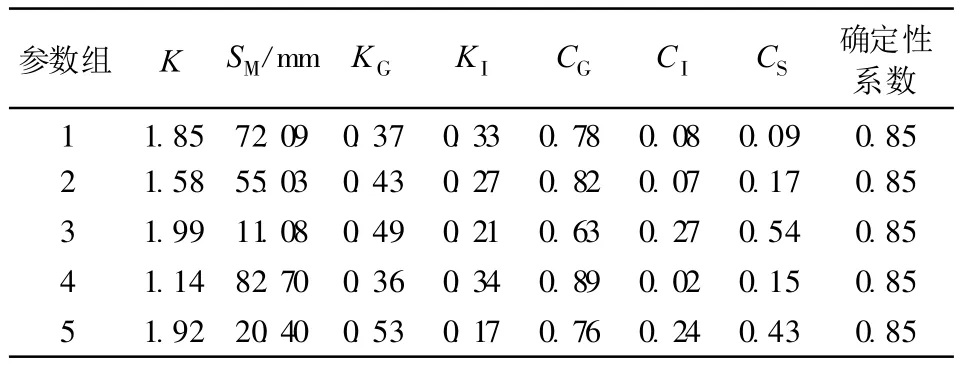
表2 东苕溪流域1983062308号洪水5组“等效性”参数组Table 2 Five groups of equivalent parameters of flood(No.1983062308)in Dongtiaoxi Catchment

表3 息县流域2002062120号洪水5组“等效性”参数组Table 3 Five groups of equivalent parameters of flood(No.2002062120)in Xixian Catchment

从表1和表2均可明显看出,同类参数在相同模拟似然值中的取值不同,有些参数如SM,CS变化很大,有些参数如K,KG,CG则变化较小,说明模型中每类参数的不确定性程度存在一定的差异.

3.3 参数不确定性分析

利用新安江模型对两个流域的洪水进行模拟,以确定性系数作为似然目标函数,得到参数与似然值散点分布图,据此可将参数归纳为以下3类.

第1类:不敏感参数.KG,KI,CG和CI这4个参数的似然值散点分布图在两个流域表现非常相似,都分布均匀,无明显的变化趋势,对确定性系数影响很小,属于不敏感参数.以KG为例,见图1.

第2类:敏感参数.从图2可以明显看出,参数CS的似然值散点分布图在两个流域分布区域的变化趋势相同,有明显的高值区,随着CS的增大确定性系数迅速下降,该参数对确定性系数影响较大,为敏感参数.

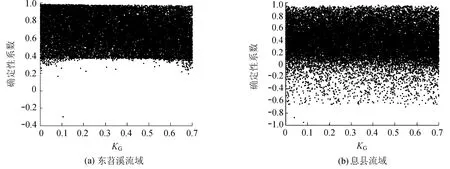
图1 不敏感参数与似然值散点分布Fig.1 Scatter distribution of likelihood values of non-sensitive parameters

图2 敏感参数与似然值散点分布Fig.2 Scatter distribution of likelihood values of sensitive parameters

第3类:区域敏感参数.K和SM的似然散点分布图在两个流域分布趋势有较大差别,同样的参数组合,在东苕溪流域分布均匀,在息县流域却有较明显的起伏变化.这体现了模型参数对流域水文特征不同的响应,东苕溪流域雨量丰沛,土壤水系发达,而息县流域土壤调蓄功能较差,由于面积较大,蒸发是水量平衡的主要因素.说明K和SM属于流域性敏感参数,敏感程度与流域水文气象特性密切相关.以SM为例见图3.

图3 区域敏感参数与似然值散点分布Fig.3 Scatter distribution of likelihood values of regionally sensitive parameters

3.4 模型预报的不确定性范围

设定似然判据确定性系数的临界值为0.8,低于该临界值的参数组似然值被赋为零,高于该临界值的所有参数组似然值重新归一化,然后,将模拟流量按大小排序,估算出一定置信度的模型预报不确定性的时间序列,求出90%置信度下新安江模型模拟的不确定性范围,即用累计似然分布的5%和95%两个分位点作为预测不确定性的界限.图4列出了东苕溪流域1983062308号洪水模拟的不确定性范围,其中包括实测值和不确定性的上限和下限.

从图4可以看出,不确定性范围与流量大小密切相关,在高流量区较大,低流量区较小.模型能够较好地模拟出流域出口断面的流量过程.同时,该场洪水模拟得到的90%置信度的流量过程未能包含所有的实测流量过程,说明参数的先验分布为均匀分布的假定不能满足要求,还需继续扩大参数的分布范围.

在GLUE方法中,使用贝叶斯公式更新似然值分布,参数组的数量逐渐减少,似然值的分布趋于稳定,可以得到稳定的似然值分布.初始经验揭示贝叶斯公式更新过程是逐渐减少那些后验似然值大于临界值的参数组数量,这说明随着考虑的实测资料越来越多,研究流域接受的参数组空间变得更加受约束,即参数不确定性因素会越来越小.在传统的模型参数率定中,一般率定出的参数组是唯一的,代表所有参数组收敛于一个最优参数组.而在GLUE方法中最优参数组不是唯一的,出现了最优模型参数解的集合.这是因为GLUE方法允许“最优”参数组可以随着观测值时刻变化,并且会反映在后验似然值分布的过程中.同时,GLUE方法允许在参数分布空间上存在不止一个区域的高似然值区,虽然总体趋势是由低似然值区域向高似然值收敛,但存在高似然值的却可以是多个区域,这同样也反映了模型的“异参同效”性.

GLUE方法允许使用者结合自己的模型来进行不确定性分析,后验似然分布可以直接用来评估没有实测值洪水事件的不确定性范围,本文利用没有用来更新似然分布的东苕溪流域1987071908号洪水对所构建的模型进行验证.由模拟结果图5可以看出,大部分的观测流量都落在了不确定范围之内,表明可以运用后验分布参数组来进行洪水预报,得到洪水发生概率及洪峰预报区间,这对于洪水概率预报具有较大的实践意义.

图4 东苕溪流域1983062308号洪水先验分布得到的不确定性范围Fig.4 Uncertainty ranges based on prior distribution of flood(No.1983062308)in Dongtiaoxi Catchment

图5 东苕溪流域1987071908号洪水后验分布得到的不确定性范围Fig.5 Uncertainty ranges based on posterior distribution of flood(No.1987071908)in Dongtiaoxi Catchment

4 结 语

以水文特性差异较大的东苕溪流域和息县流域为实例,运用GLUE方法对所购建的新安江模型参数不确定性进行了较为详细的分析.研究结果表明,两个流域都存在大量“等效性”参数,不同的参数组合能够模拟出相似的效果,充分验证了GLUE方法的中心观点:模型模拟效果是由参数组合决定的.根据两个流域的参数与似然值散点分布图,可将所研究的7个参数分为不敏感参数(KG,KI,CG,CI)、敏感参数(CS)和区域敏感参数(K,SM)3类.通过计算90%置信度的模型预报不确定范围,为进一步进行洪水概率预测提供技术支持.研究中发现,在给定参数分布和取值区间的条件下,实测流量并不能完全包含在该流量界限内,这是不确定性的表现,说明了参数的取值范围还需进一步扩大,同时也表明GLUE方法存在某些方面上的不足,需要对模型结构的不确定性进行更加细致的研究,以便完善和改进流域水文模型.

[1]夏军.现代水文学的发展与水文复杂性问题的研究[C]//第二届全国水问题研究学术研讨会论文集.北京:中国水利水电出版社,2004:3-18.

[2]KUCZER A G.Improved parameter inference in catchment models:1.evaluating parameter uncertainty[J].Water Resource Research,1983,19(5):1151-1162.

[3]赵人俊.流域水文模型的比较分析研究[J].水文,1989(6):1-5.(ZHAO Ren-jun.Comparative analysis of hydrologic modelof basin[J].Journal of China Hydrology,1989(6):1-5.(in Chinese))

[4]BEVEN K,BINLEY A.The future of distributed models:model calibration and uncertainty prediction[J].Hydrological Processes,1992(6):279-298.

[5]郭生练,李兰,曾光明.气候变化对水文水资源影响评价的不确定分析[J].水文,1995(6):1-5.(GUO Sheng-lian,LI Lan,ZENG Guang-ming.Uncertainty analysis of impact of climate change on hydrology and water resources[J].Journal of China Hydrology,1995(6):1-5.(in Chinese))

[6]李向阳,程春田,林剑艺.基于BP神经网络的贝叶斯概率水文预报模型[J].水利学报,2006,37(3):354-359.(LI Xiang-yang,CHENG Chun-tian,LIN Jian-yi.Bayesian probabilistic forecasting model based on BP ANN[J].Journal of Hydraulic Engineering,2006,37(3):354-359.(in Chinese))

[7]芮孝芳,刘方贵,邢贞相.水文学发展及其所面临的若干前沿科学问题[J].水利水电科技进展,2007,27(1):75-79.(RUI Xiao-fang,LIU Fang-gui,XING Zhen-xiang.Advances in hydrology and some frontier problems[J].Advances in Science and Technology of Water Resources,2007,27(1):75-79.(in Chinese))

[8]FREER J,BEVEN K.Bayesian estimation of uncertainty in runoff prediction and the value of data:an application of the GLUE approach[J].Water Resources Research,1996,32(7):2161-2173.

[9]FRANKS S W,BEVEN K J.Bayesian estimation of uncertainty in land surface-atmosphere flux prediction[J].Geophysical Research,1997,102(20):23991-23999.

[10]赵人俊.流域水文模型-新安江模型与陕北模型[M].北京:水利水电出版社,1984:33-42.

[11]ZHAO Ren-jun,LIU Xin-ren.The Xinanjiang model[C]//SINGH V P.Computer Models of Watershed Hydrology.Highlands Ranch,Colorado,USA:Water Resources Publications,1995:215-232.

[12]王佩兰,赵人俊.新安江模型(三水源)参数的客观优选方法[M].北京:中国水利水电出版社,1989.

[13]李致家.水文模型的应用与研究[M].南京:河海大学出版社,2008.

[14]李胜,梁忠民.GLUE方法分析新安江模型参数不确定性的应用研究[J].东北水利水电,2006,24(2):31-33.(LI Sheng,LIANG Zhong-min.Study on GLUE method applied to analyzing uncertainty of Xinanjiang model parameter[J].Water Resources&Hydropower of Northeast China,2006,24(2):31-33.(in Chinese))

[15]黄国如,解河海.基于GLUE方法的流域水文模型的不确定性分析[J].华南理工大学学报:自然科学版,2007,25(3):137-142.(HUANG Guo-ru,XIE He-hai.Uncertainty analyses of watershed hydrological model based on GLUE method[J].Journal of South China University of Technology:Natural Science Edition,2007,25(3):137-142.(in Chinese))