质量—弹簧振子系统的ANSYS有限元分析

黄兆梁

(常州工学院光电工程学院，江苏 常州 213002)

质量—弹簧振子系统的ANSYS有限元分析

黄兆梁

(常州工学院光电工程学院，江苏 常州 213002)

对质量—弹簧振子系统进行的ANSYS有限元模态分析，得出了与理论计算特征频率完全一致的结果。通过这种相互一致的印证，可以确信关于弹簧有效质量的理论计算公式是准确、可靠的。

模态频率;有效质量;质量—弹簧振子;振动

0 引言

对于弹簧质量不可忽略的质量—弹簧振子系统振动问题的研究国内外有许多报道[1-5]，多数都认为只要将弹簧质量的1/3加到振子质量上去，就可以将该振动系统等效看作无弹簧质量的理想振子系统，其振动周期为:

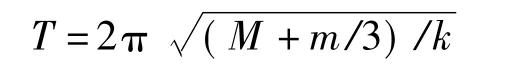
其中，M为振子的质量，m为弹簧质量，k为弹簧的弹簧系数。但进一步的理论研究揭示，当弹簧质量不可忽略时，质量—弹簧振子系统的振动并非简谐振动，也不属于严格的周期运动，而是准周期运动，其振动的模式有无穷多，各模式的振动频率之间也都不成有理数的倍数关系[6]。大量文献报道了各自从理论或实验的不同角度分析该振动系统而得出的不同结论。由于受实验技术等条件所限，实验精度都不足以给出与理论值之间高度吻合的有力证据，因此，对弹簧的有效质量问题并没有定论。有些文献对于弹簧质量1/3修正问题存有异议，或认为1/3仅仅是0.346的近似[7]，也有从各自的实验数据的分析中得出了该质量修正值的不同结论[8-10]，正所谓众说纷纭，莫衷一是。本文拟采用ANSYS有限元分析工具来分析质量—弹簧振子的振动模态，获得了与文献[6]高度吻合的结果，从而对解决弹簧的有效质量问题提供了具有相当说服力的佐证。

1 ANSYS有限元建模分析

有限元建模中质量单元采用了mass21，并定义为二维质量单元，弹簧采用combin14，并定义为二维纵向弹簧单元。作为对照与校验，同时也采用了beam3梁单元来模拟线性弹簧，不过梁beam3单元并不能直接输入弹性系数k，而需要通过输入弹性模量E，梁截面面积A，以及梁的长度L来实现梁单元的纵向(沿梁的长度方向)的弹性系数为k的目的。由于这里的梁并不用来作承重分析，且不需要用到梁的截面惯量矩，因此截面形状可以随意选取，方便起见，截面形状取正方形，边长都设为1 m，则面积为1 m2，梁的长度也设为1 m，在输入梁的弹性系数k时，在数值上已经与弹性模量E相同，从而可以将弹性系数k的数值直接输入到梁单元的弹性模量EX中，而泊松比直接以0填入到泊松比输入提示符PRXY相应的输入框中去。至于梁单元被设置为正方体及梁单元不作承重而作弹簧似乎不合常理的担忧是没有必要的，这样做只是为了ANSYS的材料特性参数设置的便利并确保分析结果的正确，况且由于有combin14弹簧单元作为参考印证，可以保证分析结果的准确、可靠。弹簧质量m可以通过对材料密度来进行设置，在这里可以直接将弹簧质量m的数值输入到密度输入提示框DENS中。分析中约束了除纵向振动之外的所有自由度，而固定端则需作全约束。为了检验ANSYS建模分析的有效性与可靠性，首先分析无质量弹簧的理想振子的情况，并与理论计算的结果相比较以检验两者相符的程度。为了计算方便，假定振子质量M=1 kg，弹簧的弹性系数k=1 N/m，由理论公式可计算得出其振动频率为:

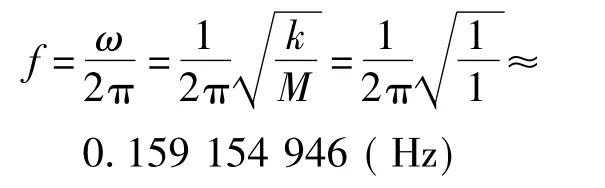
用梁单元beam3模拟无质量(m=0)及弹性系数k=1 N/m，振子质量M=1 kg的理想弹簧振子，无论将弹簧划分为多少个网格单元，其第一阶振动模态的频率都为0.159 15 Hz，这与理论值完全吻合。

用ANSYS的弹簧单元combin14来模拟弹簧就要简单得多，可以直接设置弹簧质量m和弹簧系数k，用其进行模态分析得出的理想弹簧振子的第一阶振动模态的频率也同样是0.159 15 Hz，两者没有任何差异。

虽然在模态分析中要求展开至30阶，而实际结果无论是采用combin14单元还是beam4单元都只给出了一阶振动模态，这意味着在这种情况下确实只存在唯一的一阶振动模态，而不存在其他的振动模态，这清楚地表明了理想弹簧振子的运动是属于简谐振动。ANSYS有限元分析所给出的5位有效数字与理论计算值是完全一致的。

对于一质量为m、弹簧系数为k的连续弹簧在作ANSYS分析时需将其分成均等的n段，每一小段连续弹簧都被看作一质量为m/n的集中质量与刚度系数为n·k的无质量小弹簧构成，由n个这样的离散小质量—弹簧振子组成的系统来代替原来的连续弹簧，经这样离散化处理后的情况与一个实际的连续的有质量的弹簧在力学特性上是基本等效的。当然，这里所分的段数n越多就越能精确模拟实际的连续弹簧，稍有影响的是这个小的集中质量是该放置在小弹簧的什么位置，为此在分析中作了2种极端情况的处理，即将小弹簧的集中质量分别放置在小弹簧离振子较远一端和较近一端，并分别称之为远振子端和近振子端。分析结果显示，在这2种情况下相同阶的模态频率存在着少许差异，这种差异可以作为ANSYS的分析精度的一种衡量尺度，可以反映出分析的精度，而正确的模态频率应该介于2种极端情况之间。为了能够清楚地展示ANSYS的分析精度随划分的单元数的变化情况，本文将弹簧划分成了100、1 000和10 000个单元的离散质量—弹簧振子，每种情况下又可分为“远振子端”与“近振子端”两种极端情况，并分别用“+”、“-”附在所划分的单元数之后作为标记。

2 模态分析结果

采用ANSYS的APDL语言进行简单的编程，将振子质量M、弹簧质量m、弹簧弹性系数k、弹簧划分单元数n均作为输入参数，通过在输入界面上更改这些参数就可以很方便地对不同参数的情况进行反复计算。经过上述的ANSYS仿真分析后，即可求解得出各模态的振动频率。这里针对combin14和beam3单元分别编写了两段程序，在将弹簧分别划分为100、1 000和10 000等份的情况下，对振动模态进行有限元仿真分析，其中对弹簧单元combin14还需区分远振子端与近振子端2种情况，其前30阶振动模态的振动频率以及理论计算值见表1。

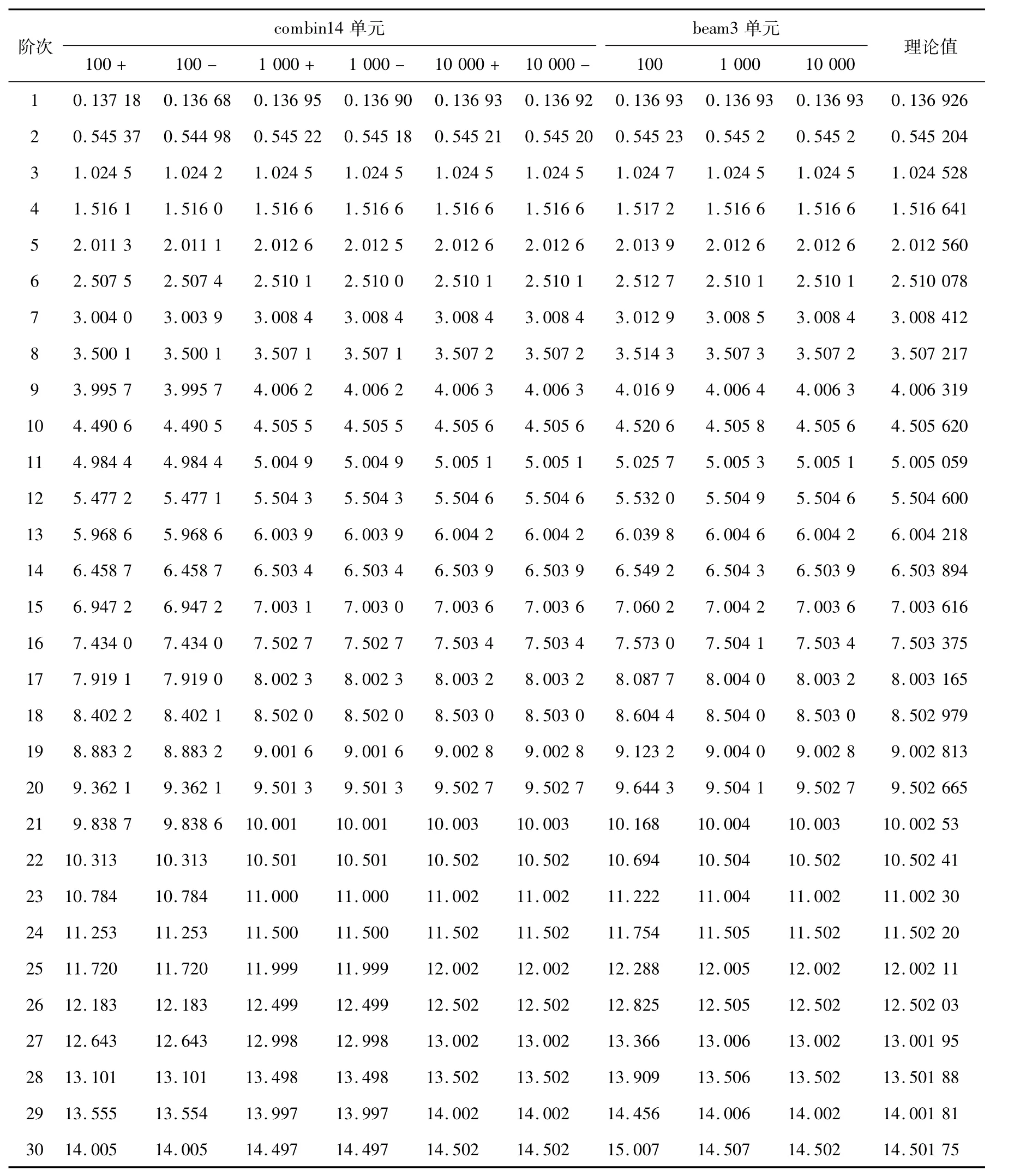
表1 ANSYS计算值与理论值的比较(M=1 kg，m=1 kg，k=1 N/m，combin14与 beam3 单元)

由表1可见:

1)ANSYS计算值与理论值非常吻合，尤其是当划分单元数较多时，ANSYS所给出的5位有效数字与理论计算值无差异。

2)当弹簧质量偏置于远振子端时频率偏高;而当弹簧质量偏置于近振子端时频率偏低;其平均值更为接近理论值。

3)相比而言，远振子端情况的数据要比近振子端情况的数据略为准确一些。这是由于弹簧质量的一级修正值为弹簧质量的1/3。

4)采用梁单元beam3来计算振动模态比用combin14单元更为准确，其收敛于理论值的速度更快、效果更好，也不用区分远振子端还是近振子端。但在无理论值的情况下不便于精度估计。

对于一阶振动模态，表2给出了采用Mathematica7.0根据文献[6]各级修正公式计算得出的近似频率、理论值及其相应的相对误差。

表2 一阶振动模态各级修正公式的精度

随着计算公式的修正级次的增加，通常计算精度也越高，但修正级次过高会出现“振荡”，适当选取修正级次可获得较好效果。表2中的理论值是根据文献[6]中的式(8)计算得到的，其五级(原文献[6]式(11)中 ω1(4)为 ω1(5)之误，即所给公式为一阶振动模态ω1的五级修正而非四级修正。)振动频率修正是根据文献[6]中的式(11)的角频率计算得出，即:

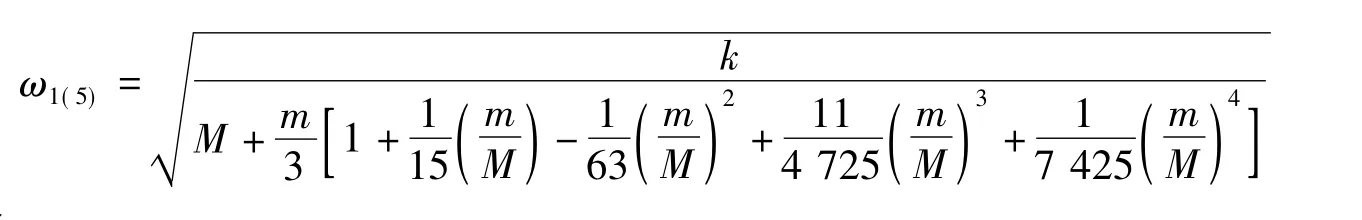
而四级修正为:

其余可依次类推。

值得注意的是，当采用beam3单元来对上述质量—弹簧振子系统进行模态分析时，如果将弹簧单元仅仅划分为一个单元时，这时的质量—弹簧振子系统就仅仅只有一个自由度，因此其得出的振动模态就仅仅只有一阶，其频率为0.137 83 Hz，正好与表2中的一级修正公式也即1/3弹簧质量修正公式得到的振动频率完全相同，这并不是偶然的巧合。事实上，如果将弹簧单元仅仅划分为一个单元，这就意味着弹簧被限制为只能作均匀的线性伸缩变化，而不能作疏密相间的弹性波动的变化。众所周知，1/3的弹簧质量修正的公式的推导正是建立在弹簧仅仅作均匀的线性弹性伸缩变化的假定之下推导而得到的结论，因此，这里两者结果完全相同也是在意料之中。一般情况下弹簧的伸缩并不是线性变化的，而是呈现出比较复杂的波动，这正是存在无穷多振动模态的原因所在。

3 结论

由ANSYS仿真得出的各阶振动模态的频率与由本征值方程[6]ytany=β求解得出的对应特征频率完全一致，这就充分说明将连续弹簧视作均匀的连续介质，用波动方程来描述弹簧的振动是行之有效的，并且具有相当高的精度，能够相当精确地描述弹簧振子在振动过程中由弹簧引起的波动现象。另外，在认可ANSYS分析的结果是准确、可靠的基础上，那么也就能验证文献[6]中的式(11)所求出的振动模态的正确性，而作为其中一阶振动模态的弹簧有效质量的计算公式自然也就是准确无误的。

通过理论分析与有限元分析结果吻合一致的相互印证，可以有充分理由来终结有关弹簧有效质量到底该如何准确计算的长期悬而未决的争议，也能充分理解为何通过实验来进行弹簧有效质量检验的种种努力始终都未能给出令人信服的结果。

[1]丁履成，司明扬.有质量的弹簧的振动问题[J].大学物理，1985，4(9):15 -18.

[2]罗蔚茵.关于弹簧振子固有频率的进一步讨论[J].大学物理，1985(11):9-11.

[3]Leclerc M.振动弹簧的有效弹性常数和有效质量[J].李国强，译.大学物理，1990，9(6):10 -11.

[4]刘大鹏，关荣华.弹簧质量对弹簧谐振子圆频率的影响[J].大学物理，1995，4(10):22 -24.

[5]Nune da Silva J M.负荷弹簧的重整化振动研究[J].孙厚谦，洪林，译.大学物理，1995，14(10):28 -30.

[6]黄兆梁.弹簧质量对振动的影响[J].大学物理，1998，3(17):12-16.

[7]陈美华，蒋毅.弹簧振子计及弹簧质量的误差分析[J].嘉应学院学报，2006，24(6):27 -30.

[8]刘伟.用振动法研究弹簧振子的有效质量和倔强系数[J].实验技术与管理，2006，10(23):38 -39.

[9]孙彦清.小振动系统弹簧质量影响因子的测量[J].汉中师范学院，2003，6(21):50 -52.

[10]肖波齐.基于Matlab的弹簧振子简谐振动研究[J].陕西科技大学学报，2009，12(27):116 -120.

The ANSYS Finite Element Analysis of Mass-spring Oscillator System

HUANG Zhao-liang

(School of Photoelectric Engineering，Changzhou Institute of Technology，Changzhou 213002)

This paper applies ANSYS modal analysis to the mass-spring oscillator system to obtain the modal frequency，whose results are in exact accordance with those eigen frequency calculated by the theory.The consensus of support each other can make sure that the effective quality of the formula is accurate and reliable.

modal frequency;effective mass;mass-spring oscillator;vibration

O326;O241.82

A

1671-0436(2011)02-0038-04

2011-04-02

黄兆梁(1956— )男，副教授。

责任编辑:张秀兰