基于鲁棒反馈线性化的船舶航向鲁棒内模控制

蔡旭东，曲 丰，崔滋刚，李 昌

(海军91388部队92分队，广东 湛江 524022)

基于鲁棒反馈线性化的船舶航向鲁棒内模控制

蔡旭东，曲 丰，崔滋刚，李 昌

(海军91388部队92分队，广东 湛江 524022)

针对具有不确定项的船舶航向非线性数学模型，结合鲁棒反馈线性化方法和鲁棒内模控制算法设计出了船舶航向的鲁棒内模控制器。该方法先将船舶航向非线性数学模型鲁棒线性化，在补偿型船舶航向鲁棒控制律的基础上，设计出内模控制算法。鲁棒内模控制器中的反馈滤波器可以抑制参数摄动引起的实际输出与模型输出的误差，并对相关参数进行在线校正。以某船为例，利用Matlab/Simulink工具箱进行仿真研究，结果表明所设计的鲁棒控制器具有较好的控制性能，对风浪干扰也具有很强的鲁棒性。

船舶航向控制;非线性系统;内模控制;鲁棒线性化

0 引言

航向控制是控制理论应用较早且取得成果较好的一个领域。自20世纪60，70年代以来，随着我国船舶航运事业的发展，船舶航向控制系统的控制与设计呈现出很大需求，发展也非常迅速，各种新的控制算法逐渐替代了传统PID控制。船舶在大洋航行时受到各种环境干扰和航行工况影响，船舶运动表现出非线性、不确定性、大滞后等复杂的动态特性，船舶运动的控制也表现为复杂的控制问题［1－2］。为了提高控制精度，针对船舶航向的非线性不确定性模型，研究鲁棒性强的船舶航向控制器设计方法是目前船舶运动控制领域的一个研究热点。

作为鲁棒控制之一的内模控制，能同时兼顾系统的鲁棒稳定性和控制性能，且只需对一个参数进行调整，整定方便、在线设计比较容易，且对纯滞后有补偿作用，一直受到工程界的重视［3－4］。本文针对具有不确定项的船舶航向非线性数学模型，根据不确定项与状态输入的匹配型条件，对其进行线性化处理，并采用补偿型鲁棒控制律来设计船舶航向控制律。通过鲁棒内模控制器中的反馈滤波器，抑制参数摄动引起的实际输出与模型输出的误差，并对相关参数进行在线校正。以某船为例进行仿真研究，结果表明所设计的鲁棒控制器具有较好的控制性能，对风浪干扰也具有很强的鲁棒性。

1 系统描述

在船舶运动中，由于航行中船速、装载状态等都是变化的，同时还受风流浪等外界干扰的作用，会引起参数的摄动，因此控制系统设计中模型可采用下列具有不确定性项的Nomoto模型:

式中:H(ψ)=α0+α1ψ+α2ψ2+α3ψ3;αi(i=0，1，2，3)为Norrbin系数;K，T为操纵性指数。由装载变化和风力等引起的ΔT，ΔK为参数不确定性项，其估算较为复杂，本文考虑航速变化ΔV引起的参数摄动，令

取状态变量x1=ψ，x2=ψ=r，u=δ为输入舵角，y=x1为输出。船舶航向非线性系统的关系度等于系统的阶数，是单输入单输出仿射非线性系统，则船舶航向非线性模型可表示如下仿射型不确定非线性系统形式:

又根据匹配型条件式有:

其中分离项有:

上述船舶模型为匹配型模型。当 Δf(x，p)=Δg(x，p)=0时，有α0=α2=0;该船舶航向非线性系统模型为标称模型。

2 鲁棒控制器设计

本文针对具有不确定项的船舶航向非线性数学模型，根据不确定项与状态输入之间的匹配型条件，对其进行线性化处理，并采用补偿型鲁棒控制律来设计船舶航向控制律。通过鲁棒内模控制器中的反馈滤波器，抑制参数摄动引起的实际输出与模型输出的误差，并对相关参数进行在线校正。

2.1 鲁棒线性化［5－6］

根据式(3)的标称系统，各阶李导数有:

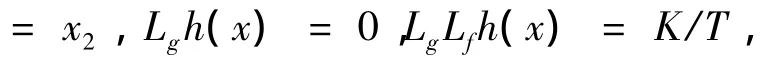
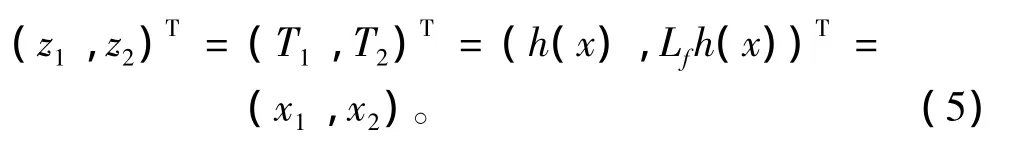
结合式(4)，可以推导出:

采用补偿型控制律:

2.2 鲁棒控制律设计

首先取外部控制输入为外部输入vd、极点配置K—z和补偿器vs之和，即:

式中:为极点配置的正常数列向量;vs为1个反馈型补偿器;q=［q1，q2］为在线调节参数，是标量常数，具有如下形式:

式(9)的表示形式并不惟一，这里它用只带有2个调节参数的简单结构来补偿控制系统的不确定项。结合式(6)～式(8)，可以得到:

进一步转换为可控制形式:

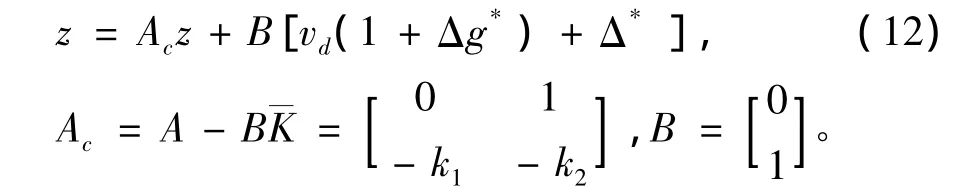
2.3 稳定性分析

下面将利用Lyapunov函数法分析上述船舶航向非线性鲁棒控制系统的稳定性。

取Lyapunov函数法为:V=zTPz。其中P为实对称正定矩阵。沿着式(12)所示函数的轨迹求微商可得到:

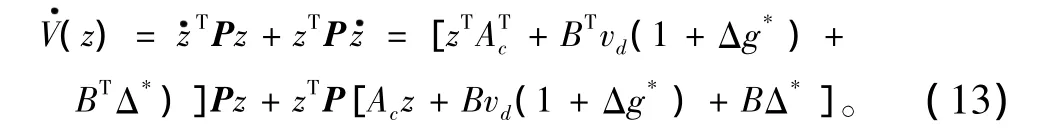
考虑式(12)中(Ac，B)为完全能控型，则有对称正定矩阵Q，使得:

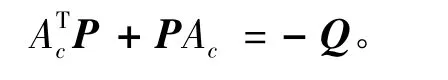
代入式(13)得:

则式(15)化为:

因此，适当地选择矩阵Q和参数q=［q1，q2］，可以使得V(z)≤0。经过上面的推导分析可知，通过适当选择参数来设计补偿器vs(x，q)的方法，大致抵消掉闭环系统的不确定项，但选择参数［q1，q2］有很大的灵活性。内模控制是鲁棒控制器设计的一种新型控制方法，具有良好的跟踪性能和抗外扰能力［7－8］。下面在补偿器vs的基础上，引入鲁棒内模控制(IMC)的方法来在线整定回路参数，在滤波器的作用下抑制系统输出误差y－ym的影响，增强系统的鲁棒稳定性，保证系统输出有效地跟踪期望输出。

图1中，ym为内模模型输出，Gc为内模控制器，Gf=1/(λs+1)2为反馈滤波器，Gm为内模模型:

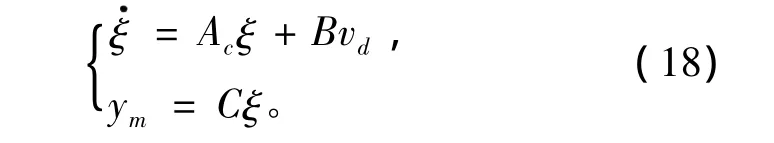
内模控制器

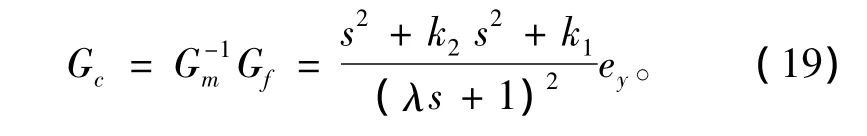
基于内部模型和反馈滤波器设计的内模控制律为

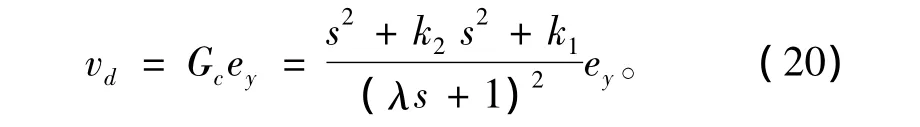
式中:ey=yE－(y－ym)Gf，yE为期望输出;λ为滤波器常数参数。

3 仿真

以某船为例进行仿真实验研究［2］，仿真参数有:船长L=126 m，船宽B=20.8 m，满载吃水d=8.0 m，方形系数Cb=0.681，航速V=7.7 m/s，T'=12.77，K'=8.12。通过计算可得K=K'V/L=0.4963，T=T'L/V=208.91，Norrbin 系数 α1=1，α3=30，KE=1。各设计参数相应取:K—=［0.07，0.001］T，改变航向角 ψ=+20°。

取滤波器系数λ=6，在标称模型下，q取不同值时得出的航向和舵角的输出曲线见图2和图3所示。

取q=［1，10］时，在标称模型下，λ取不同值时得出的航向和舵角输出曲线见图4和图5所示。

只考虑参数摄动时，不同参数摄动下航向角的输出曲线见图6所示。当同时取摄动p=－1/3，λ=1，q=［1，10］，将风、浪等干扰的影响等效成正弦和随机信号加入到舵角输入进行仿真，得到的航向输出曲线见图7和图8所示。

根据仿真结果图2和图3，可以分析出在滤波器系数λ不变的情况下，补偿器vs(x，q)的参数q=［q1，q2］的选取可以影响到船舶航向控制系统输出的超调量和调节时间。随着q1的增大，航向角和舵角的超调量由无到有，并逐渐增大，调节时间也越长。而随着q2的增大，航向角和舵角的超调量逐渐减小，且调节时间越短。从图4和图5可以看出，在补偿器参数不变的情况下，滤波器系数的选取也同样影响到船舶航向控制系统输出的超调量和调节时间。随着λ的增大，航向角和舵角的超调量逐渐减小，但调节时间更长。从仿真图6～8可以看出，外界干扰信号对船舶航向影响较小，舵角和首摇角速度的输出较稳定，出现的超调也在航向自动舵的控制性能指标以内。仿真实验表明，采用基于鲁棒线性化的鲁棒内模控制算法可以有效地跟踪、保持船舶航向，对外界干扰和模型摄动具有较强的鲁棒性。

图8 参数摄动和风浪扰动下的舵角输出曲线Fig.8 The output characterisitic curve of ship's rudder angle under different parameter perturbation and wind wave interference

［1］DO K D，JIANG Z P，PAN J.Robust global stabilization of under actuated ships on a linear course:state and output feedback［J］.Int.J Control，2003，76(1):1 －17.

［2］孔令涛，杜佳璐，王玉杰.基于逆推非线性阻尼算法的船舶航向控制器设计［J］.大连海事大学学报，2006，32(4):61－64.

KONG Ling-tao，DU Jia-lu，WANG Yu-jie.Ship steering controller design based on backstepping algorithm and nonlinear damping algorithm［J］.Journal of Dalian Maritime University，2006，32(4):61 －64.

［3］周涌，陈庆伟，胡维礼.内模控制研究的新发展［J］.控制理论与应用，2004，21(3):475 －482.

ZHOU Yong， CHEN Qing-wei， HU Wei-li. New developments of research on internal model control［J］.Control Theory ＆ Applications，2004，21(3):475 －482.

［4］赵曜.内模控制发展综述［J］.信息与控制，2000，29(6):526－531.

ZHAO Yao.A survey of development of internal model control［J］.Information and Control，2000，29(6):526 － 531.

［5］CHOU Yi-Shyong，WU Wei.Robust controller design for uncertain nonlinear systems via feedback linearization［J］.Chemical Engineering Science，1995，50(9):1429 －1439.

［6］SASTRY S.Nonlinear systems［M］.北京:世界图书出版公司北京公司，2007.417 －422.

［7］潘立登.先进控制与在线优化技术及其应用［M］.北京:机械工业出版社，2009.123 －134.

［8］HU Q，SAHA P，RANGAIAH G P.Internal model control with feedback compensati-on for uncertain nonlinear systems［J］.Int J Control，2001，74(14):1456－1466.

Robust internal mode control for ship autopilot based on robust feedback linearization

CAI Xu-dong，QU Feng，CUI Zi-gang，LI Chang(92 Unit of 91388 Naval，Zhanjiang 524022，China)

In allusion to the nonlinear uncertain ship model，a robust internal mode controller for ship autopilot was put forward by using robust feedback linearization technique and robust internal mode control algorithm.The feedback filter in robust internal mode control was employed to dispel the error caused by parameter perturbation between model output and anticipant output，where the parameters were on-line tuned.The simulation results based on the Matlab/Simulink package showed that the effectiveness of the designed controller.It can track the desired course accurately and exhibit strong robustness peculiarity to the uncertainties of nonlinear ship model.

ship autopilot control;nonlinear system;internal model control;robust linearization

TP273;U664

A

1672－7649(2011)12－0037－05

10.3404/j.issn.1672－7649.2011.12.008

2011－01－04;

2011－03－04

蔡旭东(1985－)，男，硕士，助理工程师，主要研究领域为信号探测处理与系统控制、系统试验航路航向设计与优化等。