基于蒙特卡罗法的电磁齿轮的可靠性分析

倪 涛

（黄冈职业技术学院，黄冈 438002）

0 引言

磁力机械已经成为了国内外研究的热点，电磁齿轮属于一种新兴的磁力机械，其工作原理就是磁性耦合，通常情况电磁齿轮通过非接触形式完成传动任务，相对于传统齿轮，电磁齿轮的传动特性更加优秀，比如，不用采用润滑手段，没有摩擦和磨损，对环境没有污染，同时没有振动和噪声。电磁齿轮是以现代电磁理论为依据的，通过电磁铁或永磁材料形成磁力，从而能够保证电磁齿轮能够以非接触的形式实现力或力矩的传递。电磁齿轮的每一个轮齿的极齿都具有N极或S极磁性，全部的极齿分布在电磁齿轮的外圆面上，N极和S极通常情况下都是配对使用的，一个N极和一个S极就可以构成一个极对，当将直流电接入线圈以后,磁通左端沿轴向通过导磁铁芯、与左极齿相对应的法兰经过左极齿部，就构成了N极；右端磁通通过直流线圈的导磁环经过右极齿的环圈最后流经右极齿部,最终构成了S极。

当保持激励电压不变的条件下，提高电磁齿轮线圈内的电流值，就会相应地增强磁感应强度，进而能够增加电磁齿轮的电磁吸力，然而，按照牛顿冷却定律，电磁齿轮线圈的温升和电磁齿轮线圈内的流通电流的平方是服从正比例的关系，所以，电磁齿轮线圈内的流通电流的提高同时会导致线圈的温度增加，发出更多热量，如果在电磁齿轮的设计阶段没有充分地考虑线圈的散热问题，就容易线圈的温度过高。一旦电磁齿轮的温度超出了设计温度，电磁齿轮的绝缘材料就将老化，电磁齿轮的可靠性不断地降低，从而极大地减小了电磁齿轮的寿命，因此电磁齿轮的控制电流是电磁齿轮安全平稳运行的关键。

可靠性设计可以考虑参数的不确定性，能够以可靠度或其他可靠性的指标作为评价标准，使设计更加合理，传统的可靠性分析都是以大样本实验数据为依据，而电磁齿轮电磁力和热性能可靠性仅仅能够依据小样本的实验数据，从而会导致分析结果和实际情况不相符合。蒙特卡罗模拟法能够对电磁齿轮的热性能的变化规律进行模拟计算，接着，根据电磁力和热性能的变化规律进行可靠性指标的计算，并且进行敏感性研究。

1 蒙特卡罗法概述

蒙特卡罗法属于一种计算机模拟技术，也可以被称为统计模拟实验技术法或随机模拟技术，目前该方法已经被成功地应用于各个工程领域之中，属于一种基于统计理论的对工程中的数学或物理问题进行近似计算的手段，蒙特卡罗法的主要思路为：第一步，根据工程问题的实际情况建立一个能够充分反映实际问题的随机过程或概率数学模型，所建立的数学模型的数学期望或概率分布也就是欲求问题的解；第二步，通过对所建立的概率模型或随机过程模型进行抽样统计从而最终确定所求解的参数的概率分布；最后，能够求解出概率模型的近似值。这样就能够有效地解决工程中的数学或物理问题。

蒙特卡罗法的原理如下：按照大数定律，设有m个相互独立的变量，分别为x1,x2,…,xm，这n个变量是同一母体中的独立变量，分布均一样，同时具备一致的均值与方差，可以由字母µ与σ2来标识，这样针对任何的ε＞0都满足以下条件：

2 灵敏度分析概述

灵敏度分析就是随着系统的输入改变，系统的输出随之而变的敏感性的强弱。利用灵敏度分析能够有效地反映概率模型中不同的参数对系统的输出的敏感程度。利用灵敏度分析，能够发现系统的设计变量对目标函数的敏感程度。

目标函数对设计变量的灵敏度代表了设计变量的轻微改变导致目标函数的变化情况，目标函数表示为以下形式：

依据隐函数定律，输出变量对输入变量的灵敏度可以表示为如下的形式：

式中，xn表示第n个输入变量。

某系统含有三个相互耦合的子系统，相应的耦合矩阵如下所示：

其中：y1、y2、y3表示了系统所包含子系统的输出；I表示了单位阵；公式(4)中右侧的向量代表了局部灵敏度，局部灵敏度的含义是当其余影响没有改变时，不同子系统对输入变量的敏感性；公式(4)的左侧的矩阵代表了全局灵敏度，其含义是不同子系统对其余子系统输出的敏感性；公式(4)左侧的向量表示了系统灵敏度，其含义是系统输出变量和系统输入变量的灵敏度所对应的导数，由于不同子系统之间存在着耦合关系。公式(4)表明，局部灵敏度以及全局灵敏度间是经过系统灵敏度向量而相互关联起来的，系统灵敏度向量包括了系统全部输出对任何输入变量的灵敏度，同时导数中也表明了不同子系统间的耦合关系。

3 基于蒙特卡罗法电磁齿轮电磁力和热性能的可靠性分析流程

1）确定电磁力和温升的函数y=f(x1,x2,…,xm)，并且确定出随机变量x1,x2,…,xm。

2）确定电磁力和温升函数中随机变量xn所对应的概率密度函数f(xn)。

3）确定电磁力和温升函数中随机变量xn所对应的累积分布函数F(xn)。

4）概率密度函数中的随机变量形成一个遵循均匀分布的数列Wxij，其表达式如下所示：

式中，i表示随机变量的序号，i=1,2,…,m；j表示蒙特卡罗模拟的次数，j=1,2,…,103。xij表示了随机变量xi经过第j次模拟计算以后获得的一组伪随机数。

5）将各组伪随机数xij代入电磁力和温升的表达式中，可以获得yi。

6）经过j模拟计算，获得电磁力和温升的每次函数大小，进行升序排列。

7）绘制y的直方图，拟合直方图的分布。

确定了电磁力和温升的分布以后，利用蒙特卡罗法模拟出电磁齿轮的电磁力和温度耦合的可靠度。

4 电磁齿轮电磁力和转矩的计算方法

电磁齿轮的磁感应强度由于电磁齿轮的漏磁通而不一样，因此，在分析的过程中可以将分析区域划分为若干小区域，提出每个小区域的磁感应强度相同的假设，则磁场能量可以表示为以下的形式：

式中，Bi表示了磁感应强度；Hi表示了磁场强度；Vi表示了气隙的体积；Ai表示了气隙的横截面面积；Si表示了空气气隙。

对应的磁场力的计算公式如下所示：

式中，Fi表示了每个小区域的磁场力。根据安培定律可得：

联立公式(7)和公式(8)，电磁齿轮的电磁力和转矩可以分别表示为：

式中，µ表示了真空磁导率；I表示电流强度；N表示了线圈匝数；D表示爪极的直径，NP表示磁极数。

最后，利用电磁场分析获得的焦耳热转化为电磁齿轮的温升。

5 基于蒙特卡罗法电磁齿轮电磁力和热性能耦合可靠性分析

表1 电磁齿轮电磁力四组蒙特卡罗模拟计算结果

图1 电磁齿轮电磁力的频率分布结果图

利用蒙特卡罗法计算出电磁齿轮的电磁力的概率分布，通过计算可得近似符合正态分布，表1给出了四组电磁齿轮电磁力的计算结果。图1给出了四组电磁力的数据模拟结果的频率分布结果图。

利用蒙特卡罗法计算出电磁齿轮的温升的概率分布，计算结果表明电磁齿轮温升的概率分布比较接近于对数正态分布，表2给出了4组电磁齿轮温升的计算结果。图2给出了电磁齿轮4组温升的概率分布结果图。

表2 电磁齿轮的温升四组蒙特卡罗模拟计算结果

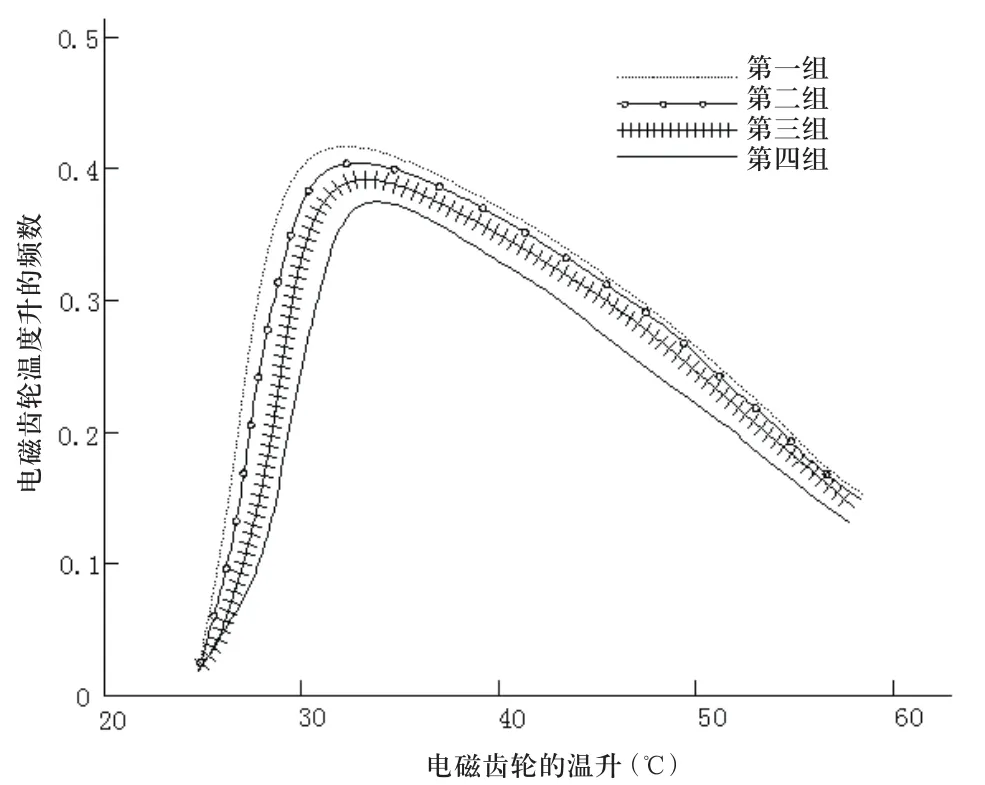
图2 电磁齿轮温升的频率分布图

表3给出了蒙特卡罗法的可靠度计算结果，从表3可以看出，当模拟结果超过2×104次的时候，可靠度的数值已经收敛。

表3 电磁齿轮可靠度模拟结果表

6 基于灵敏度的电磁齿轮可靠性分析

灵敏度分析利用蒙特卡罗法进行模拟计算，预先定义灵敏度分析的模拟次数为25次，经过灵敏度分析获得的结果如表4所示。从表4可以看出，电磁齿轮的温升比电磁齿轮的电磁力对电磁齿轮的可靠性影响更大。

表4 灵敏度分析结果

7 结论

电磁齿轮属于一种新型的非接触机械，其电磁场和温度场的耦合计算是电磁齿轮设计的基础，电磁力和温度场对电磁齿轮的可靠性具有非常重要的影响，利用蒙特卡罗法对电磁齿轮进行可靠性分析，能够避免传统可靠性分析中需要大量实验样本的缺陷，具有较好的鲁棒性。

[1] 周哲波,章宏令.基于蒙特卡罗法的高压容器可靠性分析[J].煤矿机械,2010,31(12):99-101.

[2] 郭水旺,胡乾坤.基于蒙特卡罗的电子产品可靠性分析[J].电子与封装,2010,10(5):33-35.

[3] 任文杰,王伟,王丽君,等.蒙特卡罗仿真在飞控系统可靠性评估中的研究[J].计算机仿真,2009,(4):63-66.

[4] 张道兵,朱串曲,刘泽,等.基于Matlab优化工具箱的煤巷顶板锚杆支护结构可靠性分析[J].中国安全科学学报,2007,17(9):131-134.