灰色理论在围岩变形预测中的应用

解志刚 许海东

1 概述

在预测分析中，最基本的是线性回归预测，但是在实际工程应用中，我们的数据是非线性的、离散状态的，隧道围岩的变形就是一个由复杂因素所决定的非线性的变形，对于隧道围岩变形的预测中线性预测办法是不可取的，我们可以应用灰色理论对围岩的变形进行预测。灰色理论，又称灰色系统，是指既有已知信息，又包含未知信息的系统;是研究分析、建模、预测、决策、控制的理论。该理论自20世纪80年代创立以来，已经在社会科学和自然科学的许多领域得到了应用。岩石力学中的一些问题，例如上述围岩变形，具有灰色系统的特点，灰色理论能很好的应用于上述问题。以下将讨论利用灰色理论进行围岩变形的预测。

2 灰色理论的GM(1，1)模型

围岩变形的测量结果，是一个时间序列数据，通过建立灰色理论模型，来预测未来围岩变形，以便为工程的设计和施工提供有关的围岩动态信息。首先讨论GM(1，1)模型问题。

2.1 建立 GM(1，1)模型

假定在时间序列 t1，t2，…，tn，量测的围岩变形为数列 x1，x2，…，xn，记为:

此为原始数据，为了弱化原始数据的随机性，对原始数据做累加，也就是它的1-AGO，得到数列:

由原始数据(1)和累加数据(2)可以分别得到向量Y和矩阵B:

对于GM(1，1)模型，相应的白化微分方程为:

该微分方程的解为:

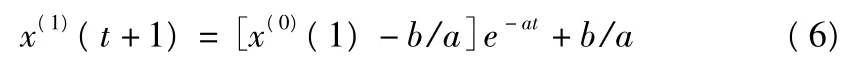
其中，a，b均为待定系数，一般记为 A=［a，b］T。

对于微分方程(5)，其待定系数A=［a，b］T的最小二乘法解为:

将原始数据x(0)(i)和累加数据x(1)(i)代入式(7)中，可以得到a，b值。我们可以通过式(6)进行预测。

2.2 GM(1，1)模型的精度

以上我们介绍了灰色理论模型的建立方法，下面我们要根据解式(6)计算残差:

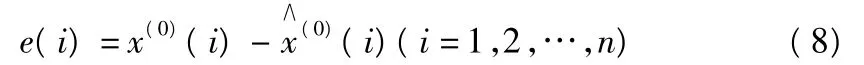
得到残差向量和相对误差分别为:

设原始数据的方差及残差向量的方差分别为s21和s22，则:

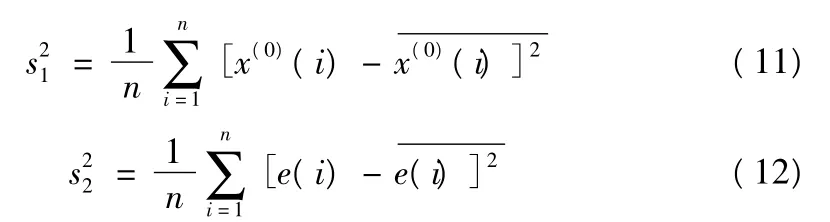
方差比值Q为:

小误差概率为:

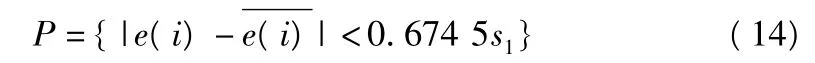
模型的精度由Q和P来控制和表述，一般将其分成四级，见表1。通过计算所得P值或Q值来划分等级，评价预测精度的好坏。

表1 预测精度等级划分

2.3 基于灰色预测的等维灰数替补迭代

为了进一步提高模型预测的精度，在灰色模型的基础上还可以做进一步的改进，使得预测结果更加准确。GM(1，1)模型具有预测意义的数据仅仅是x(0)(i)以后的前几位数或者∧x(0)(i)数列的前几位数，随着时间的推移，旧的数据越来越不适应新的情况，所以，要在原数据的基础上每次增加一个新信息时，就去掉一个旧信息。这种新数据补充、旧数据除掉的数列，由于维数没有变，因而叫等维灰数数列或者叫新陈代谢数列。利用新的数列重新建立GM(1，1)模型，对下一个新数据进行预测，预测完毕后，再次生成新的数列。这样就类似于迭代原理，我们可以通过数值计算来实现GM(1，1)模型的生成和迭代，这样的改进可以保证精度的良好性。

3 利用GM(1，1)模型预测隧道围岩的变形

以武广高速铁路衡阳段胡子冲隧道为例，隧道的围岩以花岗岩为主，地下水丰富，地形比较复杂。隧道初期支护的喷射混凝土厚度为25 cm，我们在隧道开挖过程中对DK091+124断面拱顶围岩变形进行了监测，监测数据见表2。

GM(1，1)模型的建立，是在取得一定数据之后进行的，建模以后就可以对未来变形进行数据预测。由于收敛变形是持续进行的，因此，不断有新的数据充实变形时间序列，考虑到现场的条件不断变化，前期测量的数据对后期研究围岩的变形有一定的作用，但是越是接近于预测时间的量测数据越有意义(见表3)。因此，我们采用GM(1，1)迭代模型来进行预测，预测后我们可以对预测和实测数据进行比较(见图1)。

图1 实测与预测数据对比图

表2 监测数据

表3 GM(1，1)模型的预测值

经过对残差的计算，本例中的GM(1，1)模型的精度达到了Ⅰ级，所以预测的数据与实际数据还是比较吻合的。

通过计算我们可以判断在4 d以后围岩稳定，在50 d左右变形加大，这时胡子冲隧道进尺达到56 m，应该进行二次支护或者应停止开挖，以保证隧道施工的安全。同时我们使用有限元软件对胡子冲隧道进行了施工模拟，通过模拟可以知道在隧道进尺60 m左右时必须进行二次支护，模拟过程这里不再赘述。从这里可以看出利用灰色理论进行隧道围岩变形的预测在实际工作中是有很大意义的。

4 结语

本文通过以胡子冲隧道的围岩变形预测为例，对灰色理论在围岩与初期支护相互作用变形预测的应用进行了阐述。灰色系统理论有着广泛的应用前景，将其用于分析和处理围岩的变形预测是一种行之有效的方法。通过上述分析和论述，我们可以得出以下结论:

1)利用GM(1，1)模型对变形进行预测方便之处是实测数据需要很少(灰色理论并不因为实测数据多而变得精确度高)，并且预测数据的精度高，对于普通回归方法则要更多的数据来预测，而且灰色理论能对一些非线性或者不确定的因素进行弱化，以提高预测的准确性。2)收敛变形的时效性动态表明，预测变形必须时时更新，而灰色理论预测恰恰能解决这个问题，这与以往回归方法不同，这样能更加有利于隧道施工中的变形监控(施工要求时时监测围岩变形，已确定围岩变形的稳定情况)。3)从取得原始数据到建立GM(1，1)模型，计算量还是比较大的，但是我们可以在计算机上利用数值计算方法轻松完成建模和迭代计算。因此，用灰色理论来分析围岩变形资料，预测围岩收敛变形以及判断可能失稳的前兆及时间是有工程实用意义的。

［1］ 张忠亭，陶振宇.洞室围岩收敛变形的时间效应特性研究［J］.武汉水利水电学院学报，1995(12):89-92.

［2］ 邓聚龙.灰色系统理论教程［M］.武汉:华中理工大学出版社，1990.

［3］ 熊合金，徐华中.灰色控制［M］.北京:国防工业出版社，2005:9.

［4］ 解 伟.灰色预测和灰色关联度在结构可靠度中的应用［J］.华北水利水电学院学报，2005(6):20-25.

［5］ 刘法贵.灰色数学及其应用［M］.开封:河南大学出版社，2002:21-88.