应用 GM(1，1)模型预测城市中长期用水量

王 伟 廖正福

用水量预测是城市在进行水工程规划时的一项重要任务，关系着城市水资源的长远规划与管理。城市用水量由于受居民生活、工业产值、水的重复利用率、节水技术以及用水价格等多种因素的影响，变化比较复杂，表现为随机波动性大，缺乏规律性，这给城市未来用水量预测带来了极大的困难，传统的指标预测法已很难做出准确的预测。本文应用灰色GM(1，1)模型对城市用水量进行预测，避免了讨论城市用水系统内部以及外部的各种复杂因素对用水量的影响，而只需要对已知的城市用水量序列进行分析，从中挖掘有价值的信息，对离散的用水量数据建立微分方程的动态模型，从而进一步获得变量的时间响应函数［1］，实现对城市未来用水量的合理预测和有效控制，为城市未来规划用水量的准确确定提供了一种切实可行的有效方法。

1 灰色GM(1，1)模型的建立

灰色预测具有要求原始数据少(不少于4个即可)、不考虑分布规律、不考虑变化趋势、运算方便、易于检验等优点［2］，因此得到了广泛的应用。其中GM(1，1)模型是最常用的一种灰色预测模型，它是由一个只包含单变量的一阶微分方程构成的模型［3］，是作为需水量预测的一种有效模型，建立GM(1，1)模型只需要一个历史用水量序列q(0)，建立过程及求解方法如下:

1)设历史用水量数列为:

2)可行性检验。对给定的历史用水量序列 q(0)建立灰色GM(1，1)模型的可行性进行判断，判断的准则为:用来建模的原始序列q(0)的级比σ(0)(k)，如果满足那么可以认为原始序列q(0)可以用来建立GM(1，1)预测模型。其中级比σ(0)(k)的计算公式为:

3)对历史用水量数列q(0)进行一次累加(1-AGO)生成一次累加数列:

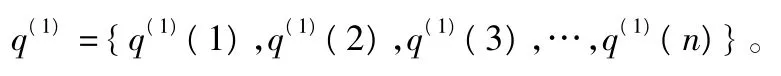
4)对一次累加数列q(1)建立以下形式的一阶微分方程:

其中，

6)式(1)是关于变量q的一阶微分方程模型，其解即为一次累加数列q(1)的预测值:

再经一次累减逆运算就可以得到原始数列q(0)的预测值:

式(2)，式(3)就是灰色GM(1，1)模型的时间响应函数，也就是灰色模型GM(1，1)预测序列的计算公式。

2 模型精度检验

通常采用后验差方法对灰色模型的预测精度进行检验，后验差检验是基于实际值与模型预测值之间的统计情况进行检验的一种方法，它是以残差为基础，根据各期残差绝对值的大小，考察残差较小的点出现的概率以及与预测误差方差有关指标的大小［3］。其检验的具体步骤和评价方法分别介绍如下。

2.1 后验差检验步骤

设历史用水量序列为:q(0)={q(0)(1)，q(0)(2)，q(0)(3)，…，q(0)(n)}。其预测值序列为:∧q={∧q(0)(1)，∧q(0)(2)，∧q(0)(3)，…，∧q(0)(n)}。

记k时刻的残差为:e(k)=q(0)(k)－∧q(0)(k)，k=1，2，3，…，n。

分别求出历史用水量序列q(0)，残差e(k)的平均值:

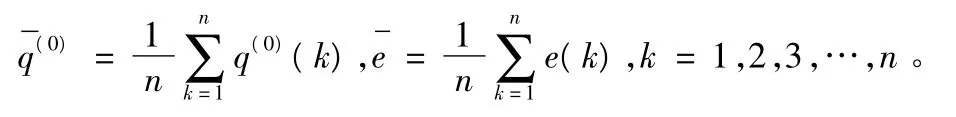
2，3，…，n。最后求出后验差检验的两个重要的数据，即后验差比值C，小误差概率P:

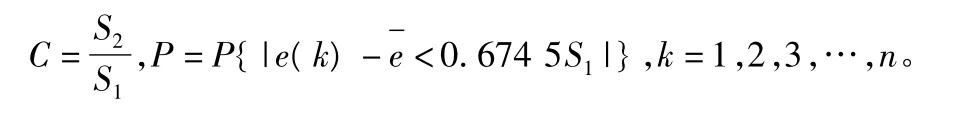
2.2 后验差检验评价方法

按C和P两个指标可以综合评定预测模型的精度，预测精度等级如表1所示。指标C越小越好，C越小表明尽管历史数据很离散，但是模型所得的预测值与实际值之差并不太离散;指标P也是越大越好，P越大表明残差与残差平均值之差小于0.674 5S1给定值的点较多，也就是说预测误差较小的概率大，预测精度高。

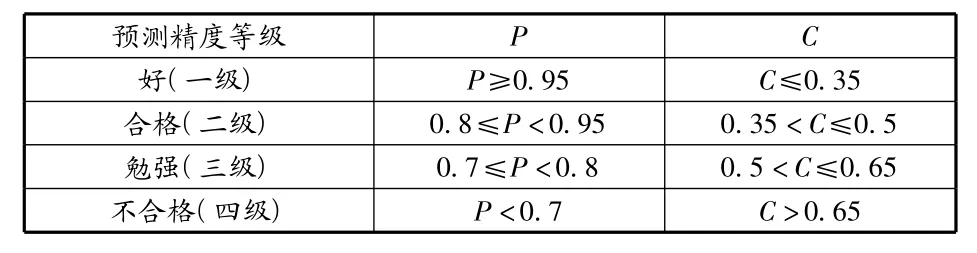
表1 预测模型精度等级表

3 应用实例

表2是某市2000年～2007年的历年用水量数据，以此数据作为该市用水量的原始序列，依据上述阐述的灰色系统建模理论建立 GM(1，1)模型。

原始数据系列为:

经可行性检验知，原始数据序列可以用来建立GM(1，1)模型。利用 Matlab［4］软件计算得到的模型参数为:a= －0.018 7，u=0.371 7，所建立的灰色GM(1，1)模型的预测序列的计算式为:

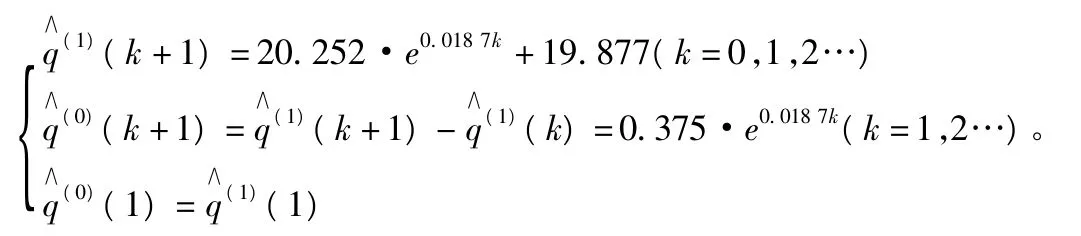
利用上式对该市2000年～2007年用水量进行计算，实际用水量的值与模型拟合值列于表3。

表2 某市2000年～2007年总用水量统计表

表3 实际用水量值和模型拟合值对比表

对上述模型进行后验差检验，其结果为:C=0.32＜0.35，P=1。查预测模型精度等级表知，模型等级为一级，故可以用此模型对该市未来的工业用水量做出预测。利用上述模型对该市2015年和2020年的用水量作出预测，预测值分别为0.496 4亿 t、0.548 7 亿 t。

4 结语

本文根据灰色系统理论，建立了灰色GM(1，1)模型，并将其应用到某市的用水量预测中，经检验，模型的预测精度都达到了97%以上，模型的预测拟合结果令人满意，预测结果更加符合当地的实际情况，对该市未来水资源的规划管理具有重要的指导意义。

［1］ 邓聚龙.灰理论基础［M］.武汉:华中科技大学出版社，2002.

［2］ 张雅君，刘全胜.需水量预测方法的评析与择优［J］.中国给水排水，2001，17(7):27-29.

［3］ 邓聚龙.灰色预测与决策［M］.武汉:华中理工学院出版社，1985.

［4］ 何仁斌.MATLAB 6工程计算及应用［Z］.2001.