潜水器结构可靠性计算的自适应β球方法＊

马永亮 曲先强 崔洪斌 石德新

（哈尔滨工程大学多体船技术国防重点学科实验室 哈尔滨 150001）

在结构可靠性分析中最重要的内容是求解结构的失效概率.一般来说，除了简单的极限状态函数外，结构失效概率的计算都比较困难.寻求高效、精确的计算方法是结构可靠性研究的一个重要内容.Monte Carlo方法具有模拟的收敛速度与随机变量的个数无关，极限状态函数的复杂程度与模拟过程无关的优点［1－2］，是一种应用广泛的数值计算方法.直接 Monte Carlo法（crude monte carlo method）的误差与无偏统计量的方差成正比，与模拟次数的平方根成反比.所以需要采用缩减方差抽样方法来提高计算效率［1－4］.Harbitz提出了一种特殊的Monte Carlo法，称为β球法［5－6］.β球法在安全域剔除了一个球形或超球形的抽样区域，特别适用于极限状态函数为凸曲面的情况.孙海虹［7］、张晓军［8］、吴亚舸［9］采用β球法进行了结构可靠性研究.虽然β球法得到了广泛的应用，但这种方法一般需要在求解之前给出β球的半径.所以，这种方法不能独立使用.基于这一点本文根据β球法自身求解特点提出了一种自适应抽样算法来确定初始β球的大小，使β球法不再依赖于其他方法，并将此方法应用于潜水器耐压圆柱壳结构可靠性分析中.

1 一般β球方法

1.1 一般β球方法的基本原理

β球方法必须满足以下的假设：（1）基本随机变量服从正态分布；（2）可靠性指标β的估计值必须事先知道.

β球将空间分为了2个部分｜X｜≤β和｜X｜＞β，其中｜X｜≤β为中心在原点的m维超球体.根据全概率公式，失效概率Pf可以表示为

式中：χm为自由度为m的χ2分布函数.

失效概率Pf的一个无偏估计表示为

式中：k为样本的大小；I［G（Yi）］为示性函数，在安全域I＝0，在失效域I＝1；Yi为标准正态空间的一组随机变量.

1.2 β球方法抽样策略

基本随机向量X抽样可以表示为

式中：Ri为Xij的模，有；αij为随机方向矢量，满足

由于Ri和αij之间是相互独立的，所以可以对Ri和αij分别进行抽样，具体的抽样方法见文献［5，6，10］.

1.3 样本变换及其改进

从式（2）可以看出，失效概率的求解只与示性函数有关.只要求解出示性函数的结果就可以了.所以可以将相互独立的标准正态分布样本变换为原来的分布，再代入原来的极限状态方程求解示性函数.这种变换方法是一般变换方法的逆变换.

1.3.1 一般变换方法

任意相关随机变量必须经过2步转化才能变成独立标准正态分布.第一步是将相关非正态随机变量转化为相关正态随机变量；第二步是将相关正态随机变量转化为独立正态随机变量.

将非正态随机变量转化为正态随机变量最常用的方法是当量正态化方法和映射变换方法.通过当量正态化方法进行变换后的相关系数可以根据NATAF变换得到［11］.变换后的相关系数表示为

式中系数F已经由Liu给出［12］.

相关正态随机变量转化为独立的标准随机变量可以采用Choleshy分解方法进行.通过这些方法就可以将任意相关随机变量转化为独立的标准正态分布的随机变量.变换流程图见图1.上述方法的逆变换也是成立的.文中将上述方法的逆变换用于结构可靠性分析的β球方法中.

图1 变换过程

1.3.2 逆变换的验证

有2个随机变量R和S，R服从正态分布，S服从极值I型分布，相关系数为ρRS＝0.5，其中μR＝100，μS＝50，δR＝0.12，δS＝0.15.采用 Monte－Carlo方法，使用标准正态分布的随机数经过逆变换来得到R和S的分布以及相关系数.样本数为40 000时的模拟结果见图2和图3.模拟得到的相关系数为0.491 3.可以看出本文采用的逆变换是准确可靠的.

图2 随机变量R的模拟结果

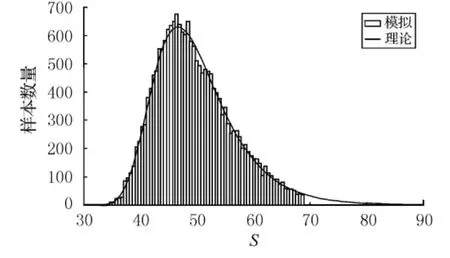
图3 随机变量S的模拟结果

1.4 扩展的一般β球方法的计算过程

扩展的一般β球方法的计算流程图见图4.图4中Yi为标准正态空间的一组随机变量；Xi为一组非正态分布随机变量；G（X）为极限状态方程.

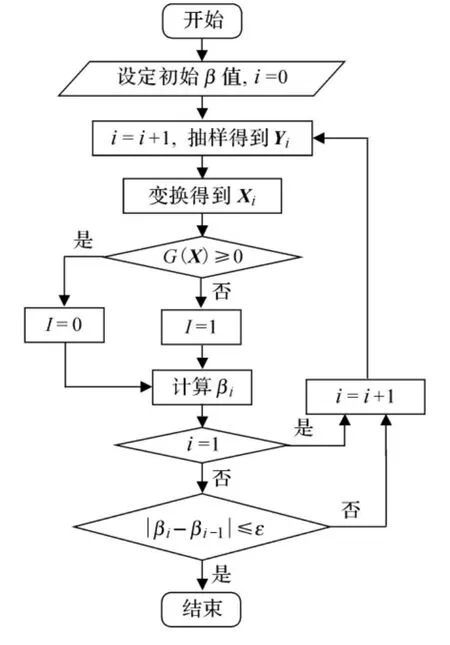
图4 扩展的一般β球方法计算流程图

2 自适应抽样算法的提出

β球方法的使用过程中需要对各随机变量进行抽样，根据抽样计算结构的失效概率.可以利用抽样结果估算结构可靠性指标，以这个估算的可靠性指标作为初始β球的大小，然后再根据扩展的一般β球方法求解结构的失效概率.

2.1 自适应抽样算法

以包含两个标准正态分布随机变量的极限状态方程为例进行说明所提出的自适应抽样算法，对于不服从正态分布的情况按照1.3节的变换方法变换为标准正态分布.算法的原理如图5所示.具体的步骤描述为［13］：

步骤1假设抽样范围为β0和β1之间，β0取得相对较小一点，β1取得相对较大一点.

步骤2抽取样本，并代入极限状态方程中判断极限状态方程G（X）是否小于0，如果小于0，计为P1，停止抽样.

步骤3求取P1点处的方向余弦，P1点的方向余弦和P2点的方向余弦相等，进行变换，根据极限状态方程采用二分法求解出β2.

步骤4以β0和β2为抽样区间重复步骤2，步骤3，在P2点根据重要抽样策略进行抽样，求出β3.

步骤5重复步骤2～4，3～5次就可以得到合适的β值.

图5 自适应抽样算法原理示意图

2.2 自适应抽样算法的验证

2.2.1 独立标准正态分布

以文献［14］中的一个例题为例进行可靠性指标的估算.已知非线性极限状态方程0.1（x1－式中：x1，x2都服从标准正态分布.假设β在1和6之间，经过5次计算，得到的结果见图6.由图6可见两者十分接近.为了进一步验证计算结果，极限状态函数和抽样区域见图7.

2.2.2 独立非标准正态分布

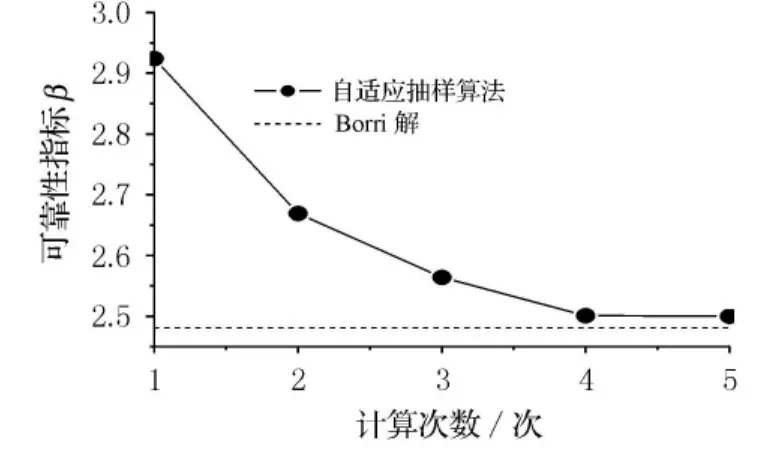
图6 正态分布的估算结果

图7 计算结果的比较

以文献［4］中的一个例题为例进行可靠性指标的估算.已知非线性极限状态方程567fr－0.5H2＝0.f服从正态分布，μf＝0.6，δf＝0.131；r服从正态分布，μr＝2.18，δr＝0.03；H服从对数正态分布，μH＝32.8，δH＝0.03.假设β在1～6之间，经过6次计算，得到的结果如图8所示.图中虚线为验算点法的解，可以看出两者十分接近.

图8 非正态分布的估算结果

2.2.3 相关非正态分布

以文献［4］中的一个例题为例进行可靠性指标的估算.已知极限状态方程为X1X2－130＝0.X1服从对数正态分布，μX1＝38.0，δX1＝0.1；X2服从正态分布，μX2＝7.0，δX2＝0.15；相关系数ρX1X2＝0.5.假设β在1和6之间，经过6次计算，得到的结果和验算点法的比较见图9.

3 自适应β球方法的提出

3.1 自适应β球方法

图9 相关非正态分布的估算结果

对于一个含有任意个非正态分布随机变量的极限状态方程，首先采用自适应抽样算法估算出初始β球的大小，再根据扩展的一般β球方法来计算结构的可靠性指标.

3.2 计算实例

我国现行的《潜水系统和潜水器入级与建造规范》，给出了耐压环肋圆柱壳结构的5种校核公式.大量的潜水器结构可靠性研究文献将这5种校核公式作为失效模式的极限状态方程.具体说明以及随机变量的分布和特征参数见文献［10］.对于潜水器这样安全要求比较高的结构，一般认为只要有一个失效模式出现就认为整个结构失效，所以潜水器结构系统可靠性是一个串联模式的可靠性问题.

3.2.1 单个失效模式的可靠性计算

采用提出的自适应β球方法对五种失效模式的可靠性分别进行了计算，全部的计算结果见表1，其中G3的计算结果和验算点法的比较见图10.

表1 计算结果

图10 G3的计算结果

3.2.2 系统可靠性计算

采用自适应抽样算法计算每一个失效模式的可靠性指标βi（i＝1，2，3，4，5），然后取min（βi）作为β球的大小，采用扩展的一般β球法进行计算，示性函数I［g（X）］表达为

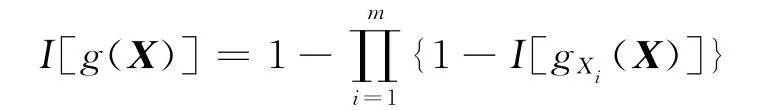
式中：I［gXi（X）］为第i个失效状态的示性函数.系统可靠性的计算结果如图11所示.

图11 系统可靠性计算结果

将本文的计算结果和重要样本法（important sample method）、PCM 法［15］以及 Drezner积分方法（Drezner integral method）［16］的结果进行了比较.结果表明本文的计算结果和Drezner积分方法以及PCM法接近.Drezner积分方法是一种特殊的Gauss－Hermite求积法，在理论上只存在积分误差.PCM方法的计算结果比本文方法略小，文献［17］指出PCM方法在计算串联结构系统可靠性时往往给出较保守的计算结果，这和本文的计算结果基本一致.本文方法和重要样本法有一定的差异，这主要是因为重要样本法收敛较慢，在相同的样本大小（sample size）下，本文方法已收敛，而重要样本法还没有收敛.这主要归功于自适应抽样算法提供了一个合理的初始β球尺寸.

4 结束语

Harbitz提出的β球法是一种应用广泛且高效的数值计算方法，但这种方法不能独立使用.针对这一点，本文提出了一种自适应抽样算法.这种算法可以根据β球方法的抽样特点估计出β球的大小，算法的效率较高，经过5～6步的迭代就可以得出和验算点法相近的计算结果.包含自适应抽样算法的自适应β球方法收敛速度高于重要样本法，且计算准确性较高.这种自适应β球方法特别适用于极限状态函数是凸曲面以及结构系统可靠性的模拟，对一般的极限状态方程也是有效的.

本文最后使用提出的方法计算了潜水器耐压圆柱壳结构各个失效模式的可靠性和系统可靠性，并和验算点法、重要抽样法、PCM方法以及Drezner积分方法进行了比较，验证了本文提出的方法的计算效率和准确性.

［1］贡金鑫.工程结构可靠度计算方法［M］.大连：大连理工大学出版社，2003.

［2］肖 刚，李天柁.系统可靠性分析中的蒙特卡罗方法［M］.北京：科学出版社，2003.

［3］谢祚水，王自力，吴剑国.潜艇结构分析［M］.武汉：华中科技大学出版社，2002.

［4］赵国藩，金伟良，贡金鑫.结构可靠度理论［M］.北京：中国建筑工业出版社，2000.

［5］Harbitz A.An efficient sampling method for probability of failure calculation［J］.Structural Safety，1986（3）：109－115.

［6］余建星，郭振邦，徐 慧，等.船舶与海洋结构物可靠性原理［M］.天津：天津大学出版社，2001.

［7］孙海虹.结构可靠性分析改进的重要抽样法［J］.武汉交通科技大学学报，1994，18（3）：241－246.

［8］张晓军，常新龙，杨 青.利用改进的Monte Carlo β球法计算结构可靠性［J］.强度与环境，2005，32（2）：52－56.

［9］吴亚舸，吴剑国.潜艇耐压圆柱壳结构可靠性的数值模拟计算法［J］.造船技术，2002（1）：15－18.

［10］马永亮.考虑腐蚀影响的潜艇结构可靠性研究［D］.哈尔滨：哈尔滨工程大学船舶工程学院，2009.

［11］Melchers R E.Structural reliability analysis and prediction（Second Edition）［M］.New York：John Wiley ＆Sons Ltd.，1999.

［12］Liu Peilin，Kiureghian A D.Multivariate distribution models with prescribed marginals and covariances［J］，Prob.Engineering Mechanics，1986（2）：105－112.

［13］Nie Jinsuo.A new directional method to assess structural system reliability in the context of performance－based design［D］.Baltimore：Johns Hopkins University，2003.

［14］Borri A，Speranzini E.Structural reliability analysis using a standard deterministic finite element code［J］.Structural Safety，1997，19（4）：361－82.

［15］Pandey M D.An effective approximation to evaluate multi－normal integrals［J］.Structural Safety，1998，20：51－67.

［16］Drezner Z.Computation of the multivariate normal integral［J］.ACM Transactions on Mathematical Software，1992，18（4）：470－480.

［17］Mori Y，Kato T.Multi－normal integrals by importance sampling for series system reliability［J］.Structural Safety，2003（25）：363－378.