考虑路段失效的军事物流配送中心选址模型＊

李 东 晏湘涛 匡兴华

（国防科技大学信息系统与管理学院1） 长沙 410073） （国防科技大学人文与社会科学学院2） 长沙 410074）

军事物流配送中心（military logistics distribution center，MLDC）是战场保障网络的支撑点，对战场物流的流量、时间、成本有重大影响.由于战场保障网络是后勤保障的重心，因此物流通道在战时常常遭到敌人的打击.从战争实际来发，MLDC位置的选择需要考虑物流通道失效的情况［1］.

考虑失效的设施选址，称为可靠（的）设施选址（reliable facility location）.可靠设施选址，就是前摄地选择设施位置，使配送系统不但在正常情况下能够实现最优化，而且在发生失效时仍能运行“良好”［2］.Daskin研究团队以无容量限制选址问题（uncapacitated facilities location problem）为基础，采用不同的选址目标系统地研究了设施无容量限制情况下的可靠选址问题［3－4］；Dinakar扩展了Daskin团队的研究，研究了设施存在能力限制的可靠选址问题，要求设施能力同时满足无失效时的基本指派和发生失效后再指派的需要［5］；O＇Hanley和 Church［6－7］在研究覆盖型网络的可靠设施选址问题时，考虑了覆盖路径对选址决策的影响.以上学者的研究都是假设物流网络中的设施存在失效可能.然而，对于战场保障网络而言，物流通道比保障设施更容量出现失效.因此，本文在研究战场保障网络的军事物流配送中心可靠选址问题时，把失效的焦点集中在配送路段上，突出路段失效对选址决策的影响，采用最大覆盖模型进行研究.

1 问题描述

对于一个由部队用户、备选地址点、配送路段构成的战场保障网络，基本假设如下：（1）不考虑军事物流配送中心的供应能力；（2）每个路段都存在失效的可能，但只有一条路段失效；（3）能够建立的军事物流配送中心数目已知.军事物流配送中心的供应能力主要由战役级保障设施的保障效果决定.由于本文研究的重点是军事物流配送中心到部队用户之间的后勤保障，因此军事物流配送中心的供应能力不是本文考虑的内容，假设（1）成立.假设（2）是对未来战场环境的描述.假设（2）既能考虑到己方决策部门设计配送方案时的谨慎态度，又可以兼顾敌人企图通过打击补给线干扰对方战争行动的可能性.假设（3）是简化问题的必要假设.

考虑路段失效的军事物流配送中心选址问题，就是从给定的备选地址中选择出一个地址组合，使得由处于这些地址的军事物流配送中心构成的保障系统，无论是在无路段失效还是在出现路段失效的情况下，都能在满足覆盖半径的约束内覆盖尽可能多的需求量.

2 选址模型

定义以下符号.

I为部队用户集合，用i遍历；J为备选地址点集合，用j遍历；N为全部节点集合，N＝I＋J，且｜I｜＋｜J｜＝n；r为待建 MLDC数目；wi为部队用户i的需求；L为网络内全部路段集合；m为路段的数目；θ为权重系数.

式中：

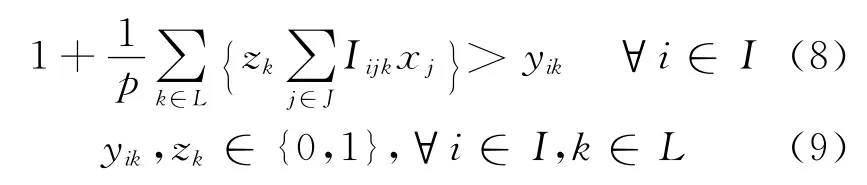
M1是一个双层规划.上层规划目标是要找到一个地址组合，使得由该地址组合构成的战场保障网络在无路段失效和出现路段失效时系统覆盖尽可能多的需求量，即目标函数（1）.目标函数（1）的第一部分表示无路段失效时战场保障网络覆盖的需求量，第二部分表示由某种地址组合x组成的战场保障网络在某一路段失效时覆盖的需求量H（x），H（x）由下层规划的目标函数（5）来决定.下层规划是目标是找到一个路段，使得该路段失效时系统覆盖的需求量最小.约束条件（2）是限定部队用户只能被开设的MLDC覆盖；约束条件（3）限定了待建MLDC的数量；约束条件（6）计算路段失效时系统覆盖的需求量.约束条件（7）和（8）把上下2层规划连接起来，约束条件（7）限定当路段k失效时，部队用户只能被开设的MLDC覆盖，在xj和yik之间建立联系，约束条件（8）限定在路径k失效的情况下，当且仅当覆盖部队用户i的MLDC数量大于0时，yik才能取值为1，在zk和xj之间建立联系.约束条件（4）和（9）是对决策变量xj，yi，yik，zk的0或1整数约束.

3 模型求解

3.1 下层规划的求解

为了下文表述方便，称下层规划为“最佳路段失效问题”.求解最佳路段失效问题的基本思想：首先，找出网络内供应点与需求点之间满足覆盖半径约束的可用覆盖路径；其次，任选一条路段使其失效，并对可用覆盖路径进行剪裁，得到此路段失效时网络节点之间的可达矩阵；然后，利用可达矩阵和部队用户的需求量计算网络的覆盖程度；最后，比较不同路段失效时网络覆盖程度的大小，找出使网络覆盖程度最小的路段.

对于网络G，有n个顶点，建立可达矩阵

元素apq的取值为0或1.当取值为1时，表示节点p到节点q的路径距离满足覆盖半径约束；当取值为0时，节点p到节点q的路径距离不满足覆盖半径约束.

根据最大覆盖设施选址问题中关于覆盖的定义，有如下命题成立.

命题1当网络中路段ek的长度大于覆盖半径时，对于网络内任意2个节点p和q，删除路段ek不会影响p与q之间的覆盖状态.

证明如果p与q之间的最短路径包括了路段ek，p与q之间的距离肯定大于覆盖半径，因此若欲p覆盖q，那么p与q之间的最短路径一定不能包括路段ek.由此可知，删掉路段ek不会影响整个网络的覆盖程度.

对于由部队用户集合I和备选地址点集合J以及I与J之间的路段构成的网络G，最佳路段失效问题的具体求解步骤.

步骤1删除无影响路段.根据设施覆盖半径的长度，移除G中长度大于覆盖半径的路段.

步骤2搜索某个给定选址方案的可用覆盖路径.若在节点p建立MLDC，那么根据点p的覆盖半径约束，找出从点p出发符合要求的路段，然后根据这些路段的尾节点继续搜索，直到找出所有符合覆盖半径约束的路径，得到全部设施的可用覆盖路径集P.

步骤3根据P建立初始可达矩阵An×n（A内元素的初始值为0）.只要点q处的部队用户包含于点p处的MLDC发出的某条可用覆盖路径之内，那么apq，apq＝1；否则，apq，apq＝0.

步骤4从全部路段集中任选一个路段ek，令路段ek失效（即路段ek的长度为∞），并使路径集P中包含路段ek的可用覆盖路径，去掉自路段ek以后的部分，得到新的可用覆盖路径集Pk.

步骤5根据Pk建立路段ek失效情况下的可达矩阵（Ak内元素的初值为0）.路段ek失效时，Ak中的元素由Pk中的可行覆盖路径决定.只要点q处的部队用户包含于点p处的MLDC发出的某条可用覆盖路径之内，那么＝1；否则＝0.

步骤6计算路段ek失效时网络覆盖程度的变化量Ck.记G的需求矩阵为D＝｛d1，d2，…，dn｝，若点q处为部队用户，那么dq＝wq，若点q处为备选地址点，那么dq＝0，Ck的值由下式求得.

步骤7选择其他路段，重复步骤4～6.当每条路径都失效过一次之后，停止循环.

步骤8确定最优解.使Ck最大的路段ek即为最佳路段失效问题的最优解.

其中，在步骤2求解可用覆盖路径中，由于每条可用覆盖路径最多遍历每个节点一次，所以路径的边数不会超过（n－1）.将每条路径每次推进一步，使得搜索可以在（n－2）内完成.

3.2 基于遗传算法的模型求解

遗传算法（genetic algorithm，GA）是一种全局优化搜索算法，具有简单通用、鲁棒性强、适于并行处理以及应用范围广等显著特点［8］.本文采用遗传算法对模型进行求解，通过选择、交叉、变异操作识别出好的染色体，求得最佳选址地点.

基于遗传算法的模型求解具体步骤如下.

步骤1初始化算法的相关参数，产生初始种群.相关参数主要包括：种群规模K、进化代数G、选择规模系数pselect、交叉概率pcross等，并令进化次数a＝0.

步骤2按照目标函数（1）计算初始种群中各条染色体的适应度.

步骤3根据染色体适应度的大小，在种群中选择部分染色体.

步骤4对选择的染色体进行交叉操作，得到子代染色体.

步骤5对子代染色体进行变异操作，计算变异后子代染色体的适应度.

步骤6根据子代后染色体的适应度的大小，把变异的子代染色体插入父代种群中，得到新的种群.

步骤7重复步骤2～6，直到进化次数达到进化代数G停止.

步骤8确定进化代数G内具有最大适应度的染色体，该染色体所对应选址方案，即为模型的最优解.

4 应用算例

在某次战区演习的进攻战斗中，后勤部门决定在某机械化师的作战地域内建立3个军事物流配送中心，为该师的10个营级战斗分队提供物资保障.经初步考察已有5个地点被列为备选地址，备选地址与战斗分队构成的物流网络如图1所示.后勤部门确定军事物流配送中心的覆盖半径为2，各战斗分队的需求量、网络中各节点之间的距离已知并在图中表示出来.图中点1～10为需求点，即战斗分队的位置，点A～E为备选地址点.

图1 算例网络图

令式（1）中θ的取值为0.7，种群规模K＝40，进化代数G＝400，选择规模系数pselect＝0.9，交叉概率pcross＝0.7.采用 Matlab7.0编程求解，求解结果如表1所列，算法进化过程如图2所示.

表1 模型结果比较

图2 算法进化过程

由表1可知，本文模型的选址结果与不考虑路段失效情况的最大覆盖选址结果存在差异.在无路段失效时，M0的选址方案能够覆盖最多的需求量，选址结果优于M1.然而，在最佳路段失效情况下，M0的选址方案不再是最优的，M1的选址方案能够在最佳路径失效时损失较低的需求覆盖量.特别地，M1的选址方案在无路段失效时覆盖的需求量方面与M0的选址方案相差不多，还能够有效控制最佳路段失效时的系统损失.

对于后勤部门来说，可以根据战斗分队作战地域的资源状况情况结合模型的特点，选择适当的模型进行军事物流配送中心选址决策.当作战地域内交通便利，保障资源丰富时，可以采用M0进行选址决策.丰富的保障资源可以使后勤部门在最佳路段失效做出快速反应，迅速地就地筹措物资，并通过便利的交通通道把用户急需的军事物资及时送达指定地点，弥补M0的选址方案在最佳路段失效时的不足.当作战地域远离战役后方、交通不便、保障资源稀少、自然资源匮乏、军事物资难以就地筹措时，战场物资保障完全依靠前出保障时，可以采用M1进行选址决策.M1选址方案可以获得较高的需求覆盖量，又能控制路段失效时的系统损失，能够降低紧急情况下应急保障对就地筹措保障方式的依赖程度.

5 结束语

本文研究了战场保障网络设计中的军事物流配送中心选址问题，考虑了配送路段失效的情况，以最大化系统在无路段失效时和最佳路段失效时所覆盖的总需求量作为优化目标，建立了双层规划形式的选址模型.未来对于保障设施选址问题的研究可以考虑从以下几个方面着手：（1）多路段失效情况下的设施选址.从战争实际来看，路段失效的个数取决于战争双方的实力，呈现出一定的不确定性.因此为了更接近实际，需要对本文模型进行路段随机失效情况下的扩展；（2）结合用户敏捷性要求的选址.战时物资保障是供需双方共同作用的结果，供方具有配送能力约束，需方会有保障的时效性要求.因此，建立满足用户敏捷性要求选址模型，是一个值得深入研究的问题；（3）针对大型问题的模型求解算法.

［1］晏湘涛，李 东，匡兴华.基于共识度决策的军事物流配送中心选址研究［J］.武汉理工大学学报：交通科学与工程版，2010，34（1）：27－30.

［2］Snyder L V，Daskin M S.Models for reliable supply chain network design［R］.Evanston：Northwestern University，2006.

［3］Snyder L V.Planning for disruptions in supply chain networks［M］.New Orleans：INFORMS，2005.

［4］Snyder L V，Daskin M S.Reliability models for facility location：the expected failure cost case［J］.Transportation Science，2005，39（3）：400－416.

［5］Dinakar G.Capacitated facilities location problems with unreliable facilities［D］.Fayetteville：University of Arkansas，2005.

［6］O＇Hanley J R，Church R L.Designing robust cover－age networks to hedge against worst－case facility losses［J］.European Journal of Operational Research，2010，In Press.

［7］Church R L，ReVelle C S.The maximal covering location problem［J］.Papers of the Regional Science Association，1974，32：101－118.

［8］刑文训，谢金星.现代优化计算方法［M］.北京：清华大学出版社，2007.