基于粒子群优化算法下的灰色系统船闸货运量预测＊

杨 星 王娅娜

（江苏省水利科学研究院 南京 210017）1） （河海大学交通与海洋学院 南京 210098）2）

0 引 言

航道货运量预测是制定有关政策、编制运输发展规划和运输企业经营决策、日常管理的依据［1］，也是进行航运规划，确定各枢纽的通航建筑物规模最直接和最重要的基础性工作.目前常用的某些预测方法（回归分析、神经网络法［2－5］、移动平均法、指数平滑法等），若样本较小，常造成较大误差 ，使预测目标失效.若样本较大，则计算复杂，不易应用.灰色系统理论是研究解决灰色系统分析、建模、预测、决策和控制的理论.灰色预测的模型所需建模信息少，运算方便，建模的精度高，在各种预测领域都有着广泛的应用［6－7］.近年来，在交通流量的预测中，应用灰色理论获得了较好的效果［8］.但在内河运量的预测却是从2000年开始才陆续有学者进行研究［9－10］，这些研究主要集中在中短期预测领域，对于长期预测尚有待于时间的检验和进一步的探讨论证.

本文通过粒子优化算法可以避免矩阵运算，降低运算难度.文章最后通过与实测结果的对比分析与验证，分析研究基于粒子优化算法灰色系统模型预测船闸货运量时的精度，并比较了基于粒子优化算法和基于最小二乘法灰色系统预测法的预测精度.

1 基于粒子群优化算法下的灰色预测模型GM （1，1）的建立

1.1 模型的建立

GM（1，1）表示一阶的、具有两个参数变量（a，b）的微分方程模型，具体形式如下.

设有数列x（0）共有n个观测值，表示为

对x（0）做一阶累加，生成新的序列x（1）

令z（1）为x（1）的均值序列

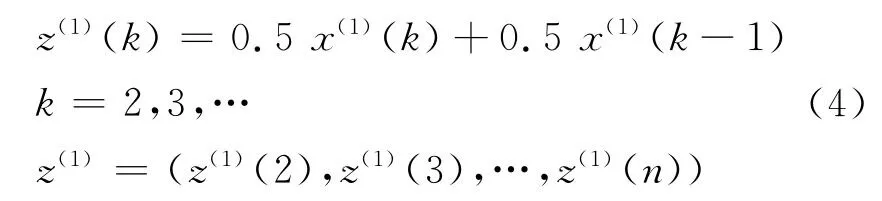
则GM（1，1）的灰微分方程模型为

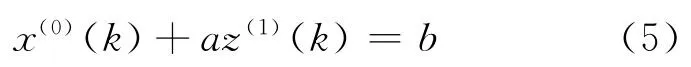
以k＝2，3，…，n代入式（5），有

对上述离散方程组，用随机粒子群优化算法求解，可得P＝（a，b）T.把所求得的系数P＝（a，b）T代入到式（5），然后求解微分方程，得到GM（1，1）预测模型为

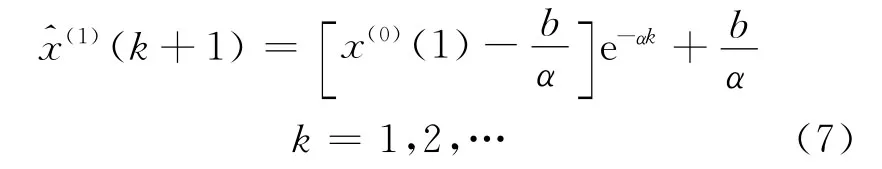
以上所述的即是GM（1，1）的建模过程，也是建立船闸货运量灰色预测模型的基础.

1.2 粒子群优化算法（PSO）

粒子群优化算法由Kennedy和Eberhart在1995年提出，该算法模拟鸟集群飞行觅食的行为.设想一群鸟在随机搜寻食物，这个区域里只有一块食物，所有的鸟都不知道食物在哪里，但他们知道目前距离食物还有多远，那么找到食物的最简单的方法就是找寻距离食物最近的鸟的周围区域，及根据自身飞行经验判断食物的所在.每个寻优的问题解都被想像成一只鸟或者称为粒子.所有的粒子都有一个目标函数以判断该粒子目前位置的好坏，每一个粒子必须具有记忆性，能记得所搜寻到的最佳位置.每一個粒子还有一个速度以决定飞行的距离和方向.

粒子群优化算法流程如下：（1）初始化.将族群做初始化，以随机的方式求出每一个粒子（鸟）的初始位置与速度；（2）评估.依据目标函数计算出其目标值以作为判断每一个粒子所处位置的好坏；（3）查找个体极值.找出每一个粒子到目前为止搜寻过程中的最佳解，这个最佳解称为个体极值；（4）查找全局极值.找出所有粒子到目前为止所搜寻到的整体最佳解，这个最佳解称为全局极值；（5）更新粒子速度和位置.假设搜索空间为D维，粒子群中第i个粒子的2个状态量——位置和速度分别用xi＝（xi1，xi2，…，xiD）和vi＝（vi1，vi2，…，viD）表示，该粒子迄今为止搜索到的最好位置（即历史最优值）记为pi＝（pi1，pi2，…，piD），所有粒子迄今为止搜索到的最好位置记为pg＝（pg1，pg2，…，pgD）.那么该粒子的速度和位置更新等式（第d维）可表示为

式中：Vid为每一个粒子在第d维的速度；i为粒子的编号，粒子数一般取50，对于比较难的问题或者特定类别的问题，粒子数可以取超过100的数；d为维度；ω为惯性权重，常数，用来控制粒子的历史速度对当前速度的影响程度，一个较大的ω值能加速粒子搜索新的区域，因此，选取适当的ω值能平衡PSO算法的全局和局部搜索能力，从而得到更好的解.本文取为0.8；c1，c2为学习常数，本文取2；rand（）表示在范围［0，1］内取值的随机函数；Pid为每一个粒子到目前为止，所出现的最佳位置；Pgd为所有粒子到目前为止，所出现的最佳位置；Vmax和Vmin是常数，决定粒子在一个循环中最大的速度，人为设定.式（8）中第1部分为粒子先前的速度，它使粒子有在搜索空间中扩张的趋势，从而使算法具有全局搜索的能力；第2部分为“认知”部分，表示粒子吸取自身经验知识的过程；第3部分为“社会”部分，表示粒子学习其他粒子经验的过程，表现了粒子间信息的共享与社会协作.

1.3 粒子群优化算法求解灰色系统预测模型参数变量a，b

参照式（6），取船闸货运量问题的目标函数为

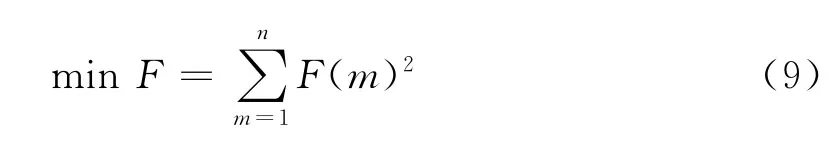
式中：F表示为

具体计算步骤如下.

1）初始化粒子群 由于式（9）中只存在2个变量（a，b），搜索空间为2维.取粒子数＝50，c1＝2，c2＝2，ω＝0.8，最大迭代数＝1 000.

2）假设a的取值范围为［a1，a2］，b的取值范围为［b1，b2］，则第一维和第二维50个粒子初始位置可以分别设置为

式中：a和b的取值范围可以先取大，先在一个较大的范围内进行搜索，然后根据结果逐步缩小搜索范围，直到最优解满足要求为止.

3）第一维和第二维50个粒子的初始速度可以分别设置为

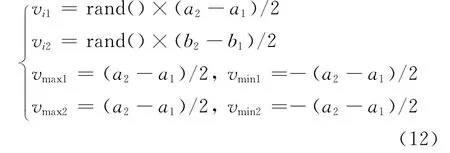
式中：vmax1和vmin1为第一维的速度最大和最小值；vmax2和vmin2为第二维的速度最大和最小值.

4）用目标函数评价所有粒子.

5）将初始评价值作为个体历史最优解Pid，并寻找群体内最优解Pgd.

重复执行以上步骤，直到满足终止条件或达到最大迭代次数，其中注意事项包括：（1）对每一个粒子，按式（8）计算［xi1，xi2］和［vi1，vi2］.当xid，vid超过其范围时，按边界取值；（2）用式（9）评价所有粒子，评价值为minF；（3）若某个粒子的当前评价值优于其历史最优评价值，则记当前评价值为该历史最优评价值，同时记当前位置为该粒子历史最优位置，更新Pid；（4）寻找当前群体内最优解，若优于历史最优解，则更新Pgd.

最终计算结果为

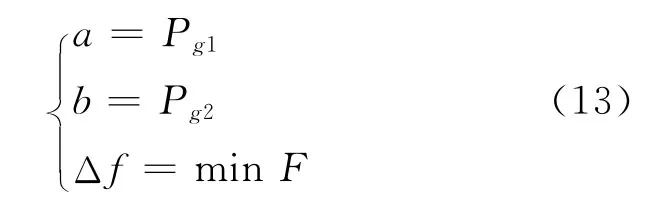
式中：Δf用于估计计算误差，数值越小时计算结果越优.

2 GM （1，1）模型船闸货运量预测

建模数据采用1996～2005年淮阴船闸的货物运输量（见表1），该数据为原始数据序列.

表1 淮阴船闸近年货物运输量 万t

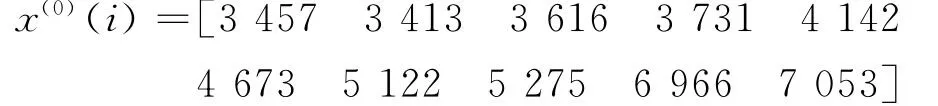
按照GM （1，1）建模机理，首先对x（0）做一次累加生成计算得（i＝1，2，3…）：

然后根据式（4）计算得（i＝2，3…）：

粒子群优化算法求解a＝－0.102 471 368 29，b＝2 552.303 797 468 35.另外，参照文献［15］中的最小二乘法计算得出a＝－0.101 513 575 46，b＝2 627.581 978 163 14.分别代入GM（1，1）模型，则船闸货运量预测模型为

累减还原得到

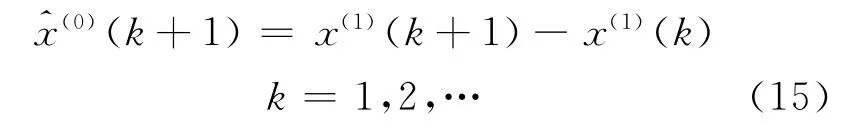
应用该模型对1996～2005年淮阴船闸货运量进行计算，并进行模型精度的比较（见表2）.比较结果粒子群优化法平均相对误差为3.81%，最小二乘法平均相对误差为3.79%，两者均小于10%，预测模型精度较好.

表2 1996～2005年淮阴船闸货运量模型预测值及误差值

最小二乘法需要求解矩阵（一般为奇异矩阵），其求解过程烦琐且不易获得近似解，所以本文进行了一些改进，用粒子群算法代替最小二乘法进行参数计算.两者求解数据的本质都一样，都是寻求经验公式并使其最大限度的拟合到观测数据，其结果也是相近的.最小二乘法出现较早，粒子群算法出现较晚.如果把最小二乘法看做是一种理论解，粒子群算法则更像是数值解，所以后者适应面更广，不需要烦琐的矩阵运算，所以算法上优于最小二乘法.

应用基于粒子群优化算法的灰色系统船闸货物运输量模型，进行远景预测（见表3）.

表3 2006～2010年淮阴船闸货物运输量预测值

3 结 论

1）相对于其他传统的预测方法，灰色GM（1，1）模型法由于具有所需数据少、计算量小的优点.

2）基于粒子优化算法建立的船闸货运量灰色预测模型，方法简便易行，结果合理可信，预测精度较高，在算法上优于基于最小二乘算法建立的船闸货运量灰色预测模型.

3）灰色预测法在中短期预测（n≤5）上具有优势，应用于船闸货运量的长期预测，尚有待于时间的检验和进一步的探讨论证.

［1］蒋惠园，杨大鸣.货运量预测方法的比较［J］.运筹与管理，2002，11 （3）：74－79.

［2］周伯荣，张丙伟.基于改进BP算法的中频淬火工艺参数预测［J］.江苏大学学报：自然科学版，2007，28（6）：495－499.

［3］郁 飞，罗春潮，许 勃.基于模糊神经网络的柴油机排气噪声预测［J］.华东船舶工业学院学报：自然科学版，2001，15（6）：54－57.

［4］Yin Hongbin，Wong S C，Xu Jianmin，et al.Urban traffic flow prediction using a fuzzy－neural approach［J］.Transportation Research Part C，2002（10）：85－98.

［5］Kalogqirou S A ，Pantelious S.Thermosiphon solar domestic water heating systems：long－term performance prediction using artificial neural networks［J］.Solar Energy，2000，69（2）：163－165.

［6］Wang M H，Hung C P.Novel grey model for the prediction of trend of dissolved gases in oil－filled power apparatus［J］.Electric Power Systems Research，2003，67（1）：53－58.

［7］Wang M H.Grey－extension method for incipient fault forecasting of oil－immersed power transformer［J］.Electric Power Components and Systems，2004，32（10）：959－975.

［8］Chen Shuyan，Qu Gaofeng，Wang Xinghe，et al.Traffic flow forecas ting based on grey neural network model［C］／／In：Proceedings of the Second International Conference on Machine Learning and Cybernetics.Xipan，2003：2－5，11.

［9］朱 俊，张 玮，钟春欣，等.航道货运量预测方法及其应用［J］.中国港湾建设，2008，156（4）：14－16.

［10］冯宏琳，张 玮，廖 鹏.基于灰色系统理论的船闸货运量预测［J］.武汉理工大学学报：交通科学与工程版，2006，30（1）：810－814.