基于MATLAB的永磁体直线电机的设计
2011-07-07王雪艳
王雪艳
(淄博职业学院,淄博 255314)
0 引言
一台旋转运动的电动机沿着半径方向的剖面图与直线电动机的相同。其简单的结构和运动方式来带了高效率。磁悬浮列车就是用直线电机来驱动的最好的例子。航空母舰上的飞机电磁弹射器也可以使用直线电机(未运用,正处于研究阶段)。目前直线电机的应用已经越来越广泛。本文以永磁电机为例探讨直线电机的工作原理和设计思路。随着计算机技术的发展,电机设计方法的发展日新月异。目前最常用的是用商业的专用软件来进行设计,但是要找到一种既有针对性又符合自己设计风格的软件并不容易,自己编程来辅助设计势在必行。程序需要根据毕奥—萨伐尔定律计算磁场,鉴于计算过程比较复杂,国内的研究成果仅有:兰州大学苟晓凡等学者的《矩形永磁体磁场分布的解析表达式》(国家自然科学重点基金项目)。经本文研究后发现,借助于MATLAB工具强大的公式推导和数值运算能力,只需用简单的程序语句便可计算出数据,然后绘制出直观图像,此法比传统的方法高效简便。MATLAB还提供了各种丰富的工具箱,比如神经网络工具箱、优化工具箱等等,可以很方便地利用它们去进行更深层次的研究。
1 单块矩形永磁体磁场计算
永磁直线电机是由通电线圈和若干块矩形永磁体组成的。要研究直线电机的工作过程,需要先弄清电机磁场的空间分布。一个长、宽、高为a、b、h的矩形永磁体如图1所示。
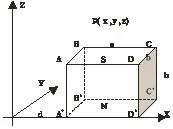
图1 矩形永磁体
其外部空间任一点P(x, y, z)的磁场是由磁体内部分子电流共同叠加而产生的合磁场。当矩形磁体沿一个方向充分磁化并达到饱和后,因磁体内分子电流排列整齐而使磁体内部分子电流全部被抵销,所以可看成只有磁体表面电流在流动。如图1所示,矩形永磁体的A’ B’ C’ D’平面处于XY坐标平面,A’点与坐标原点距离为d,根据磁体NS极性,按右手螺旋定则可知其体表电流沿ABCD方向流动,并且只有四个竖直方向(平行Z轴)的平面有电流流动,而上下两个水平平面(垂直Z 轴)无电流流动。P点磁场的计算只需计算出四个竖直平面电流在P点产生的磁场,然后加起来。
先来计算平面ABB’A’在P点形成的磁场,假设此平面上有一点(xi, yi, zi),可由毕奥—萨伐尔定律来计算(xi, yi, zi)点在P点形成的磁场强度,公式为,式中是沿电流方向的矢量微元。在MATLAB中,用向量来表示它。因为它只有x和y两个方向的分量,可以记为=[dxi,dyi,0],式中r为P (x, y, z)点到(xi, yi,zi)的距离。我们可以将构造成一个MATLAB向量r_matrix,设:
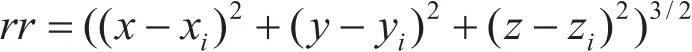
则 r_matrix=[(x-xi)/rr,(y-yi)/rr,(z-zi)/rr],这里需要引入一个面电流密度J=I/h,运算式变换为:记为K,它是一个与磁体材料和尺寸等参数有关的常数。通过实测磁体外某一点的磁感应强度,计算出常数K,上面的公式可转变为:,可编程处理:
clear;
syms x y z xi yi zi dxi dyi dzi K real
rr=((x-xi)^2+(y-yi)^2+(z-zi)^2)^(3/2);
dl=[dxi,dyi,0];
r_matrix=[(x-xi)/rr,(y-yi)/rr,(z-zi)/rr];
dB=K*dzi*cross(dl,r_matrix);
通过如上程序进行符号运算后得到的dB是一个三维向量,dB(1),dB(2),dB(3)三个分量分别代表x,y,z方向的磁感应强度微分元。使用quad2d()函数对ABB’ A’ 整个平面区间进行数值积分得到B,但dB的向量符号表达式中包含有积分变量微元dxi、dyi、dzi,必须去掉后才能用quad2d()函数进行数值积分,如何具体处理这三个积分变量微元呢?这里我们可以根据不同的平面来确定。
1)ABB’ A’ 平面,平行于ZY平面,积分元为dyi和dzi,xi=d,dxi=0,yi变量积分区间为[0,b],zi变量积分区间为[0,h]。处理方法如下:把dB向量中的三个积分元做一个替换,dxi替换为0,dyi和dzi分别替换为1,相当于先得到dB/(dyidzi)的符号表达式,然后用quad2d()函数进行积分。
2)BCC’ B’ 平面,平行于 ZX平面,积分元为dxi和dzi,yi=b,dyi=0,xi变量积分区间为[d,d+a],zi变量积分区间为[0,h]。
3)CDD’ C’ 平面,平行于ZY平面,积分元为 dyi和 dzi,xi=d+a,dxi=0,yi变量积分区间为 [b,0],zi变量积分区间为[0,h]。
4)DAA’ D’ 平面:平行于ZX平面,积分元为 dxi和 dzi,yi=0,dyi=0,xi变量积分区间为 [d+a,d],zi变量积分区间为[0,h],编程如下:
syms a b d h real
%ABB'A'平面 xi=d, dxi=0, dyi=1, dzi=1
dB_AB_div_dyidzi=subs(dB,{xi,dxi,dyi,dzi},{d,0,1,1});
%BCC'B'平面 yi=b, dxi=1, dyi=0, dzi=1
dB_BC_div_dxidzi=subs(dB,{yi,dxi,dyi,dzi},{b,1,0,1});
%CDD'C'平面 xi=d+a, dxi=0, dyi=1, dzi=1
dB_CD_div_dyidzi=subs(dB,{xi,dxi,dyi,dzi},{d+a,0,1,1});
%DAA'D'平面 yi=0, dxi=1, dyi=0, dzi=1
dB_DA_div_dxidzi=subs(dB,{yi,dxi,dyi,dzi},{0,1,0,1});
此后对四个面的表达式进行合并处理,YZ平面的总磁感应强度dByz由ABB'A'平面和CDD'C'平面相加得到,考虑两平面电流方向相反,为了把yi的积分区间统一为0到b, 相加时把CDD’ C’段加负号,同样XZ平面的总磁感应强度dBxz由BCC’ B’ 平面和DAA’ D’ 平面两部分相加得到,把DAA’ D’ 段也反一下符号,使xi的积分区间统一为d到d+a。对dByz和dBxz分别进行数值积分后再相加,就得到P(x, y, z)点磁感应强度B。为了先求出常数K,测量出磁体表面或者外面一点的磁感应强度是必要的。比如测量出ABCD平面中心点外0.5mm处Z方向的磁感应强度Bz0为0.1T,然后令K=1,计算出Bz,则K=Bz0/Bz, 假设磁体的参数为:a=50mm,b=500mm,h=10mm。下面给出计算程序:
dByz=dB_AB_div_dyidzi-dB_CD_div_dyidzi
dBxz=dB_BC_div_dxidzi-dB_DA_div_dxidzi
a=50;b=500;h=10;d=0;Bz0=0.1;x=a/2;y=b/2;z=1 0.5;K=1;
dBz1=vectorize(char(subs(dByz(3))));%YZ平面在中心处的磁感应强度
dBz2=vectorize(char(subs(dBxz(3))));%XZ平面在中心处的磁感应强度
下面要对dBz1和dBz2进行积分。先用sprintf()函数构造出符号运算表达式,然后再放到eval()中去运算得到结果。
Bz1=sprintf('quad2d(@(yi,zi)%s,0,b,0,h)',dBz1);
Bz2=sprintf('quad2d(@(xi,zi)%s,0,b,0,h)',dBz2);
f=sprintf('%s+%s',Bz1,Bz2); %f为XZ和YZ两个平面Z方向磁场总和
K=abs(Bz0/eval(f));
接下来,可以利用前面所推导出的符号表达式,进行诸多分析设计。比如要计算分析ABCD平面上在y=b/2,z=10.5处X方向和Z方向的磁场沿坐标X的分布图,可用如下程序,绘制图像如图2所示。
Syms x real;
dBxzz1=vectorize(char(subs(dBxz(3))));
Bxzz1=sprintf('quad2d(@(xi, zi)%s,0,a,0,h)',dBxzz1);
dByzz1=vectorize(char(subs(dByz(3))));
Byzz1=sprintf('quad2d(@(yi,zi)%s,0,b,0,h)',dByzz1);
f=sprintf('%s+%s',Bxzz1,Byzz1);
fun=eval(['@(x)',f]);
xx=-20:70;
Bz1=arrayfun(@(x) fun(x),xx);
dBx1=vectorize(char(subs(dByz(1))));
Bx1=sprintf('quad2d(@(yi,zi)%s,0,b,0,h)',dBx1);
fun=eval(['@(x)',Bx1]);
Bx1=arrayfun(@(x) fun(x),xx);
plot(xx,Bx1,xx,Bz1)

图2 Bx1、Bz1磁场分布曲线图
通过计算得出磁场的空间分布图。如要求出ABCD平面上方0.5mm的Bz分布,编程如下:
syms x y real;
dBxzz1=vectorize(char(subs(dBxz(3))));
Bxzz1=sprintf('quad2d(@(xi,zi)%s,0,a,0,h)',dBxzz1);
dByzz1=vectorize(char(subs(dByz(3))));
Byzz1=sprintf('quad2d(@(yi,zi)%s,0,b,0,h)',dByzz1);
f=sprintf('%s+%s',Bxzz1,Byzz1);
fun=eval(['@(x,y)',f]);
xx=0:50;yy=0:500;
[X,Y]=meshgrid(xx,yy);
Bz=arrayfun(@(x,y) fun(x,y),X,Y)
plot3(X,Y,Bz)
上面程序绘出的图像如图3所示。
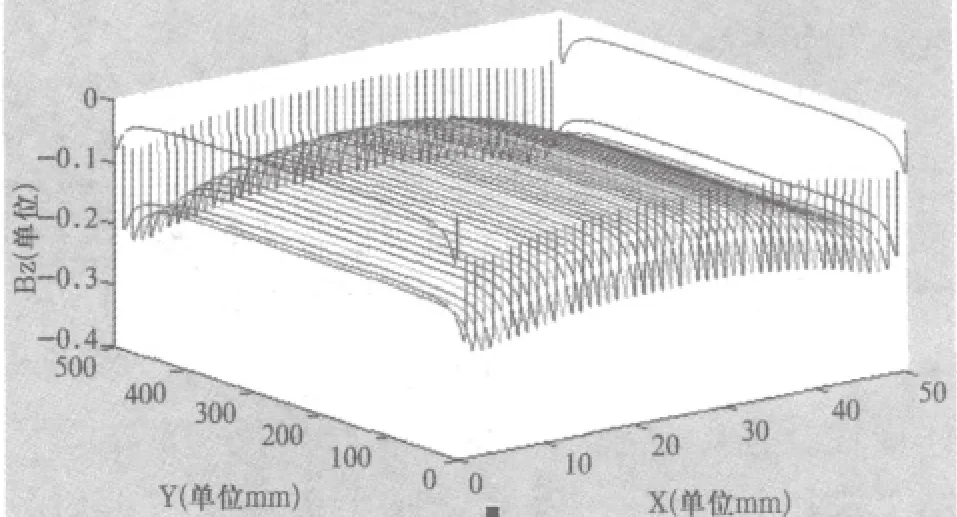
图3 磁体表面Bz三维分布图
如图3所示,在磁体表面附近的Bz较强,而远离磁体表面的Bz迅速减小。因此,在制作电机时,应让通电线圈尽量靠近磁体表面位置以获得强大的磁场力。一般放在表面0.5mm上方。
2 多块永磁体磁场中线圈受力计算
直线电机是由多块尺寸相同的永磁体按一定间距并排,并且相邻的两块极性相反而构成的。如图4所示。
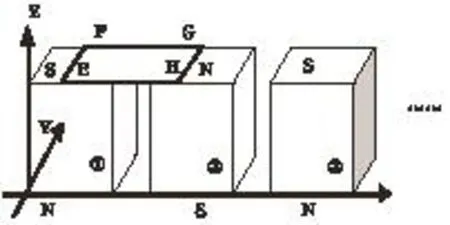
图4 多块磁体排列示意图
假设各磁体之间距离为c,在磁体上方放置一个平行于磁体顶端面的通电线圈EFGH,线圈EF边长b,FG边长=a+c,线圈距离磁体表面0.5mm,假设电流I沿线圈FGHE方向流动,现在来分析线圈沿X轴方向所受的磁场力Fx,磁场力可以根据进行计算。由于磁体的对称性,沿X轴向位于磁体中心线两侧的B是对称的,而GF边和EH边电流相反,所以两侧边导线受力抵销,只需计算导线GH和EF上的受力,并且只要计算出了EF段的磁场力,可通过坐标平移变换得出GH导线段的受力。下面就来对EF的受力进行计算:电流沿Y方向流动,=I×[0,dy, 0]×[Bx, By, Bz],可以推导出dFx= -I×Bz×dy,这里的Bz是多块磁体在Z方向的磁场总和。根据此式,通过数值积分就能得到Fx,并画出其在X方向的变化曲线图。dy积分区间应该沿电流方向,在[0,b]区间。
现在以8块磁铁为例来编程说明,对于各磁体的磁场先分别计算,再累加起来。各磁体主要差别在X轴上放置的位置不一样,就是前面求出的dB向量表达式中的d参数不同,另外还有偶数位置的磁体极性反向,也就是向量正负号要反向。第1块磁铁放在坐标原点处d=0,第2块d=a+c,第3块d=2 (a+c),第i块磁铁d=(i-1) (a+c)。写出程序如下:
Syms c d x y real;
p=-1;dByzz=0;dBxzz=0;
for i=1:8;
p=-p;
dd=(i-1)*(a+c);
dByzz=dByzz+p*subs(dByz(3),d,dd);
dBxzz=dBxzz+p*subs(dBxz(3),xi,xi+dd);%
此处对xi坐标变换,以便将积分区间由[d,d+a]变为[0, a]
end
上面这段程序得出的dBxzz和dByzz分别是8块磁铁在XZ平面和YZ平面Z方向的总磁感应强度的微分符号表达式。下面进一步计算Fx,程序仍然使用前面的磁体参数,假设I=2A。
a=50;b=500;h=10;d=0;z=10.5;c=5;
dBxzz=vectorize(char(subs(dBxzz)));
Bxzz=sprintf('quadl(@(yy) arrayfun(@(y)quad2d (@(xi,zi)%s,0,a,0,h),yy),0,b,0.1)',dBxzz);
dByzz=vectorize(char(subs(dByzz)));
Byzz=sprintf('quadl(@(yy) arrayfun(@(y)quad2d(@(yi,zi)%s,0,b,0,h),yy),0,b,0.1)',dByzz);
f=sprintf('%s+%s',Bxzz,Byzz)
fun=eval(['@(x)',f]);
xx=0:300;I=2;
Fx=-I*(arrayfun(@(x) fun(x),xx));
这里得出的Fx是一维向量,坐标变化单位为1mm,如图5所示。
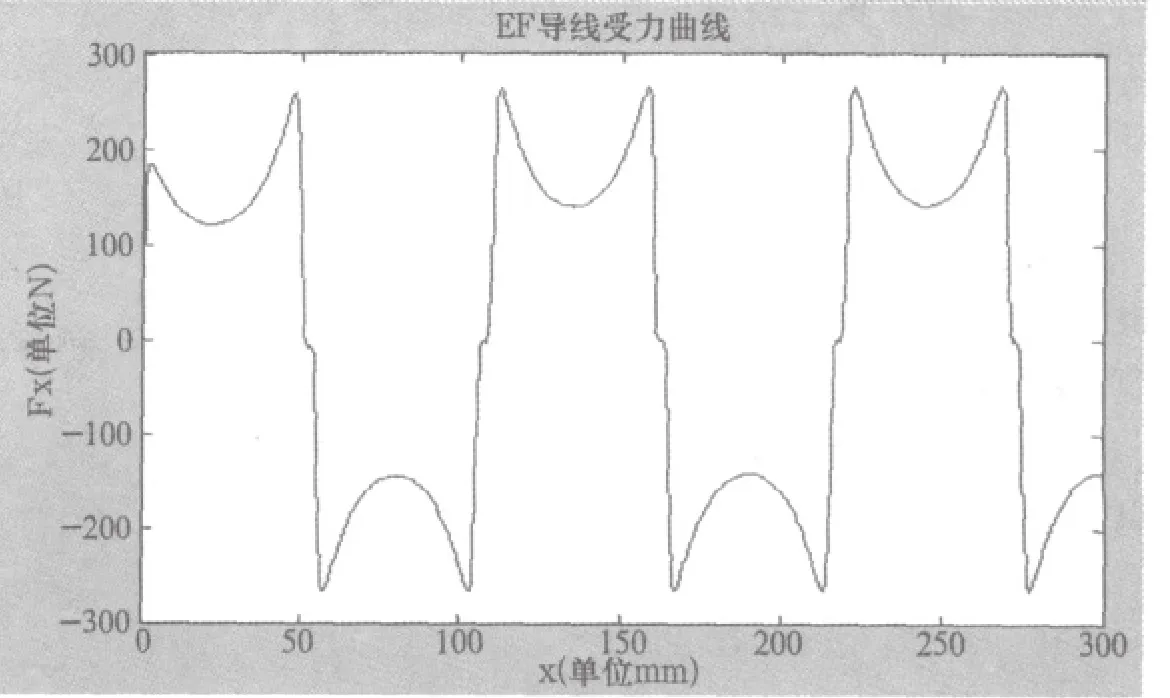
图5 线圈EF段导线受力曲线图
GH段受力计算通过坐标变换x=x+a+c,由于电流反向,-Fx(x+a+c),所以线圈总的受力为F=Fx (x) -Fx(x+a+c),绘制图像如图6所示。
3 结论
1) 如图6所示,线圈的受力是不断正负变化的。为保证线圈沿X轴方向持续运动,需在F变为负值时及时将线圈中的电流反向一次,这样就能使线圈的受力始终为正值,大小等于| F |。现代电子技术的发展使得对电流的控制非常精确,制造直线电机也变得比以往更加容易。电机由旋转运动回归到直线运动,从而带来更高的效率。
2)多个线圈的共同应用使受力变得平滑。只需要根据位置做坐标变换就可以对多个线圈进行分析,不用重复计算。另外,由于磁场的对称性,只需要计算前四块磁铁的情况。
3) 本文通过改变磁体的参数分析磁场力与各参数之间的关系曲线。MATLAB编程的使用使得最优化设计方案的寻求更为方便。
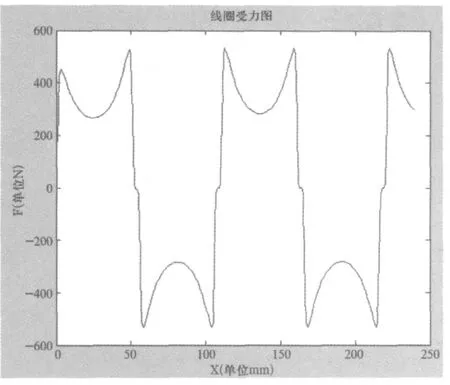
图6 线圈受力图
4) MATLAB是一种解释型语言。虽然运行效率不高,但可以通过优化、使用并行运算等方法来提高速度,还可以通过改变分析计算的计算精度、取样点间距等来提高运行速度。本文程序在MATLAB R2009b上运行通过。
5)为了验证磁场分布计算的正确性,将本文计算结果与美国希捷公司高级顾问工程师侯春洪博士设计软件计算绘制的图表进行对比,其一致性证明了本文研究方法和程序运算的真实性和可信度。
[1] 苟晓凡, 杨勇, 郑晓静. 矩形永磁体磁场分布的解析表达式[J]. 应用数学和力学, 2004,25(3).
