基于自适应模糊的印刷色彩质量控制及Simulink仿真

康建山，初红艳，杨俊敬

（北京工业大学 机电学院，北京 100124）

0 引言

随着智能控制的不断发展，模糊控制以其无需建立系统数学模型、对参数变化不敏感、与其他控制方法具有很强的融合性等特点被大量应用于实际的生产管理控制当中。如模糊PID控制、模糊神经网络控制、模糊自适应控制等在应用中都取得了显著的控制效果[1]。

由于印刷机印刷过程的传递函数难求、检测数据少且要求调整快速等特点，同时这类大滞后非实时系统的工艺条件受工作环境影响而容易出现色彩质量偏差等问题。传统控制方法多是基于人工调整，受人为因素影响。本文提出了基于自适应模糊控制方案，利用墨键—密度控制曲线得到其控制规则，并根据生产过程中的检测数据对控制规则系数进行修正，较快地提高了控制精度，减少调整次数。

1 问题描述及解决方案

印刷品的色彩质量可由其实地密度体现，而其主要的影响因素是给墨量的多少。现代生产中主要通过控制步进电机调整墨键开度以控制给墨量。目前多数中高档印刷机都配置了油墨预置功能，该预置数据主要由实验数据得到，但是受到实验条件的约束，实际生产过程中，需要人工修正墨键开度大小以调整色彩质量。

由于印刷机的印刷过程需要一定的稳定时间，同时印刷机色彩质量检测属于离线检测且要求快速调整达到期望，因此常规调整很难达到规定要求，需要考虑新的色彩质量控制方法。

1.1 墨键—密度控制曲线

墨键—密度曲线表示在某特定工作条件和网点面积率条件下，不同墨键开度与其对应的印刷品实地密度关系曲线。虽然影响印刷质量的因素除了给墨量，还有其工艺因素如温度、印刷压力、速度以及油墨粘度等[2]，但是由于印刷过程的连续性，其生产工艺影响在一定范围内，所以墨键—密度控制曲线的总体趋势保持不变。

实际生产中应用的曲线在要求的精度范围内大都能用二次曲线来拟合。设期望实地密度为R，将墨键—密度控制曲线表示为

将墨键—密度控制曲线在初始墨键开度xo处泰勒展开得到

式中：xo—当前墨键开度；

f(xo)—墨键xo对应的实地密度值；

xs—调整后得到的墨键开度；

f(xs)—墨键开度xs时对应的实地密度；

f '(xo)—墨键xo处的斜率。

因此可以利用墨键—密度曲线来取得期望实地密度下的墨键开度值，并通过对控制曲线一定规律的调整以适应工艺条件的变化，并实现色彩质量的控制。

1.2 自适应模糊控制方案

由于模糊控制更接近人的思维方法和推理习惯，因而适用于非线性、大滞后的印刷过程控制中。而且通过其控制规则的自适应调整，使得控制规则对工艺条件的适应性更强。

一般自适应模糊控制器的控制框图如图1所示。

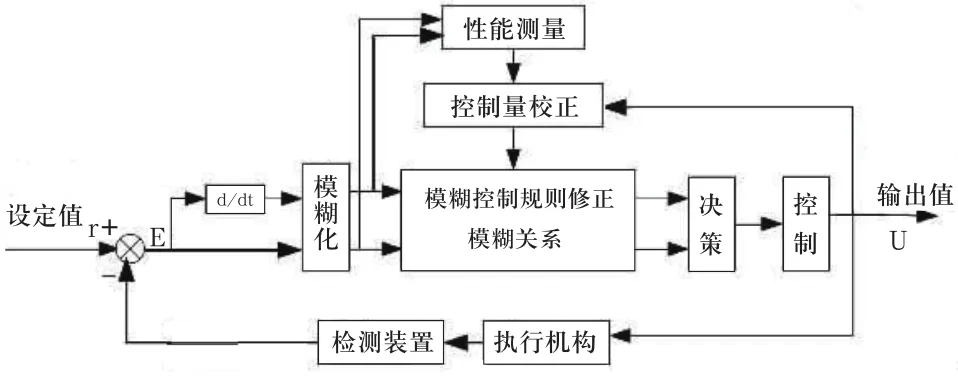
图1 自适应模糊控制框图

自适应模糊控制器在简单模糊控制器的基础上增加了三个功能块，即性能测量、控制量校正和控制规则修正，其中性能测量用以衡量设定值的偏离情况；控制量校正部分将设定值所需要的校正量转换为对控制量的校正量；控制规则校正根据控制量校正所得到的校正量修正控制规则表中控制量，使控制规则更加合理，使系统的输出朝期望的方向变化[3]。

因此，根据式（2）可以方便的得到基于T-S模型的控制规则。同时，利用控制器的自适应功能，可以调整控制规则以适应生产条件的变化，达到期望的控制效果。

2 模糊控制器设计

根据对问题的描述，设计墨键控制自适应模糊控制器控制图如图2所示。

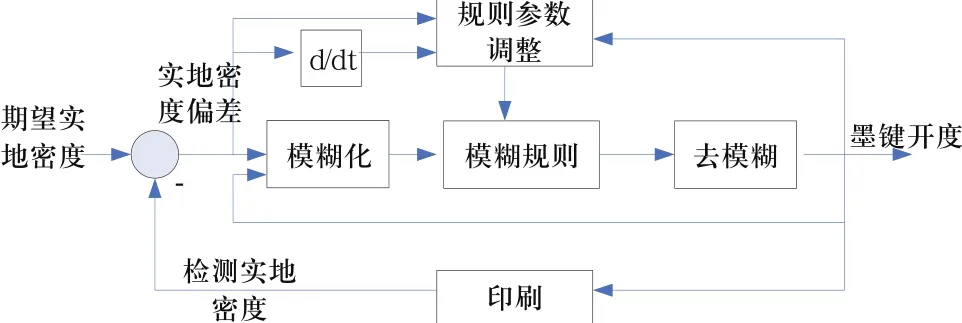
图2 墨键控制自适应模糊控制框图

通过对印刷品实地密度的检测，利用其与期望实地密度的偏差和当前的墨键开度作为模糊控制器的输入，得到调整后的墨键开度，同时根据实地密度偏差及其变化对控制器控制规则进行调整。

2.1 隶属度函数及去模糊方法的选择

根据经验确定实地密度偏差的论域为[-0.5 0.5]，墨键开度的论域为[0 70]。采用三角形隶属度函数，实地密度偏差和墨键开度的隶属度函数分别如图3和图4所示。

图3 实地密度偏差的隶属度函数

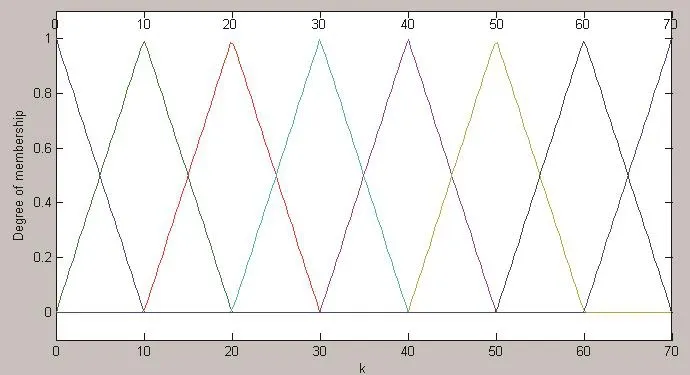
图4 输入墨键开度的隶属度函数

采用重心法作为去模糊方法，模糊系统的输出量为每条规则的输出量的加权平均[4]：

2.2 控制规则的确定

根据一般经验总结，当实地密度偏差大时，墨键开度的调整也应随着大些，反之调整量小；同时，在同样实地密度偏差情况下，墨键开度调整量又与当前墨键开度有关；当实地密度偏差小于允许偏差时墨键开度不需要调整。

T-S模型能够方便地进行非线性系统建模和设计，其第j条控制规则可描述如下：

其中x1，x2为输入变量，在印刷机色彩质量控制中为实地密度偏差和墨键开度值，A1，A2分别为两个输入变量的模糊语言值。

由公式(2)易知，控制规则中p0=0，p2=1，p1=1/f'(x)，系数p1的取值可根据输入墨键开度值确定，因此需要根据墨键—密度控制曲线确定控制规则系数p1的参数表，并由此参数表选择特定条件下的系数值。

2.3 控制规则参数表的调整

为适应工艺条件的变化，控制规则参数表需要根据检测实地密度偏差作出相应调整。设墨键开度初始值为xo，墨键开度为xt时对应期望实地密度R。第一次检测得到实地密度偏差为eo，如果未达到要求，需要对墨键开度进行eo/f'(xo)的调整，调整后墨键开度为xs，再次印刷后检测到的实地密度偏差e1。如果偏差仍未达到要求，则需要第二次墨键调整，同时也说明受各种影响因素的影响，实际的墨键—密度曲线发生变化，斜率需要进行校正，而控制规则参数p1包含了斜率的所有信息，因此只需要对p1进行调整。

设ft'(xo)表示xo处斜率调整后的斜率值。调整方法如下：

由公式(2)得

将公式（4）代入公式（5）可近似得

3 仿真

以印刷机的墨键控制为例，利用matlab对控制算法进行仿真验证。通过实验得到某印刷机在某工艺条件下网点面积率为50%的墨键—密度数据表如表1所示。

表1 网点面积率50时墨键—密度表

通过对实验数据进行二次曲线拟合得到的墨键—密度控制曲线为

根据控制曲线得到网点面积率50%的控制规则参数表，即系数p1的参数表，如表2所示。如果将其他网点的控制规则参数表也添加到表2中，就可以得到总的控制规则参数表。

表2 网点面积率50的控制规则参数表

利用Matlab中的Simulink模块构建仿真框图如5所示

图5 印刷机墨键自适应模糊控制框图

其中：respect模块指定期望实地密度值，这里设为1.5；fadapt模块为S-Function[5]，其中包含了控制规则参数表，以及相应的自适应模糊控制算法；condition模块是现场的生产加工曲线，即实际的输入输出关系，假设为

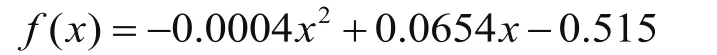
墨键开度的初始值根据以往实验结果设置为30，控制规则参数表如表2所示。下面进行三种仿真。

3.1 利用原始控制规则参数表进行墨键控制

第一次检测实地密度偏差为0.413，利用原始规则参数表2对墨键开度进行调整后，得到墨键开度为38，印刷后检测得到实地密度偏差为0.1074。再次利用原始参数表调整得到墨键开度40，印刷后实地密度偏差0.0352，达到允许偏差，其实地密度调整效果如图6所示。

3.2 利用本文的控制规则参数自适应调整算法进行墨键控制

由于墨键开度初始值为30，印刷后检测得实地密度偏差为0.413，利用原始参数表2，进行第一次墨键开度调整，得到墨键开度为38，印刷后检测得到实地密度偏差为0.1073，未达到期望范围，得知控制规则参数未能很好地反应实际情况。利用调整算法进行规则参数调整后，再对墨键开度进行调整得到41，检测得到实地密度偏差为0.006，密度调整效果如图7所示。控制规则参数表调整如表3所示。

图6 控制规则参数不调整的密度调整效果

图7 参数自适应调整算法的密度调整效果

表3 网点面积率50的调整后规则参数表

3.3 利用调整后的规则参数表进行墨键控制

将调整后的参数表3作为原始规则参数表。首次检测得到实地密度偏差为0.413，经过一次墨键调整便得到41，实地密度偏差为0.006，符合规定要求，不需参数表调整，得到的实地密度调整效果如图8所示。

图8 利用调整后规则参数的调整效果

通过以上三种仿真，可以看出方法2要优于1，而且方法3经一次调整就能达到要求。说明通过对控制规则参数的调整，能较快的达到控制效果，而且其调整结果较符合实际情况。

4 结束语

针对印刷机的印刷过程具有非实时、大滞后且检测数据少的特点，分析其控制输出不能很好地跟踪实际生产条件的问题，提出了利用自适应模糊控制的方法，通过对控制规则参数的调整达到调整控制曲线进而实现色彩调整的目的。利用matlab对胶印机墨键控制进行仿真，验证该方法在控制曲线趋势不变条件下收敛稳定，且调整速度快；并且在实际应用中，该算法运算简单，易于实现。

[1] 文生平,赵国平.一种变论域模糊控制自适应算法[J].控制理论与应用,2009,26(3):265-268.

[2] 刘世昌.印刷品质量检测与控制[M].印刷工业出版社,2000.[3] 章卫国,杨向忠.模糊控制理论与应用[M].西北工业大学出版社,2000.

[4] 张豪.基于单片机的模糊控制在节水灌溉控制系统中的实现[D].江南大学,2007:17-25.

[5] 费春国.模糊自调整控制器的研究及应用[D].天津科技大学,2003:19-28.