纹理保持的图像去噪
2011-07-06贾瑞芝任丽莎刘瑞华
贾瑞芝,任丽莎,刘瑞华
(重庆理工大学数学与统计学院,重庆 400054)
一般情况下,人们观测到的图像都带有噪声。噪声会导致图像的质量下降,影响图像的视觉效果,因此去除噪声是图像处理的重要研究内容之一[1-2]。然而在图像去噪过程中,图像的重要特征(比如纹理)会被毁坏。常见的噪声有高斯噪声、椒盐噪声和Poisson噪声等。
近年来,变分去噪的方法[3-10]被广泛应用。其中最经典的模型是ROF模型[3],它是由Rudin等于1992年提出的,即:给定一幅含有高斯噪声的图像f定义在Ω⊂R2,要求从f中修复出真实图像u。他们提出了下面的极小化问题:

这里:λ是一个正参数;第1项是正则项,起光滑噪声的作用;第2项是保真项,是为了保证去噪后的图像和原图像偏差不会太大。上面模型在去除噪声的同时保持了图像的边界。然而,当λ很小时,正则项会过度光滑图像,使得图像的部分纹理细节被毁坏,并且,在ROF模型中,由于λ是全局参数,不是局部参数,同样会导致部分纹理被毁坏。
对于其他含有全局参数的变分模型也存在相同的问题,即在图像去噪过程中,这些模型在光滑噪声的同时去掉了部分纹理,这样修复出来的图像和真实图像就有偏差。
黎芳等[4]通过引入一个纹理检测函数改进了ROF模型的保真项,克服了以上变分模型的缺点。本文的模型就是基于黎芳等的思想,重新构造ROF模型的保真项,以实现图像去噪和保持纹理的目的。
1 相关工作
黎芳等利用纹理检测函数改进了ROF模型的保真项,提出了下面的能量泛函极小化问题[4]:
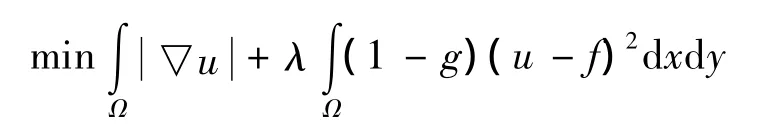

其中
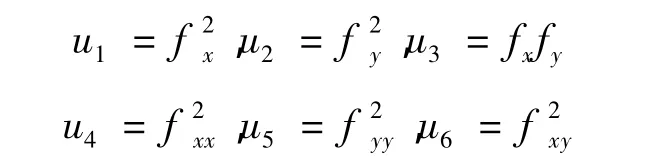
需先经TV光滑去噪,即
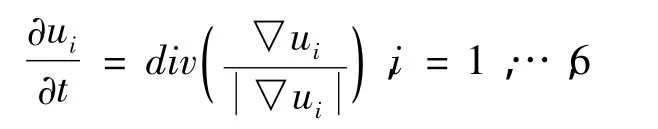
从g函数的构造可以看出:在光滑部分,6个通道都趋于0,使得g趋于1,这时模型的正则项起主要作用,故光滑了图像的噪声;在纹理部分,由于至少有一个通道趋于无穷,使得g趋于0,这时模型的保真项起主要作用,而且这个模型中的λ是个相对比较大的参数,故可以保持图像的纹理。在上面这个模型中,λ(1-g)是一个局部参数,故克服了阶梯效应。
Chao等[5]构造了一个新的纹理检测函数,通过异性扩散的方法实现了图像的去噪。这个纹理检测函数是由局部梯度和灰度级方差构成。梯度是检验图像纹理的一个重要指标,梯度的模越大,纹理越明显,然而,在梯度的模小的地方也可能存在小的纹理细节。为了能检验出更多的纹理,Chao等人引入灰度级方差构造了下面这个纹理检测函数:
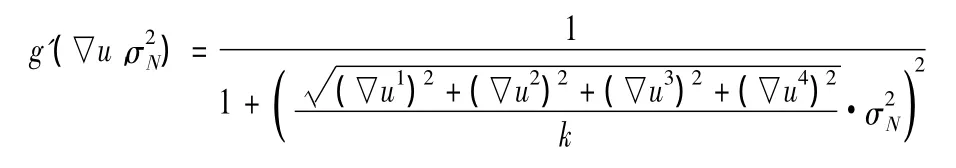
其中,灰度级方差是由一个3×3的邻域窗口计算出的:

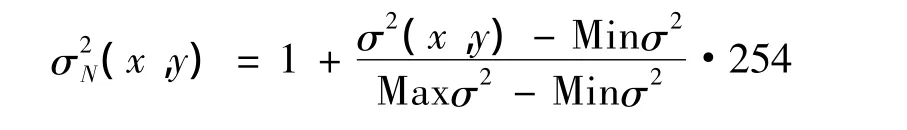
灰度级方差的优点是:即使在梯度相差不大的地方,它的灰度级方差也会相差很大,因此可以检测出小的纹理细节。
另外,▽ui,i=1,2,3,4 是这个窗口的上、下、左和右4个方向的梯度。
本文将利用这个纹理检测函数代替改进的ROF模型中的纹理检测函数来实现图像去噪和保持纹理的目的。
2 模型的提出
由本文分析可知,利用纹理检测函数g'可重新构造ROF模型的保真项,另外又增加了一项保真项,得到如下的模型:
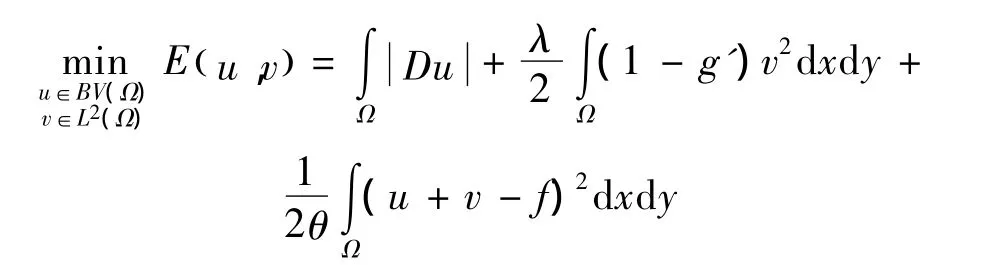
其中:λ和θ都是正参数;f是观测到的含有噪声的图像;u是去噪后的图像;v是噪声图像。在卡通部分,g→1,正则项和第2个保真项起主要作用,正则项可以去除噪声,第2个保真项可以保证修复出的两幅图像之和不会与原图像偏差太大。在纹理部分,g→0,由于λ比较大,所以第1个保真项起主要作用,这时纹理就被保持在去噪后的图像u中。因此本文模型不仅可以去除噪声,而且可以有效的保持部分纹理信息。
u的最小值和v的最小值可通过求解下面的演化方程

的稳态解得到。
3 数值实现
在下面的实验中,空间、时间步长均取为1,迭代次数为30次,在本模型中纹理检测函数g'中的参数为:k=10;λ =0.1,θ=0.01。
针对在原始图像中加入方差为σ=0.03高斯噪声的图像进行仿真实验,分别利用ROF模型、改进的ROF模型与本模型实验结果进行比较。
图1和图2为3种模型处理的结果。由图1(d)和图2(d)可以看到ROF模型在去噪的过程中大量的纹理信息丢失。从图1(e)和图2(e)可以看到改进的ROF模型去噪效果得到了很大的改进,保持了图像原有的大量信息。但与图1(f)和图2(f)比较,可以看出本模型去噪后的图像保持了原图像更多的信息,如图1(f)与图1(e)比较,Barbara头巾上的纹理和她背后椅子上的纹理更清晰。为了进一步说明本模型的有效性,笔者使用信噪比对3个模型进行比较,信噪比越大说明效果越好。从信噪比的比较也可以看出本模型的去噪效果较好。

图1 Barbara图去噪的结果与比较

图2 Lena图去噪的结果与比较
4 结束语
本文提出了一个新的图像去噪模型,通过与ROF模型和改进的ROF模型比较,可以看出本文提出的模型在去除噪声的同时,能很好地保持图像的部分纹理。但是,还有部分纹理细节在图像去噪过程中丢失,这就要求在以后的工作中进一步改进模型以实现在去噪过程中保持图像纹理的目的。
[1]吴昌东,江桦,邱晓初.基于多级中值滤波——提升小波技术的图像去噪[J].激光杂志,2010,31(6):23-24.
[2]刘广东,陈阿林.基于Curvelet变换的图像去噪[J].重庆师范大学学报:自然科学版,2009,26(4):86-89.
[3]Rudin L,Osher S,Fatemi E.Nonlinear total variation based noise removal algorithms[J].Physica D,1992(60):259-268.
[4]Li F,Shen C,Shen C L.Variational denosing of partly textured images[J].JVCI R,2009(20):293 -300.
[5]Chao S,Tsai D.An improved anisotropic diffusion model for detail and edges– preserving smoothing[J].PRL,2010(21):2012-2023.
[6]Aubert G,Aujol J.A variational approach to remove multiplicative noise[J].SIAM J Appl Math,2008,68(4):925-946.
[7]Gilboa G,Sochen N,Zeevi Y.Variational denoising of partly textured images by spatially varying constraints[J].IEEE Trans.Image proc,2006(15):2281 -2289.
[8]Nikolova M.A variational approach to remove outliers and impulse noise[J].JMIV,2004,20(1/2):99 -120.
[9]Vese L,Osher S.Image denoising and decomposition with total variation minimization and oscillatory functions[J].JMIV,2004,20(1):7 -18.
[10]Bresson X,Esedoglu S,Vandergheynst P.Fast global minimization of the active contour/snake model[J].Math Imag Vis,2007,28(2):151 -167.
[11]肖蕾,何坤,周激流,等.改进自适应中值滤波的图像去噪[J].激光杂志,2009(2):44 -46.
