一种改进的BFGS算法及其收敛性分析

陈奎林

(重庆大学数学与统计学院，重庆 401331)

1 问题的提出

本文针对无约束最优化问题:minf(x)，x∈Rn开展研究，其中f:Rn→R是一个连续可微的函数。拟牛顿算法中的BFGS算法是一类解决无约束最优化问题的有效算法，这类算法的关键是Bk的选取，不同的选取方式，对应不同的BFGS算法。

为了使算法更具优越性，文献［1－5］在传统的拟牛顿方程的基础上提出了一个新的拟牛顿方程，即，其中是一个对称正定矩阵，从而得到了一类改进的BFGS方法，其迭代公式为

受以上思想的启发，提出了Ak的一种选取方法，即Ak=‖gk+1－gk‖I，进而提出了一类新的BFGS算法，并证明了它的全局收敛性和超线性收敛性。

本文采用的搜索准则(Wolfe准则)为:

其中0＜σ1＜σ2＜1。

改进的BFGS算法步骤:

步骤1 给出初始点x0∈Rn和初始对称正定矩阵B0∈Rn×n，令ε＞0，k=0。

步骤2 若梯度函数在迭代点xk处满足‖gk‖≤ε，则停止;否则计算Bkdk+gk=0，求出搜索方向dk。

步骤3 利用Wolfe准则求得步长αk，令xk+1=xk+αkdk。

步骤4 计算Ak=‖gk+1－gk‖I，并代入 式(1)，修正Bk得Bk+1。

步骤5 令k:=k+1，转步骤2。

2 收敛性证明

为证明算法的全局收敛性和超线性收敛性需要以下假设:

①f(x)是二阶连续可微的，x*是f(x)的极小点。

②水平集Ω={x|f(x)≤f(x0)}是有界凸集，其中x0是给定的。

③f(x)在凸集Ω上连续可微，且存在一个常数L＞0，使得下式成立:

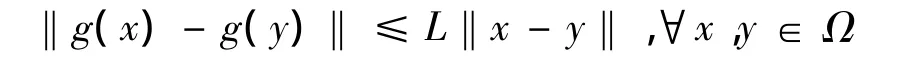
其中:g(x)=▽f(x);‖·‖是Euclidean范数。

④f(x)一致凸，即存在常数m和M，使得

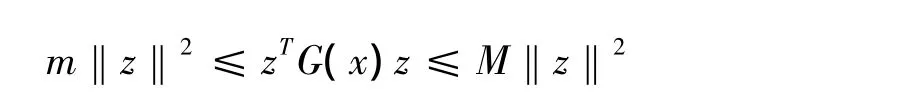
这里∀x∈Ω，z∈Rn，其中 G(x)是 f(x)的海色矩阵。

⑤ G(x)在Ω上Lipschitz连续。即存在L'＞0使得∀x，y∈Ω，有

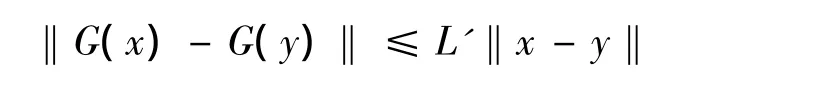
由上面的假设容易得到

2.1 全局收敛性证明

引理1［4］对任意给定的 k 和由改进的 BFGS 算法产生的(α，x，g，d)，若＞0，那么

kk+1k+1k+1Bk+1正定。

引理2 若假设(a)、(b)、(d)成立，由改进的BFGS算法产生的点列为 {xk}，则，其中sk=xk+1－xk。

证明由Taylor公式，

由假设④及式(2)有

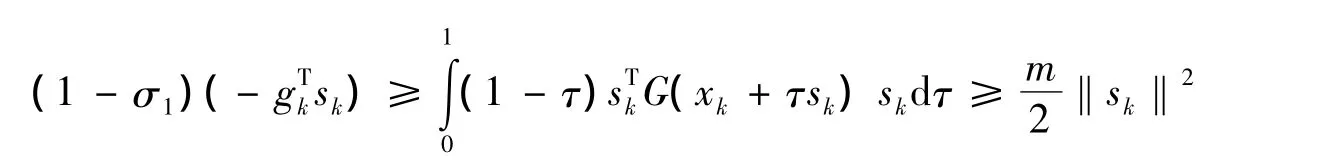
引理3 若假设②～④成立，则式(4)(5)成立

证明

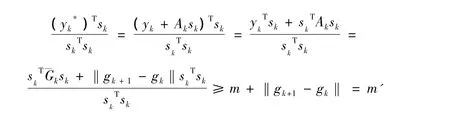
定理1 设x0为任意初始点，f(x)在Ω上满足假设(a)，(d)，则对任何对称正定矩阵B0，由改进的BFGS算法产生的点列 { xk}收敛到f(x)的极小点x*。

证明记，由引理 3 可知 mk≥m'，Mk≤M'。

对式(1)有

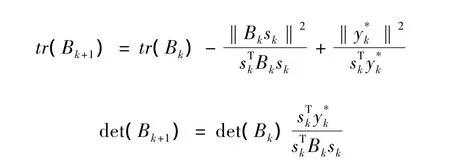
令 ψ(Bk+1)=tr(Bk+1)－ln(det(Bk+1))，则有

因为函数p(t)=1－t+lnt对任意的t＞0都是非正的，所以有

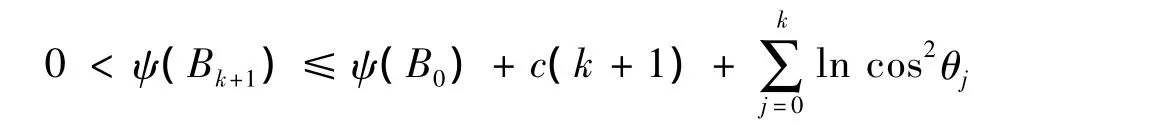
不失一般性，假设 c=M'－ lnm'－1 ＞0，cosθj→0，那么存在 k1＞0，使得对∀j＞ k1都有 ln cos2θj＜ －2c，所以

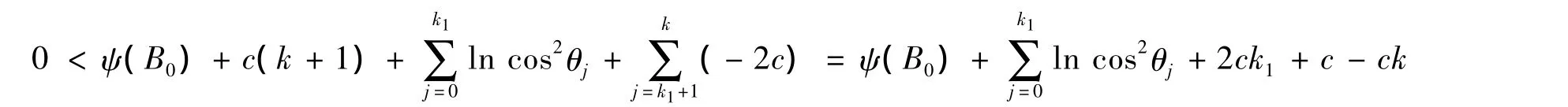
当k充分大时，上式右端的值为负，与左端矛盾，所以假设不成立，从而存在一个子序列 {jk}，使得cosθjk≥ε＞0。而由文献［1］中式(3.14)可知lim inf‖▽fk‖→0。又因为目标函数是凸的，所以由改进的BFGS算法产生的点列 { xk}收敛到f(x)的极小点x*。

2.2 超线性收敛性证明

引理4 若{ xk}是由改进的BFGS算法产生的点列，且假设(c)成立，则

证明由 Taylor公式，有 gk+1－ gk=G(ξk)sk，其中 ξk=xk+ σsk，σ∈(0，1)。所以 ‖Ak‖=‖gk+1－gk‖≤L‖sk‖，再结合引理2可知成立。

定理2 在假设①～⑤成立的前提下，设以1作为试探步长的Wolfe步长规则下改进的BFGS算法产生的迭代序列 { xk}收敛到最优解x*，且满足，则 { xk}超线性收敛到x*。证明过程类似于文献［1］的描述。不再赘述。

［1］王宜举，修乃华.非线性规划理论与算法［M］.陕西:科学技术出版社，2008.

［2］王安平，马烁，赵天玉.一种改进的BFGS算法及其全局收敛性分析［J］.河北科技大学学报，2009，30(1):8－10.

［3］张恒，何伟.基于新拟牛顿方程的改进BFGS方法［J］.淮海工学院学报，2007，16(3):10－12.

［4］WEI Zengxin，LI Guoyin，QI Liqun.New quasi-Newton methods for unconstrained optimization problems［J］.Applied Math and Comp，2006，175:1156 －1188.

［5］Jorge Nocedal，Stephen J.Wright.Numerical optimization［M］.［S.l.］:Springer，1999.