电控楔形离合器系统动力学建模与响应分析

霍 易 陈 俐

(上海交通大学汽车电子控制技术国家工程实验室,上海200240)

1 电控楔形离合器介绍

当前主流的自动变速器均采取电液控制系统,即通过电磁液压控制阀改变作用在离合器活塞缸上的油压,进而控制换挡离合器结合时间和结合作用力。然而,由于该变速器工作时需要发动机带动油泵持续转动,以提供高油压,所以从节能环保的角度讲,液压作动的自动变速器不是一个很好的选择。如今,汽车系统电气化已经成为汽车技术发展的主要趋势,电动执行机构广泛应用于汽车系统之中,例如发动机的电子节气门,DCT的电机驱动的换挡执行机构和电力制动(E-brake)等。本论文中介绍的电控楔形离合器来源于对通用6T45型号自动变速器的一个离合器执行机构进行电气化改造项目,将原来液压作动方式变成电控作动方式,即利用伺服电机驱动一个楔形块机构,推动离合器,实现换挡。

与传统AT的液压作动式离合器相比较,电机驱动式的有如下优点：

1)液压作动离合器需要一个持续工作的液力泵提供高压,因此作为动力源的发动机必须始终提供一部分能量给液力泵使用,增加了油耗;电机驱动的离合器执行机构工作时不需要发动机供能。

2)从控制的角度讲,液压作动离合器不易进行闭环控制,而是通过标定离合器结合不同阶段的油压实现开环控制,这是由于油压传感器的成本、安装和可靠性等原因造成的;而使用电机驱动方式,可以相对容易的控制离合器的结合过程,精度高,可靠性好。

Estop GmbH公司的Richard Roberts和Henry Hartmann曾于2002年设计出应用于汽车制动系统中的具有“自增力”效果的楔形机构[1],并且随后开发了该电控制动机构的控制技术。根据电控制动机构的设计思想,上海交通大学国家汽车工程研究院与北美通用汽车合作开发了一种伺服电机驱动的蜗轮蜗杆和楔形块的换挡离合器执行机构,如图1。目前,还没有任何其他研究机构或个人将楔形机构应用于自动变速器的离合器换挡执行过程中。

在自动变速器换挡过程中,离合器摩擦片之间滑磨产生很大的摩擦力矩,作用到换挡执行机构上,由于楔形块的本身的特点,可以将该摩擦力矩转换成有利于离合器摩擦片结合的力矩,配合蜗轮蜗杆机构的减速增扭效应,大大降低驱动电机的工作扭矩输出[3]。

然而,楔形机构也有不足之处,根据公式(1-1),换挡驱动力矩和执行力矩比值,即“自增力”特征系数为C*。理想状态下,当楔块的楔角的正切值等于摩擦片与楔块表面之间的摩擦系数的时候,特征系数为无穷大,即产生任意大小的换挡执行力矩,换挡输出力矩都为0。从控制理论的角度讲,此时该系统处于临界稳定状态,微小的扰动将会引起楔块位移的不确定变化;若楔角的正切值大于摩擦系数,C*为正值,此时输入稳定的正向驱动力矩可以输出稳定的执行力矩;若楔角正切值小于摩擦系数,C*为负值,电机需要提供负向的驱动扭矩防止楔块被“自增力”拉向离合器结合方向。

在摩擦片结合的过程中,摩擦系数随着温度的上升而增大,要维持稳定的换挡执行力矩,驱动力矩曲线会穿越特征系数的渐近线,意味着驱动力矩方向将发生变化,对驱动力的控制产生困难。如图1。

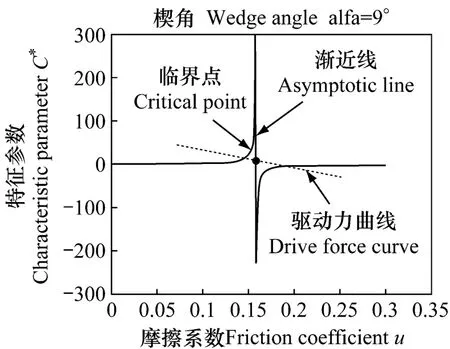
图1 Fig.1

鉴于以上分析结果,在进行机构设计时,需要优化楔角的大小,使得离合器结合过程中,既要保持一个较高的特征系数,又要防止驱动力方向发生变化,综合以上需求,本文介绍的离合器系统的楔角大约为 9°。

由于该机构接触件较多,接触件之间的碰撞和摩擦情况复杂,具有线性和非线性的元素,为了更清楚地分析和研究该执行机构的系统特性,本文利用Matlab-simulink对其进行数学建模,并对机械系统的关键参量,如惯量、阻尼、间隙等因素对系统响应的影响进行分析。

2 系统简介

如图2所示。在楔形离合器执行机构中,无刷直流电机通过联轴器与蜗杆轴相连,为机构提供驱动力,电机本身自带传动比为20的减速器,配合蜗轮蜗杆机构,带动楔形块运动,将转动转变成平动,从而提供足够的离合器结合压力。

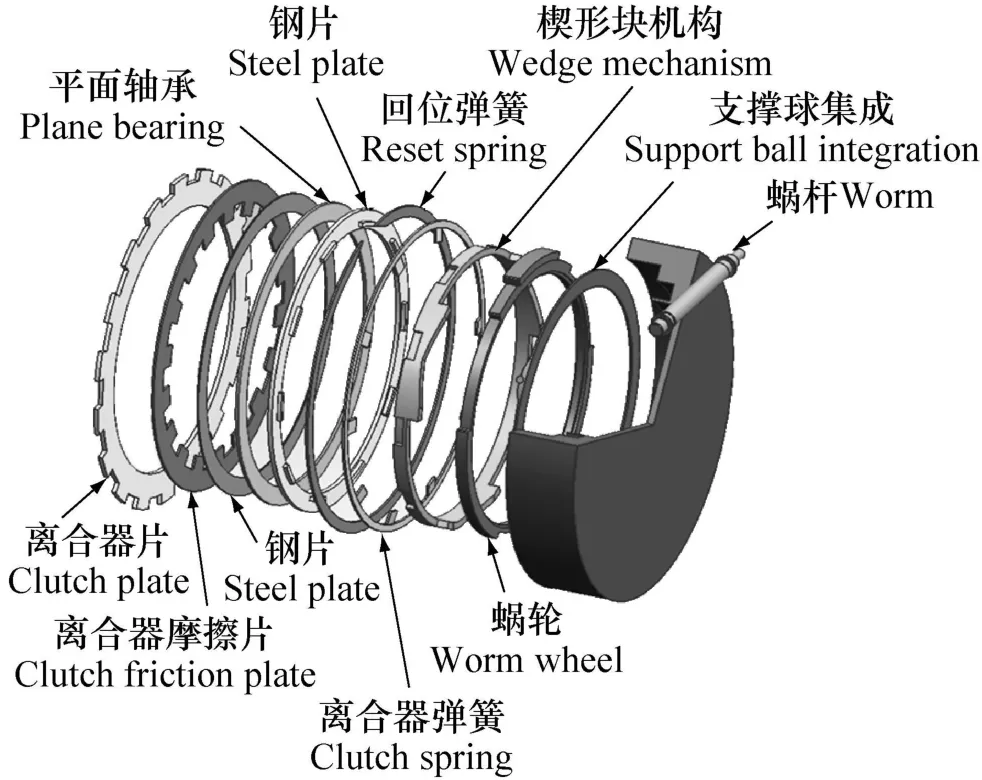
图2 楔形离合器机构三维模型图Fig.2 Wedge clutch mechanism 3D model diagram

离合器片固定于变速器箱体上,离合器摩擦片通过内花键套在行星轮上与其一同转动,电机提供使离合器结合的力矩的时候,蜗轮带动楔块机构转动,由于支撑球固定于箱体上,楔块机构也会产生沿变速器轴向的平动,进一步带动钢片将摩擦片压紧至离合器片,从而使得摩擦片停止转动,锁死响应的行星轮机构。

3 系统组件建模

为了建模分析方便,将楔形执行机构划分为如下几个模块：直流电机模块、蜗轮蜗杆机构模块、楔形机构模块和离合器摩擦片模块。

1)电机模块

电控楔形离合器机构的动力源是直流无刷电机,但是本文着重分析整个系统的响应,采用直流无刷电机模型显得过于复杂,会给后期的模型调试工作带来不必要的麻烦,所以本文使用简单的永磁直流电机模型[38]。

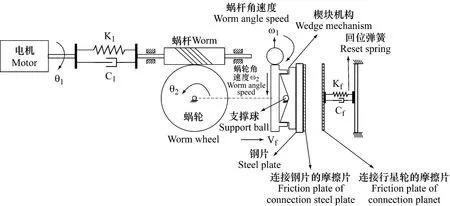
图3 电动楔形离合器系统示意图Fig.3 Electro wedege clutch system sketch

如图4为永磁直流电机模型示意图,根据直流电机的工作原理将该模块分为电磁线圈模型、机械模型和机电能量转化模型。

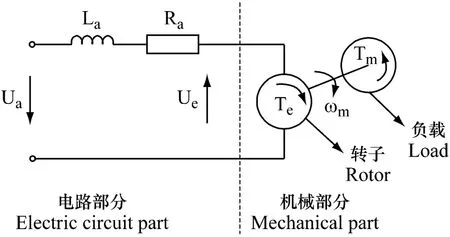
图4 直流电机原理图Fig.4 DC motor theory sketch

2)蜗轮蜗杆机构建模

该执行机构中,蜗轮蜗杆的具有将转动转化成平动的重要作用,其惯量和齿间摩擦对传动效率产生很大的影响,进一步影响到系统的响应,因此考虑以上两点因素,对蜗轮蜗杆机构进行建模如图5所示。

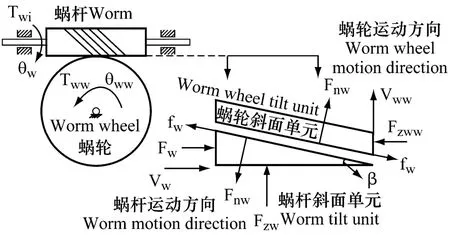
图5 蜗轮蜗杆原理图Fig.5 Worm and wheel theory sketch

蜗轮蜗杆接触点可以等效成为两个斜面单元的接触,对蜗杆斜面单元进行受力分析,得到公式(1),(2),(3)

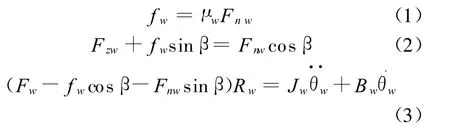
Rw是蜗杆的分度圆半径,Rww是蜗轮的分度圆半径,μw是蜗轮蜗杆齿间接触面的摩擦系数,Fw,Fww分别为作用于蜗杆和蜗轮上面的扭矩产生的对接触点斜面的作用力

对蜗轮斜面单元分析得到

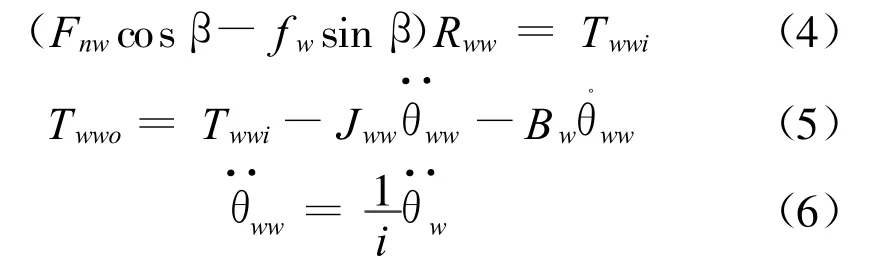
其中Twwi为蜗轮的输入力矩,即蜗杆对蜗轮产生的作用力矩,Twwo为蜗轮的输出力矩

综合以上各个等式可得：

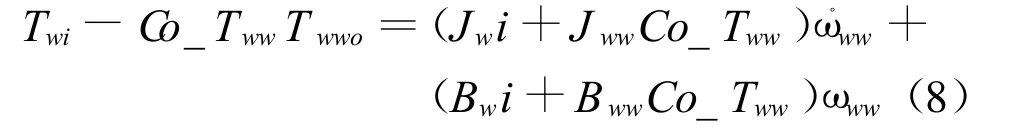
其中,Co_Tww为自定义系数

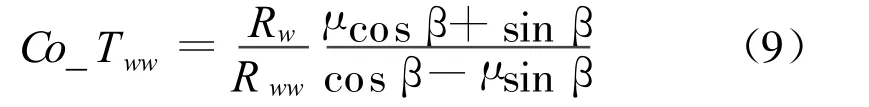
3)楔块机构建模

μ为楔块与摩擦片之间的摩擦系数,ωf,ωwe分别为摩擦片和楔块的角速度,Fb是楔块与摩擦片之间的动摩擦力

当 dwe≤dth时,楔块处于空行程阶段,对楔块进行受力分析得到公式

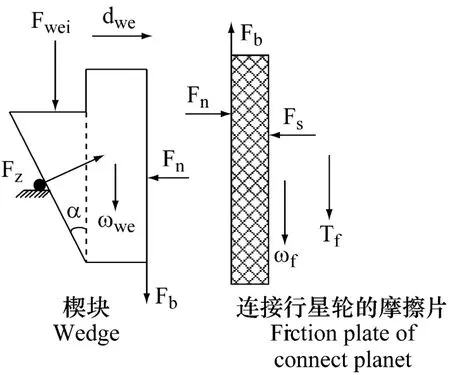
图6 (a)滑磨状态楔块受力模型Fig.6 (a)Slipping condition wedge forced model

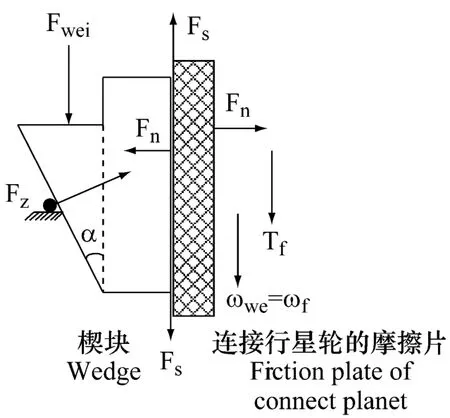
图6 (b)结合状态楔块受力模型Fig.6 (b)Engaged condition wedge forced model

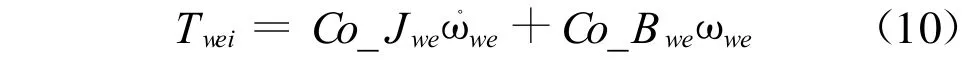
Co_Jwe=mweR2wetan2α+Jwe,为楔块环等效转动惯量,其中包含了平动惯量和转动惯量两个部分

B)当dwe＞dth,楔块和摩擦片之间进入滑磨阶段,若它们之间存在转差率,即 ωf-ωwe不为0,楔块受到来自摩擦片的正压力和摩擦力

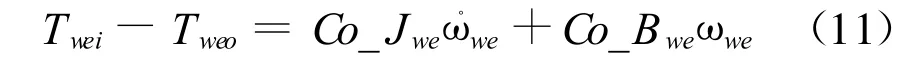
Tweo为阻碍楔块环转动的扭矩,包含了正压力和摩擦力在楔块转动方向上的作用,如公式12

C)当 dwe＞drh,但是 ωf-ωwe为 0,摩擦片通过花键套在行星轮上,当行星轮对摩擦片的扭矩Tf小于最大静摩擦扭矩Tsmax时,楔块与摩擦片处于结合阶段,且摩擦片锁死,楔块和摩擦片运动速度为0。

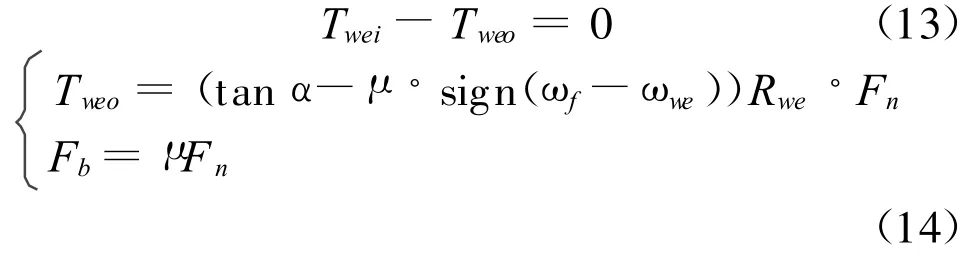
3 仿真结果与分析

摩擦片惯量Jf等于1.5 kg◦m3,摩擦片的阻力扭矩 Tf为0 Nm

为了分析楔形离合器系统各个元件惯量、阻尼等参数对离合器结合的响应过程,电机输入电压为18 V,

以下个图中,离合器状态的数值1,2,3分别代表离合器处于空行程,滑磨状态和结合状态,

图7中,对比了原始蜗轮惯量,10倍原始蜗轮惯量和50倍于原始蜗轮惯量三种不同参数下,对应的离合器状态变化以及摩擦片行程的变化。如图可知,当蜗轮惯量扩大50倍时,离合器要比原始蜗轮惯量下滞后进入滑磨状态大约80 ms;同样摩擦片也要滞后移动80 ms左右。

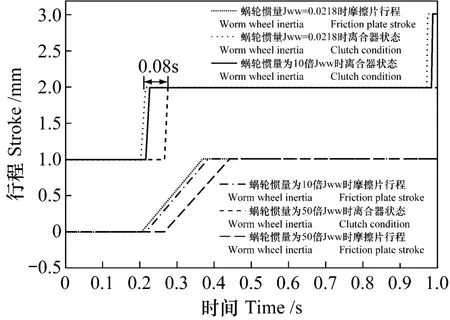
图7 蜗轮惯量对摩擦片行程及离合器状态的影响Fig.7 Worm wheel inertia effect on friction plate stroke and clutch condition

图8中,对比了原始蜗杆惯量,10倍原始蜗杆惯量和20倍于原始蜗杆惯量三种不同参数下,对应的离合器状态变化以及摩擦片行程的变化。如图可知,当蜗杆惯量扩大10倍时,离合器要比原始蜗轮惯量下滞后进入滑磨状态130 ms;当蜗杆惯量扩大20倍时,离合器比原始惯量情况下滞后进入滑磨状态220 ms;

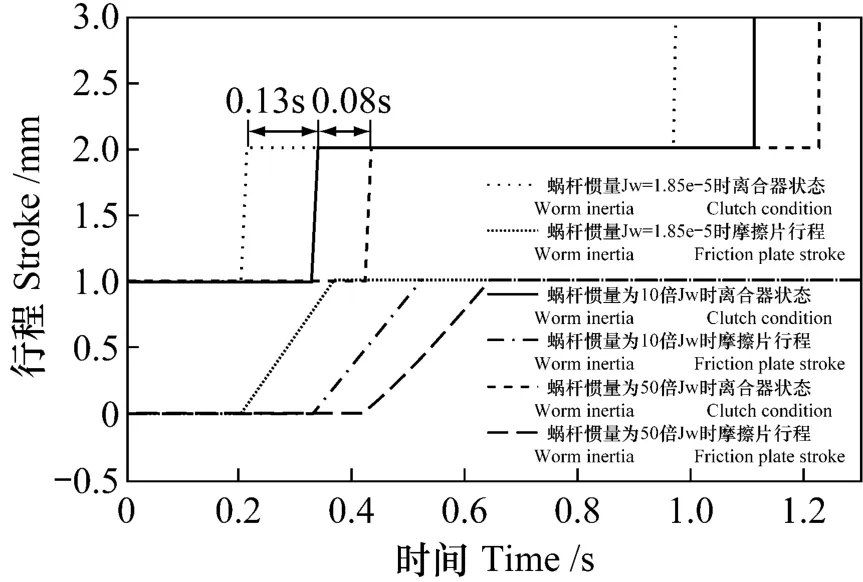
图8 蜗杆惯量对摩擦片行程及离合器状态的影响Fig.8 Worm inertia effect on friction plate stroke and clutch

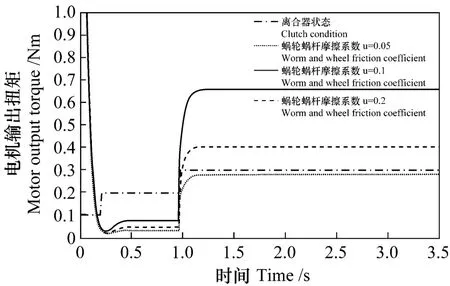
图9 蜗轮蜗杆齿间的摩擦系数对电机输出扭矩的影响Fig.9 Worm and wheel teeth friction coefficient effect on motor output torque

因为楔块的行程被限位在2 mm,楔块与离合器之间的空行程为1 mm,因此摩擦片弹簧压缩的最大位移是1 mm,当楔块推动摩擦片到达最大位移的时候,它们之间的正压力也达到最大值,为了维持系统平衡,电机输出扭矩。

4 结论

本论文介绍了一种伺服电机控制的楔形机构,对其进行分析,详细的阐述各个机构元件的物理学原理和它们之间的力作用关系,分别建立机构元件的动力学方程,在Matlab-simulink环境下进行仿真,得到楔形离合器系统在阶跃电压输入下的响应。本文还对比了在不同惯量、摩擦阻尼等条件下,系统阶跃响应的区别,找到对系统响应影响较大的因素,为优化机构设计提供了方便。

[1]Hartmann,Schautt,Pascucci&Gombert.“eBrake-the mechatronic wedge brake”.SAE Paper 2002-01-2582.

[2]Roberts,Schautt,Hartmann,&Gombert,“Modeling and Validation of the Mechatronic Wedge Brake”,SAE Paper 2003-01-3331.

[3]D.C.Karnopp,D.L.M argolis and R.C.Rosenberg,System Dynamics：Modeling and Simulation of Mechatronic System,John Wiley and Sons,Inc.New York,2000.