路轨两用消防车轨道行驶液压传动系统控制仿真研究
2011-07-06鲁统利
曹 阳 鲁统利
(上海交通大学汽车工程研究院,上海200240)
0 前言
随着经济的发展和城市的建设,地铁作为一种快速、环保、舒适、客运能力大的城市交通工具对于优化城市交通网络、缓解城市交通拥挤状况、振兴国家和地区的经济建设,起着非常重要的作用。为了有效地防范地铁灾害事故的发生和做好地铁火灾事故的灭火救援工作,有必要研制一种路轨两用特种消防车。该特种消防车底盘系统主要由公路行驶系统、轨道行驶系统、路轨转换系统三部分组成。公路行驶系统采用普通的机械传动,路轨转换系统、轨道行驶系统均采用液压传动控制技术,该车是一种复合型传动车辆。
该路轨两用消防车的轨道行驶驱动系统采用变量泵变量马达恒功率闭式液压系统,是一个典型的时变非线性系统,存在较大参数变化和大时变负载干扰。对一个结构确定而存在参数变化和干扰的液压驱动系统,需要一种随被控对象参数改变而自动变化的自适应控制方法。本文针对该路轨两用特种消防车的液压驱动模型,对其进行简化模型参考自适应控制算法的设计。仿真结果表明,以简化模型参考自适应控制策略具有控制精度高、响应快等特点,对特种消防车的轨道行驶速度控制具有良好的效果[1]。
1 路轨两用消防车液压驱动系统简化模型
路轨两用消防车的液压系统由闭式和开式两部分组成,前者为牵引传动系统,驱动车轮滚动;后者则是机构作动系统,操纵顶生油缸、锁止油缸、液压绞盘和冷却风扇。变速器后端有两个取力器,左边的用于闭式系统,而右边的则用于开式系统,轨道行走液压系统如图1所示。
路轨两用消防车的轨道行驶采用变量泵-变量马达系统,变量泵控制马达的原理如图2所示。变量泵阀控缸变量机构为一位置控制系统,开环传递函数为一积分环节加振荡环节组成的三阶系统,闭环传递函数则为惯性环节加振荡环节的三阶系统。考虑到目前的电液比例变量泵和马达均为机液力反馈位置闭环排量控制,其变量机构响应频率远高于系统频率,其排量与伺服控制器输出电流成比较准确的比例关系,伺服放大器频带更宽,同样为比例环节。本文为研究方便,将前述比例环节简化为常数。
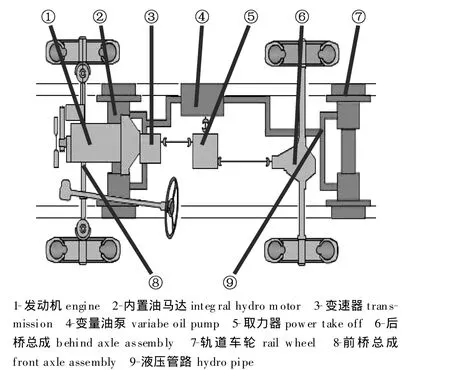
图1 轨道行走液压系统图Fig.1 Rail trak hydrautic system diagram
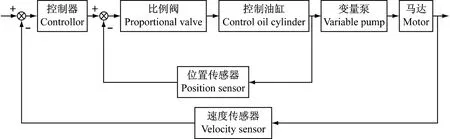
图2 变量泵控制马达的原理图Fig.2 Variable pump control motor theory diagram
忽略管路压力损失及动态;泵、马达泄漏为层流,泄漏系数与泄漏面两侧压差成正比;泵、马达的排量与其斜盘摆角成正比;闭式系统补油压力恒定;不计泵、马达摩擦转矩等非线性因素;负载和马达之间连接构件的刚度很大,可以忽略结构柔度的影响[2]。
(1)根据液体的流动性,得到泵与马达流量
连续方程:
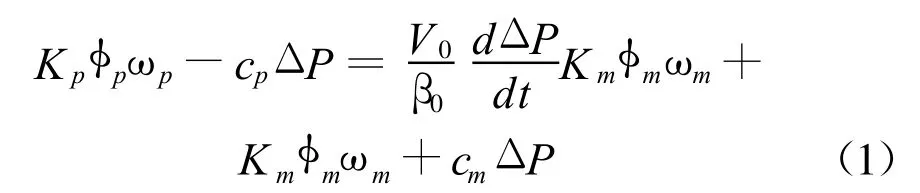
式中,Kp,Km为变量泵变量马达排量梯度;φp,φm为变量泵、变量马达的斜盘摆角;ωp,ωm分别为变量泵、马达的角速度;cp,cm分别为变量泵、马达的泄露系数;ΔP为泵、马达进出油口压差;V0为泵、马达、高压管端总容积;β0为油液容积弹性模数。
(2)液压马达力矩平衡方程为
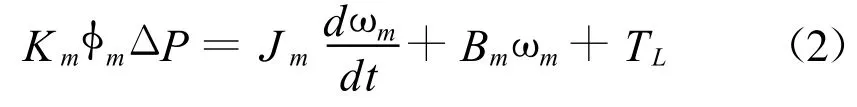
式中,Jm为等效至液压马达轴上的转动惯量;Bm为粘性阻尼系数;TL为负载扭矩。
将(1)、(2)两式进行拉氏变换,可得变量泵变量马达速度输出系统的传递函数为

式(3)中,
式(3)中变量马达斜盘摆角φm为一结构时变参数,随系统负荷压力的波动而变化,成为控制系统中的时变非线性因素。
2 模型参考自适应控制设计
在路轨消防车中,由于对系统的精度要求不是非常高,且系统的结构也相对简单,所以可以采用简化的模型参考自适应算法[2](SMARC),该方法与普通的模型参考自适应控制原理一致,原理如图3所示。(图中 ωm实际变量泵变量马达系统模型的输出,ωd为参考模型输出的期望值,e为参考模型的输出和实际被控系统的输出误差)。自适应机构根据误差e,经过自适应律的运算,产生调整作用,直接改变控制器参数,从而使实际变量泵变量马达系统的输出逐步与参考模型的输出接近,直到二者相等。只要选择综合性能很好的参考模型,这种简化模型参考的自适应算法的稳定性就能保证。
图3 模型参考自适应控制原理图Fig.3 SM ARC theory diagram
2.1 参考模型
参考模型[3]定义了期望的车辆动态响应。线性变量泵控定量马达速度输出系统最优二阶模型为
按时域优化设计方法,确定上式参数a3=(8/Th)3,a2=2(a3)1/3,a1=2(a3)2/3其中 Th为调整时间,由设计指标选择。
为了得到在稳定性、快速性和准确性方面均有优良性能的理想模型作为自适应控制的参考模型,对(5)式描述的二阶模型进行全状态反馈补偿校正,系统的反馈补偿校正方框图如图4所示。
图4 参考模型框图Fig.4 Reference model block diagram
2.2 自适应控制律
对于上面(3)和(6)描述的自适应方程,参考模型的状态空间表达式为
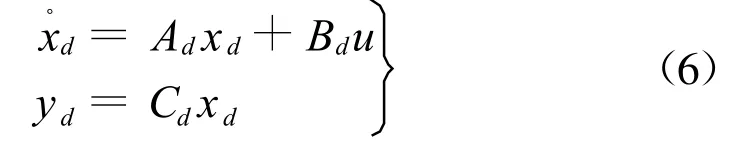
式中,
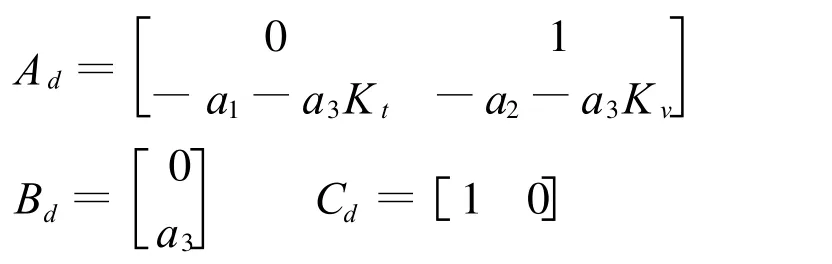
在此直接应用文献[4]给出了基于SMARC算法自适应控制规律,有:
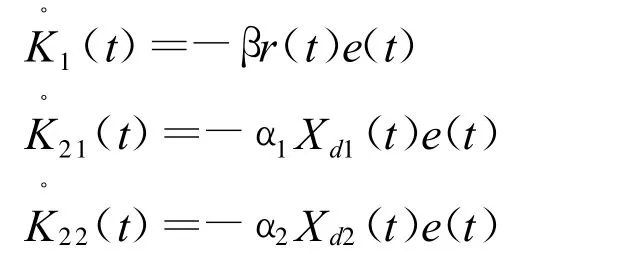
式中,α1,α2和β为自适应控制可调增益系数。可以看出该控制律为积分型控制律,其所调节的参数仅依赖于系统输入、参考模型状态及输出Y(t),对时变部分进行补偿,使e(t)趋于零。考虑到可调增益系数的不确定性,因而对实际系统辅以类是以参考模型的反馈校正。
3 仿真与分析
利用Matlab/Simulink对采用参考自适应控制策略对液压马达转速控制进行仿真,建立如图5所示的仿真模型。
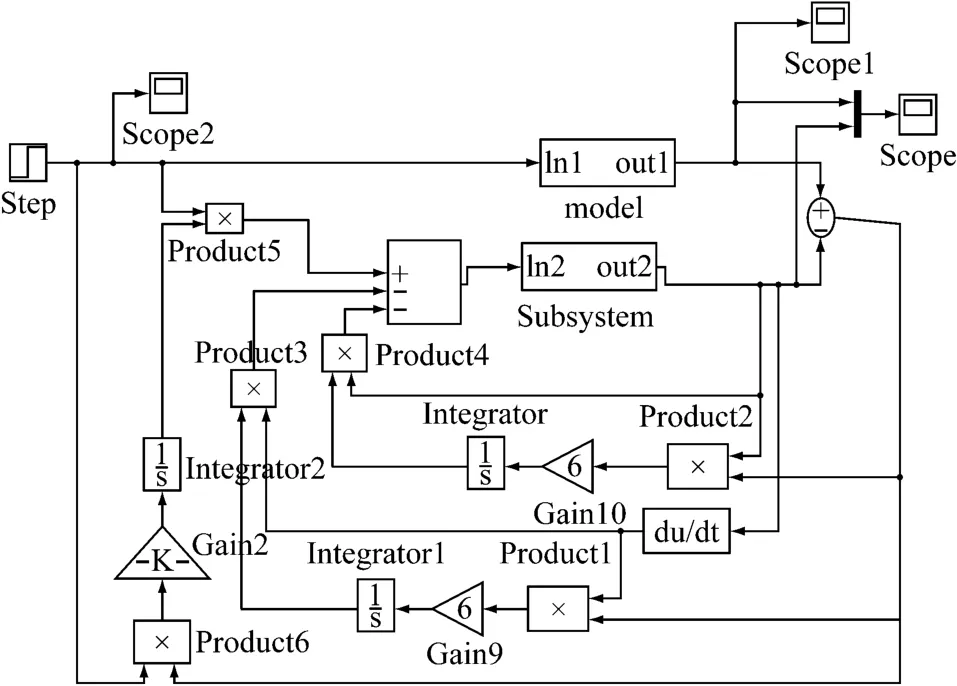
图5 简化模型参考自适应控制仿真Fig.5 SM ARC simalation
路轨两用消防车消防车液压驱动系统选择的SAUER公司90系列的变量泵和50系列的液压马达组成。主要仿真参数:
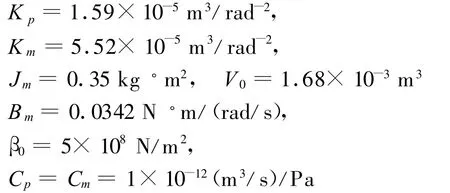
当马达不受外负载时,假设变量泵斜盘摆角为单位阶跃输入。图6所示为该输入下马达输出转速的动态响应特性曲线。由图可见,被控对象即液压马达趋于系统输入响应的调整时间较长,而自适应控制系统调整时间缩短,且过度过程平稳。仿真开始阶段自适应模型的输出误差较大,但随着误差的减小而稳定,能够较好的跟随参考模型的输出。
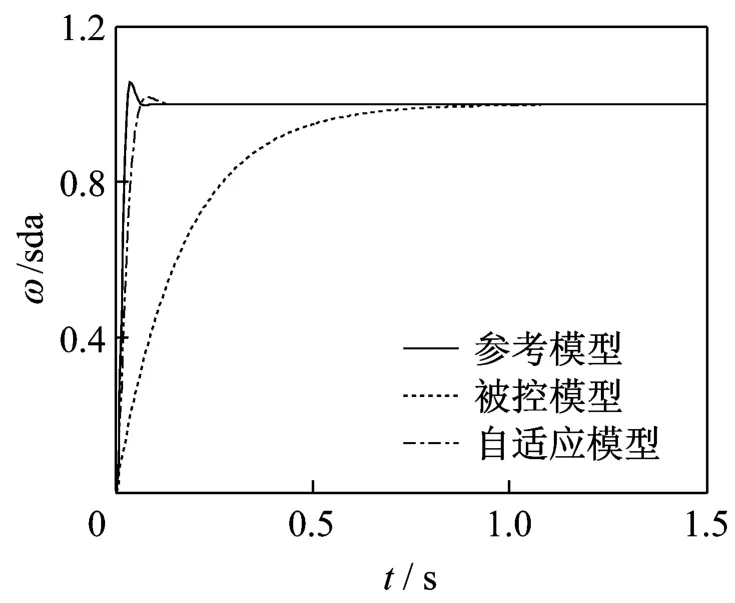
图6 阶跃输入下马达转速响应曲线Fig.6 Under step-input motor revolution response curve
当液压马达受外负载变量泵斜盘摆角为单位阶跃输入,1秒后给液压马达突加120 N◦m的阶跃外负载。图7所示为该输入下马达输出转速的动态响应特性曲线。由图可见,在负载干扰下,一开始被控系统输出影响较大,但随着自适应控制发挥作用,最终实现误差减小,稳定输出。
4 结论
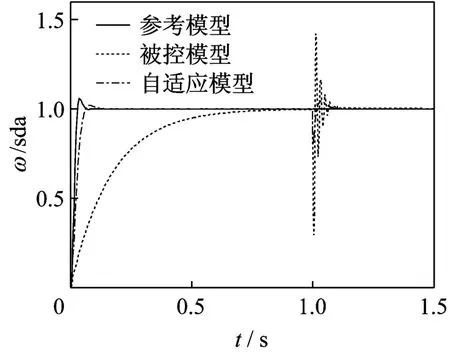
图7 阶跃负载下马达转速响应曲线Fig.7 Under step loading motor revolution response curre
针对变量泵变量马达闭式液压驱动系统的非线性特性,设计了以最优全状态反馈作为参考模型,运用了简化的模型参考自适应控制算法,并对其进行不同工况的仿真,获得较好的动态性能。仿真结果表明,该控制方法能够很好有效地克服变参数的影响,而且算法简单,能够应用在路轨两用消防车等工程机械上。
[1]王岩,付永领,刘建军.变量泵-变量马达自适应控制算法研究[J].中国机械工程,2009,20(10):1173-1179.
[2]姚怀新,陈超.工程机械驱动流量耦合系统自适应控制仿真[J].长安大学学报(自然科学版),2007,27(4):96-99.
[3]刘小河,崔杜武.非线性系统的模型参考自适应控制[J].西北大学学报(自然科学版),1994,29(2):99-103.
[4]刘峰.牵引车辆液压驱动系统自适应控制策略研究[D].西安,长安大学工程机械学院,2006.
