含不同半径孔洞的颗粒体模型的力学行为数值模拟

伍小林，王学滨，潘一山

（辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000）

0 引言

众所周知，试样的尺寸会影响其强度，甚至是峰后的应力-应变曲线。这种问题在固体力学和岩石力学中常称之为尺寸效应或尺度律问题。这些问题的重要性怎么强调也不过分，这是因为在很多的物理和工程问题中，尺度律问题都占据其中心位置［1］。目前，关于不含孔洞的矩形试样的尺寸效应问题研究得最为充分，尤其是单向压缩条件下岩石、混凝土等准脆性材料的尺寸效应问题［1-6］。

尺寸效应也存在于岩石钻孔的破裂之中［1］，这些现象的确认是通过室内试验得到的［7-8］。最近的现场观测表明，巷道断面的尺寸对岩爆的量级有重要的影响［9-10］。他们对某水电站探洞和交通洞开挖洞段的现场岩爆特征的调查统计表明，岩爆的基本地质条件基本相同，但是，在探洞（断面为3m×3m）发生了II级岩爆（比I级岩爆弱），而交通洞（断面为6m×6m）发生了I级岩爆，并由此推测，岩爆量级随断面开挖尺寸的增大而增强，岩爆具有尺寸效应。文献［11］开展了不同尺寸的隧洞开挖之后，围岩的剪切局部化过程的数值模拟研究。在计算中，采用了FLAC软件的应变软化本构模型，以“先加载，后挖洞”方式进行模拟。研究结果表明，对于小孔隧洞，围岩中出现了4个对称的V形坑，这与静水压力条件下有关的实验结果和现场观测结果较为吻合；对于大孔隧洞，围岩中出现了多条狭长的剪切带，围岩发生了大面积的破坏。由此发现了隧洞的尺寸对围岩的局部化有重要的影响。

本文将岩石视为非连续介质，即由颗粒和界面构成的颗粒体材料，采用FLAC对含不同半径孔洞的颗粒体模型进行了数值模拟。在静水压力条件下，先将模型加载至平衡，然后再通过 FLAC的内嵌编程FISH语言模拟开挖。研究了模型再次平衡后，巷道半径不同时，围岩中的剪切应变增量、最小主应力及最大主应力的分布规律，此外，还监测了一些单元的一些力学量的分布规律，进一步确认了巷道的尺寸对围岩变形破坏的重大影响。

1 颗粒的堆积算法

颗粒的堆积过程是在某一矩形区域内由下至上进行的。为了易于实现颗粒堆积算法，需要事先在矩形区域下边界上人为地放置一排颗粒。矩形区域的左边界和右边界均可视为半径为无限大的颗粒。在本文中，表层颗粒是指众多颗粒堆积成的堆积体的表面一层的颗粒。表层颗粒中的任一颗粒均未被其周围的颗粒完全包围，即颗粒的上方无任何颗粒而其下方至少有两个颗粒与之相切。颗粒的堆积算法如下：

（1）记录当前表层颗粒，即矩形区域下边界上的一排颗粒。

（2）假设颗粒半径服从均匀分布，随机产生一个半径为rn的新颗粒n。

（3）在表层颗粒中随机抽取一个颗粒i。

（4）在颗粒i附近找到一个颗粒j（颗粒j可为左边界、右边界或表层颗粒），使得新颗粒n能放在颗粒i和j之上，并且与颗粒i和j都相切。

（5）根据几何关系求出新颗粒n的中心坐标，设其中心坐标为（xn，yn）。由颗粒i和颗粒n相切的关系，可得：

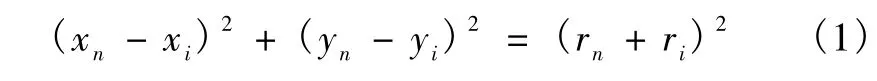
式中：ri——颗粒i的半径；

xi，yi——颗粒 i的中心坐标。

如果颗粒j与新颗粒n相切，那么将可能出现三种情况：

a）若颗粒j为左边界，则有

b）若颗粒j为右边界，则有

式中a为矩形区域水平方向的长度。

c）若颗粒j为表层颗粒，则有

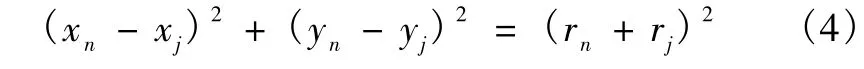
式中：rj——颗粒j的半径；

xj，yj——为颗粒 j的中心坐标。

由式（1）与式（2）、（3）及（4）中的任一个可求出新颗粒n的中心坐标（xn，yn）的两组解：其中一组 yn值较小的解对应于新颗粒n在颗粒i和j下方的情况，因而应当舍去；另一组解即为所求。

（6）判断新颗粒n的中心横坐标xn是否介于颗粒i的中心横坐标xi与颗粒j的中心横坐标xj（或左边界、右边界）之间，以确保新颗粒n在重力作用下能保持静止。若xn不介于它们之间，则再回到第（3）步；否则，进行下一步。

（7）本文不允许两个颗粒相互侵入，因此需要判断任意两个颗粒是否相互侵入。只要有一个颗粒与新颗粒相互侵入，则再回到第（3）步；否则，进行下一步。

（8）修改当前表层颗粒的记录。

（9）重复（2）到（8）步，直至结束。

图1给出了利用上述算法获得的颗粒的堆积过程。

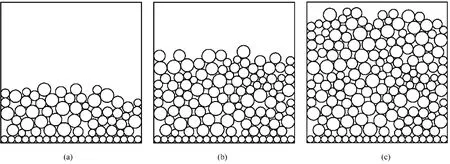
图1 颗粒堆积过程Fig.1 The accumulating process of granulaes

2 计算模型、计算方案及本构关系

按上述算法在某一矩形区域内生成颗粒堆积体，再从中切割出一个边长为1m的正方形试样，试样的详细切割过程见文献［12］。试样内的颗粒数目为2795，颗粒的最小半径为 0.00625m，最大半径为0.0125m。为了模拟颗粒之间的接触和滑动，在任意两个相互接触的颗粒之间规定了界面。在本文中，将颗粒和界面都离散为正方形单元构成的集合体。图2中深灰色的单元为界面单元，而浅灰色的单元为颗粒单元。若包括孔隙在内，则本文模型中有500×500个单元。模型中颗粒和界面单元总数分别为174937及29353。由此可以计算出孔隙度约为（500×500-174937-29353）/（500×500）=0.183。

采用了5个计算方案。方案1至5的模型的中心孔洞半径R不同，其它参数均相同。方案1至5的R分别为0.075m、0.125m、0.175m、0.225m 及 0.275m。模型四周的水平和垂直方向所施加的压应力均为3MPa。监测了方案1和5中一行单元的剪切应变增量、最大主应力及最小主应力的分布规律。这一行单元是通过巷道中心的水平线上的单元，且位于巷道的左侧。图2（a）中的拟开挖的巷道与监测单元的位置是以方案5为例，各方案中的巷道半径和监测单元的数量有所不同。

计算步骤如下：首先，在给定的本构关系、边界条件及加载条件下，对未开挖的模型进行计算，阻尼由FLAC自行施加，直至达到静力平衡状态。在本文中，当最大失衡力小于0.05N时，停止计算。此时，认为模型已经达到了静力平衡状态。然后，利用编写的FISH函数［13］删除孔洞内的单元，即开挖巷道。由于开挖卸荷产生了失衡力，因此模型不再处于平衡状态。最后，对开挖后的模型进行计算，阻尼由 FLAC自行施加，一直计算到4万步为止。从失衡力-时步曲线可以发现，此时，各方案均达到了静力平衡状态。本文仅给出了此时的计算结果。

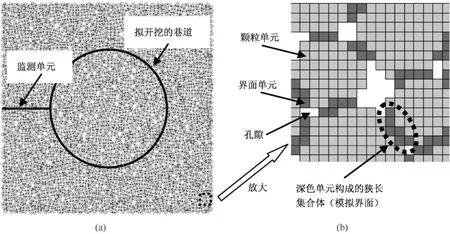
图2 颗粒堆积体模型（a）及局部放大图（b），图2（a）中的巷道尺寸及监测单元是以方案5为例Fig.2 The model of granular material（a）and a close-up figure（b），where the tunnel size and the position of monitored elements are for Scenario 5

在本文中，颗粒体被视为各向同性的弹性材料，界面在破坏之前也被视为各向同性的弹性材料，而界面在破坏之后被视为莫尔-库仑材料。弹性模量取为26.52GPa，泊松比取为0.21，内聚力取为2MPa，内摩擦角取为30°，抗拉强度取为1MPa。

3 结果分析及讨论

3.1 剪切应变增量的分布规律

图3给出了方案1至5的剪切应变增量高值区分布的等值线图。图3中的黑色区域为剪切应变增量的高值区。为使剪切应变增量的分布显示得更清晰，图3（a-e）中均未显示大于3×10-4的剪切应变增量。由图3可以发现，剪切应变增量的高值区主要位于巷道表面附近，且呈圆环形分布。在方案1至5中，圆环的圈数大致分别为1、2、3、5及8。由此可以发现，圆环的圈数随孔洞半径的增大而呈先慢后快的增长趋势。计算表明，方案1至5的剪切应变增量的最大 值 分 别 为 0.8466 ×10-3、1.3461 ×10-3、1.8376 ×10-3、3.0219 ×10-3及 5.4776 ×10-3。由此可以发现，剪切应变增量的最大值随孔洞半径的增大而先慢后快地增大。这些剪切应变增量的最大值均出现在巷道表面附近。图4给出了方案1至5的剪切应变增量的最大值位置的局部放大图。在图4中，颜色越深表示剪切应变增量的值越高，可以发现，剪切应变增量的最大值位置的单元（箭头所指单元）发生了较为明显的剪切变形。为什么是巷道表面附近的这些位置的单元具有最高的剪切应变增量？或许是由于这些单元附近有较大的孔隙且它们周围的颗粒较为稀疏所致，因此这些单元易发生剪切错动而产生较高的剪切应变增量。

图5给出了方案1和5中监测单元的剪切应变增量的分布规律。监测的单元被重新进行了编号，第一个单元为离模型左边界最近的单元，图5中的横坐标表示单元编号（不包括孔隙在内）。由图5可以发现，剪切应变增量的分布曲线具有多个峰。方案1和5中巷道左侧一定范围内的单元的剪切应变增量的值都较高。方案5的剪切应变增量的值及高值区的范围都远大于方案 1。此外，还可以发现，方案 1和5中峰的个数分别与图3（a）和（e）中圆环的圈数大致相同。

图3 不同方案的剪切应变增量分布Fig.3 Shear strain increment distribution in different scenarios

图4 不同方案的剪切应变增量的最大值位置的局部放大图Fig.4 C lose-up figures of the position with maxim um shear strain increment in different scenarios

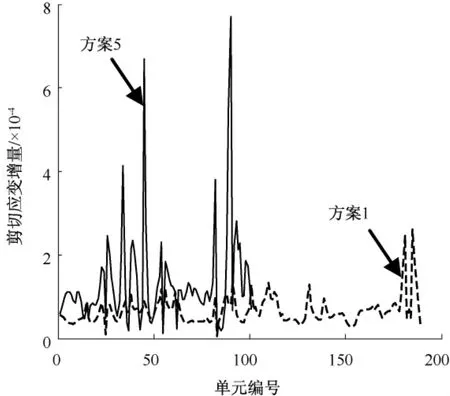
图5 方案1和5的监测单元剪切应变增量分布Fig.5 Shear strain increment distributions of monitored elements in scenarios 1 and 5

3.2 最小主应力的分布规律

图6给出了各方案的最小主应力的高值区分布的等值线图。为了清晰地显示最小主应力的分布规律，图6（a-e）中只显示了-10MPa至0之间的最小主应力。FLAC中的最小主应力一般为负值，代表很高的压应力。在图6中，颜色越深表示压应力的值越大。图6与图3中剪切应变增量高值区的分布规律较为类似。计算表明，方案1至5的最小主应力的最小值（即最大的 压 应 力）分 别 为 -15.798MPa、-21.916MPa、-18.787MPa、-28.950MPa及 -28.443MPa。由此可以发现，各方案的最大的压应力约为模型四周所施加的压应力（3MPa）的5～10倍。

图7给出了方案1和5中监测单元的最小主应力的分布规律。由图7可以发现，最小主应力的分布曲线也出现了多个峰。方案1和5中巷道左侧一定范围内的单元的最小主应力的值（压应力）都较大，而方案5的最小主应力的值及高值区的范围都远大于方案1。此外，图7中具有较大的压应力（绝对值大的负值）的位置大部分都与图5中剪切应变增量的峰的位置相同。

3.3 最大主应力的分布规律

图6 不同方案的最小主应力分布Fig.6 Minim um principle stress distribution in different scenarios

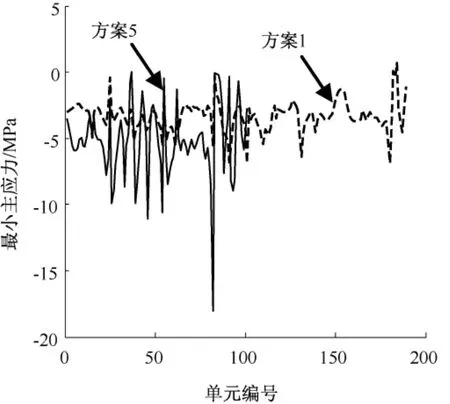
图7 方案1和5的监测单元的最小主应力的分布Fig.7 Minim um principle stress distributions of monitored elem en ts in scenarios 1 and 5

图8给出了不同方案的最大主应力的高值区分布的等值线图。在图8中，为了更清晰地显示最大主应力的分布规律，只显示了0至3MPa之间的最大主基本上等于或大于模型四周所施加的压应力（3MPa）。应力。图8中的黑色区域为最大主应力的高值区。FLAC中的最大主应力通常为正值，表示较高的拉应力。由图8（a-e）可以发现，最大主应力呈辐射状分布，且随着孔洞半径的增大，最大主应力的高值区由巷道表面附近逐渐延伸到围岩内部。方案1至5中最大主应力的高值区延伸的长度分别约为15、28、42、60及79个单元。由此可以发现，最大主应力的高值区延伸的长度也随孔洞半径的增大而呈先慢后快的增长趋势。由图8及图3可以发现，各方案中最大主应力的高值区延伸的长度与剪切应变增量的高值区分布的范围大致相同。计算表明，方案1至5的最大主应力的最大值（最大的拉应力）分别为2.841MPa、 3.233MPa、 3.541MPa、 4.536MPa 及4.339MPa。由此可以发现，各方案的最大的拉应力

图8 不同方案的最大主应力分布Fig.8 Maxim um principle stress distribution in different scenarios

图9给出了方案1和5中监测单元的最大主应力的分布规律。由图9可以发现，最大主应力的分布曲线也具有多个峰。方案1和5中巷道左侧一定范围内的单元的最大主应力的值（拉应力）都较大，而方案5的最大主应力的值及高值区的范围都远大于方案1。两个方案中高值区的范围分别与图8（a）和（e）中拉应力的延伸的长度大致相同。为了揭示剪切应变增量与差应力（最大主应力与最小主应力之差）之间的关系，图10同时给出了方案5中监测单元的剪切应变增量与差应力的分布规律。可以发现，二者的峰值的位置基本相同。因而，具有较高的差应力的位置，也具有较高的剪切应变增量。

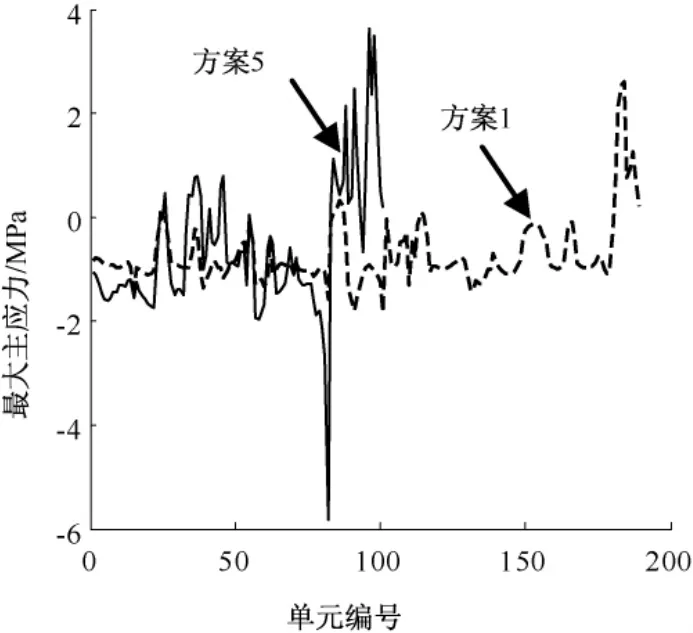
图9 方案1和5的监测单元的最大主应力的分布Fig.9 Maxim um principle stress distributios of monitored elements in scenarios 1 and 5

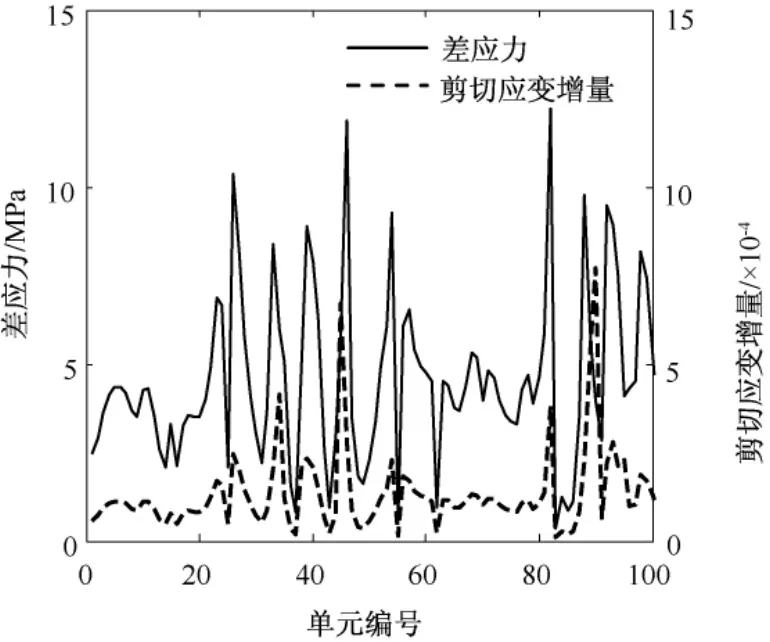
图10 方案5的监测单元的差应力与剪切应变增量的分布Fig.10 The distributions of the shear strain increm ent and the differential stress of monitored elem ents in scenario 5

3.4 简短的讨论

对于 Berea砂岩，其孔隙度在 17％ ～25％［14］，本文模型的孔隙度为18.3％，与其下限更接近。通常，砂岩的平均颗粒半径越大，则孔隙度越大。当砂岩的孔隙度为25％时，其平均颗粒半径可以达到0.25mm［14］，而 在 本 文 中，颗 粒 的 平 均 半 径 为0.009375m，将近1cm。因此，这是颗粒实际尺寸的40倍以上。不仅本文作者，其他作者在研究尺度稍大的问题中，颗粒尺寸的选取都普遍高于颗粒的真实尺寸。例如，文献［15］中颗粒半径为 0.2m；文献［16］中颗粒半径为0.01m，这与本文接近；文献［17］中颗粒半径约为1.5cm。和上述三篇文献相比，本文中颗粒的尺寸是最小的。限于本文作者所使用的微机的硬件水平，目前还无法在1m×1m的模型中，考虑颗粒的真实尺寸。尽管如此，并不妨碍对洞室尺寸效应问题的理解，这是本文工作的重点。

洞室尺寸效应问题的研究，在大规模岩石工程不断向深部发展，以及需要越来越大的地下洞室被开挖的今天，显得愈加重要和紧迫。在高地应力条件下开挖大断面的地下洞室时，如果仅在设计阶段基于均匀、连续介质力学方法进行分析和计算，可能会低估岩石工程建设及运行阶段发生岩爆等地质灾害的风险。因此，应该寻找更加行之有效的研究手段和技术，岩石的细观结构不应该被忽视。

4 结论

（1）剪切应变增量与最小主应力的高值区（压应力区）都呈圆环形，主要分布于巷道表面附近，且随着孔洞半径的增大，圆环的圈数及剪切应变增量的最大值都呈先慢后快的增长趋势。最大主应力的高值区（拉应力区）呈辐射状，其延伸范围随着孔洞半径的增大，也呈先慢后快的增长趋势。模型中最大的拉应力接近于模型边界上所施加的压应力，而最大的压应力约为所施加的压应力的5～10倍。

（2）巷道左侧围岩中监测单元的剪切应变增量、最小主应力及最大主应力的分布曲线都具有多个峰，这表明它们的分布是高度不均匀的。在巷道表面附近，如果有些位置的单元周围的孔隙较大且颗粒较为稀疏，则这些单元可能更易发生剪切变形而产生较高的剪切应变增量。具有较高的差应力的位置与具有较高的剪切应变增量的位置具有很好的一致性。

［1］BaŽant Z P，Chen E P.结构破坏的尺度律［J］.力学进展，1999，29（3）：383-433.BaŽant Z P，Chen E P.Scaling of structural failure［J］.Advances in Mechanics，1999，29（3）：383-433.

［2］Hudson J A，Crouch S L，Fairhurst C.Soft，stiff and servo-controlled testing machine：a review with reference to rock failure［J］.Eng Geol，1972，6（3）：155-189.

［3］Jansen D C，Shah S P.Effect of length on compressive strain softening of concrete［J］.J Eng Mech，ASCE，1997，123（1）：25-35.

［4］Van Mier J G M，Shah S P，Arnaud M，et al.Strain-softening of concrete in uniaxial compression-report of the round robin test carried out by RILEM TC 148-SSC［J］.Mat Struct，1997，30（198）：195-209.

［5］王学滨，潘一山，宋维源.岩石试件尺寸效应的塑性剪切应变梯度模型［J］.岩土工程学报，2001，23（6）：711-714.WANG Xuebin， PAN Yishan， SONG Weiyuan.The model of plastic shear strain gradient on size effect in uniaxial compression of rock specimen［J］.Chinese Journal of Geotechnical Engineering，2001，23（6）：711-713.

［6］WANG X B.Prediction of height effect， plastic deformation and fracture energy for high-strength concrete by linear shear softening constitutive relation based on energy conservation method［J］.Magazine of Concrete Research，2007，59（5）：341-350.

［7］Carter B C.Size and stress gradient effects on fracture around cavities［J］.Rock Mech and Rock Eng，1992，25（3）：167-186.

［8］Carter B C，Lajtai E Z，Yuan Y.Tensile fracture from circular cavities loaded in compression［J］.Int J Fracture，1992，57：211-236.

［9］孟陆波，赵建壮.岩爆的洞室效应［J］.中国地质灾害与防治学报，2008，19（2）：59-62.MENG Lubo，ZHAO Jianzhuang.The chamber effects of rock burst［J］.The Chinese Journal of Geological Hazard and Control，2008，19（2）：59-62.

［10］孟陆波，李天斌，周春宏，等.某水电站洞室岩爆的尺寸效应［J］.水力发电，2008，34（1）：29-31.MENG Lubo，LITianbin，ZHOU Chunhong，et al.Rock burst′s dimensional effect on the tunnels of a hydropower station［J］.Water Power，2008，34（1）：29-31.

［11］王学滨，潘一山，陶帅.不同尺寸的圆形隧洞剪切应变局部化过程模拟［J］.中国地质灾害与防治学报，2009，20（4）：101-108.WANG Xuebin，PAN Yishan，TAO Shuai.Numerical simulation of shear strain localization processes along circular tunnels with different diameters［J］.The Chinese Journal of Geological Hazard and Control，2009，20（4）：101-108.

［12］伍小林，王学滨，潘一山.单向压缩条件下圆形颗粒体含孔洞试样的力学模拟［J］.水利水运工程学报，2010，（3）：40-44.WU Xiaolin，WANG Xuebin，PAN Yishan.Numerical simulation of mechanical behavior of a specimen composed of circular granular material［J］.Hydro-Science and Engineering，2010，（3）：40-44.

［13］王学滨，王玮，潘一山.孔隙压力条件下圆形巷道围岩的应变局部化数值模拟［J］.煤炭学报，2010，35（5）：723-728.WANG Xuebin，WANG Wei，PAN Yishan.Numerical simulation of the strain localization of the surrounding rock of a circular tunnel at different pore pressures［J］.Journal of China Coal Society，2010，35（5）：723-728.

［14］Haimson B C.Borehole breakouts in berea sandstone reveal a new fracture mechanism［J］.Pure and Applied Geophysics，2003，160：813-831.

［15］王涛，吕庆，李杨，等.颗粒离散元方法中接触模型的开发［J］.岩石力学与工程学报，2009，28（增2）：4040-4045.WANG Tao，LU Qing，LI Yang，et al.Development of contact model in particle discrete element method［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28（Supp.2）：4040-4045.

［16］周健，邓益兵，贾敏才，等.基于颗粒单元接触的二维离散 -连续耦合分析方法［J］.岩土工程学报，2010，32（10）：1479-1484.ZHOU Jian，DENG Yibing，JIA Mincai，et al.Coupling method of two-dimensional discontinuum -continuum based on contact between particle and element［J］.Chinese Journal of Geotechnical Engineering，2010，32（10）：1479-1484.

［17］Hazzard J F， Young R P.Moment tensors and m icromechanical models［J］.Tectonophysics， 2002，356：181-197.