邻近既有线深基坑开挖过程中的动力响应分析

李梅芳，肖军华，宫全美，周顺华

（同济大学道路与交通工程重点实验室，上海201804）

随着全国铁路网的不断扩大，客运专线的大规模开工建设，大部分既有车站需要在维持既有线路运营的情况下进行改扩建，在这些工程中不可避免地存在既有线列车荷载作用下基坑与线路之间的相互影响的问题:一方面新建车站基坑开挖会影响既有线结构变形，从而引起既有线轨道变形，影响行车安全；另一方面轮轨动荷载引起的基坑结构变形也可能会影响基坑的稳定性和安全性，因此对这个问题开展研究十分必要。

国内学者针对深基坑开挖及既有线路上的动力响应分析做了大量的研究。王卫东[1]等对上海地区预估深基坑开挖对周边建筑物影响的简化分析方法进行了研究。然而，简化分析方法一般根据工程人员的经验进行算法与参数的选取，且无法考虑既有线路上列车动荷载的作用；张晨明等[2]针对新线施工对既有线车站的影响进行了研究，得到不同施工步下既有结构的隆起量，但并未考虑列车荷载的动态作用。罗锟等[3]对沪宁城际铁路基坑开挖对既有线的动态影响进行了研究，分析了3种不同基坑支护方式下既有线路基的动态沉降值。毕湘利等[4]对列车振动邻近深基坑的既有站变形进行了研究，主要分析了换乘站基坑开挖过程中，列车动荷载引起的既有车站结构位移变化。但两者均未对既有线列车荷载作用下基坑与线路之间的动态相互影响作用进行分析。国内外学者虽然对深基坑开挖及列车振动荷载下结构的响应已经进行了一定的研究，但是由于既有线列车荷载作用与邻近的基坑开挖过程的相互影响是一个受力、变形机理复杂的问题，目前尚未形成一套较合适的分析理论。因此对邻近既有线深基坑开挖过程中的动力响应研究还有待进一步的深入，以在保证在类似工程施工过程中既有线路及基坑结构的稳定性。

本文利用有限元数值分析软件，建立铁路路基－土体－邻近线路基坑－支护结构计算模型，对邻近既有线深基坑开挖过程中，列车振动荷载作用下路基－基坑体系的动力响应情况进行分析。由于邻近铁路的深基坑施工是按照严格的变形控制要求进行的，结构和周围土层的变形均属于小变形的范畴，本文将轮轨接触荷载对路基和周围环境的影响单独考虑，分析不同开挖步骤下邻近基坑的铁路运营线路在列车动载下的变形稳定性以及深基坑周围土体的动力响应情况。

1 工程概况

苏州火车站深基坑长56 m，宽34.1 m，开挖深度17.4 m，基坑采用两级1∶1放坡开挖，其中一级边坡高3.85 m，二级边坡高4.2 m，两级边坡中间设2 m宽平台。基坑开挖施工支护方案为:上、下级边坡均采用Ф16锚杆支护，上边坡锚杆长3.5 m，下边坡锚杆长6.5 m，纵横向间距均为1.5 m；两级边坡平台下设两排Ф850 mm，间距600 mm水泥搅拌桩，桩长10 m；基坑南、北侧围护结构均为地下连续墙，墙厚1 000 mm，入土深度分别为18.7 m，20.2 m；坑底以下采用旋喷桩裙边加固，加固宽度4 000 mm，深度3 000 mm。坑内布置3道支撑:第1道为混凝土支撑，截面高1 000 mm，宽800 mm，纵向间距7.0 m；第2，3道均为钢支撑，截面尺寸Ф609 mm、t=16mm，纵向间距2.5 m。距基坑南侧地下连续墙外边缘16.8 m处有一既有铁路站线，基坑第一层放坡开挖坡顶距既有线中心8.25 m，基坑及周边环境剖面如图1所示。基坑施工范围内各土层的物理力学指标如表1所示。

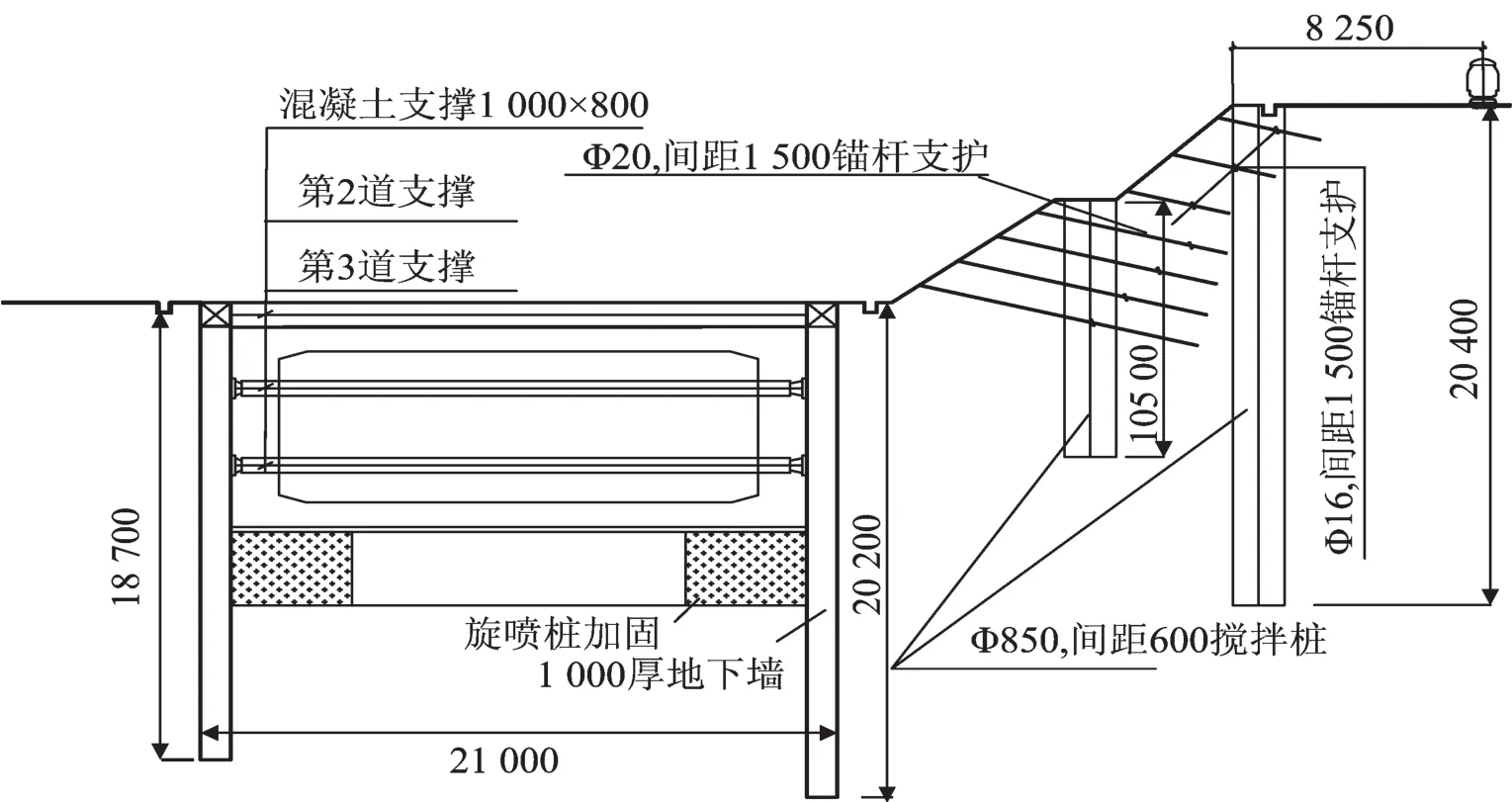
图1 基坑剖面图（单位:mm）Fig.1 Section of the foundation pit（Unit:mm）

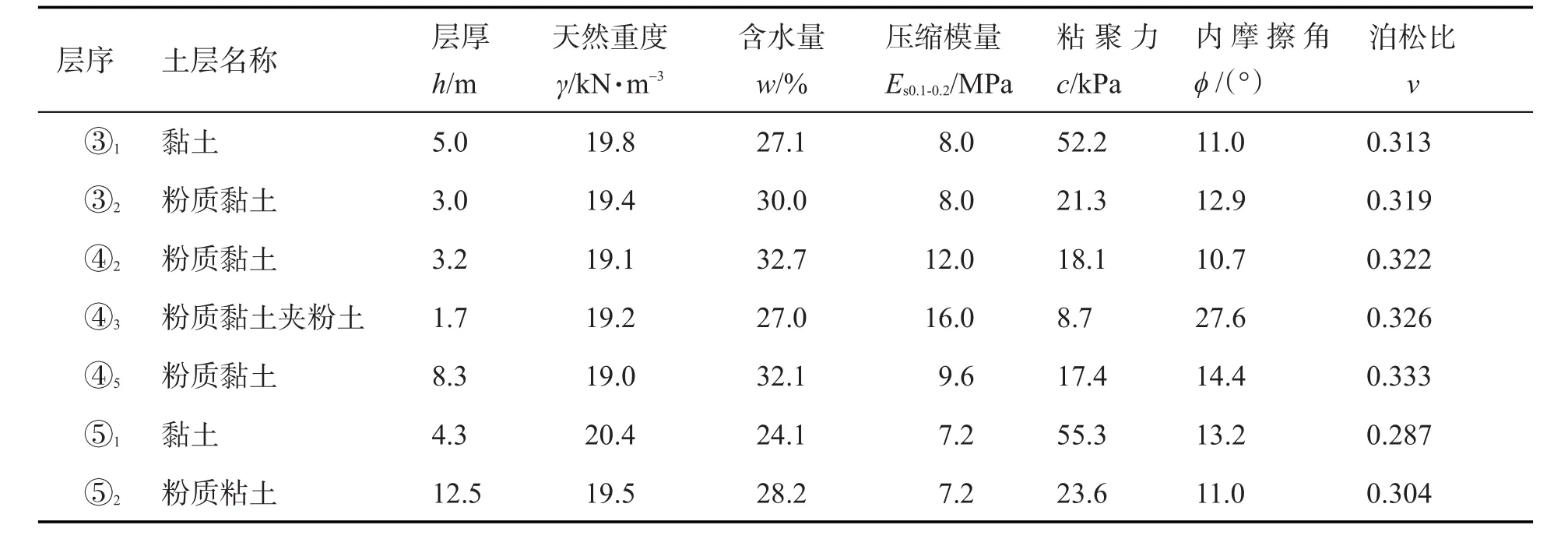
表1 主要土层的物理力学指标Tab.1 Mechanical parameters of soil

2 计算理论

本文采用有限元数值分析方法模拟地铁列车振动荷载作用下路基－土体－基坑－支护结构体系的相互作用问题。计算时假定[5]:1沿列车行驶方向，各断面结构及承受荷载情况基本一致。因此，可以将实际的三维问题简化为二维平面应变问题进行分析，简化计算；2动力荷载作用下各层土之间、土体－基坑结构之间不发生脱离和相对滑动；3将基坑周围的土体看作是各向同性的均质弹塑性体。由于邻近基坑的既有线为站线，本文采用列车通过速度45 km·h-1（侧向过岔速度）[6]的计算所得振动荷载。列车荷载作用在路基表面上力[7]的时程曲线如图2所示。

受计算速度和计算空间限制，所选取的有限元计算区域为95 m×40 m。将上部地表面设为自由边界，计算区域的底部边界在2个方向上均为固定约束，左右边界允许产生竖向位移而无水平向位移。对土体采用Mohr-Coulomb屈服准则，用平面4节点等参单元模拟；将钢筋混凝土及水泥搅拌桩结构视为弹性体，用平面4节点等参单元模拟；锚杆采用2节点杆单元模拟；混凝土支撑采用2节点梁单元模拟。

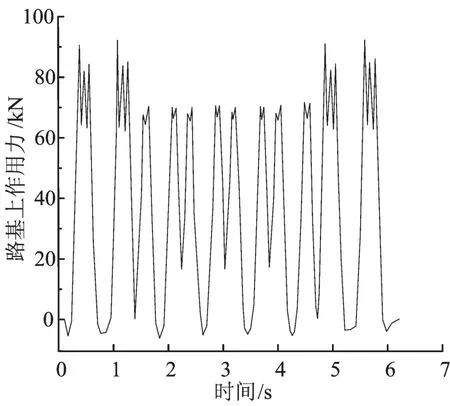
图2 路基上作用力时程曲线Fig.2 Time-history curve of force on the roadbed

为了对基坑在不同开挖工况条件下路基及和基坑边坡在列车动载下的瞬态稳定性进行比较，建立了5种不同工况下的有限元计算模型。

其中，工况1分析基坑土体尚未开挖时列车动载下铁路线路中心及基坑周围土体的动变形，与开挖后线路及基坑的变形情况进行对比分析；工况2分析第1级边坡放坡开挖完成、而锚杆支护尚未施作时线路中心及基坑周围土体的动变形情况；工况3分析第2级边坡放坡开挖完成、第1级边坡锚杆已完成、第2级边坡锚杆支护尚未施作时线路中心及基坑周围土体的动变形情况；工况4分析基坑开挖到第2层支撑位置、第1道支撑已完成，但第2道支撑尚未施作时线路中心及基坑周围土体的动变形情况；工况5分析基坑开挖至底层、第3道支撑及底板尚未施作时线路中心及基坑周围土体的动变形情况。

实际施工时并不是待每级边坡开挖完成后才施作锚杆，而是在放坡开挖的同时对边坡进行支护。因此本文选取施工过程中各最不利工况进行分析，以得到对稳定性分析有利的结论。

本文采用Newmark隐式直接积分法求解运动方程，采用Rayleigh阻尼作为体系的阻尼。资料表明[8]，岩土介质的阻尼比一般在ξ=0.02～0.24范围内。本文取ξ=0.02[9]，α=0.24887，β=0.00006。

用有限元法求解时域内的动力问题时必须保证计算过程的稳定性。如果时间步距Δt选取过小，则计算过程耗费机时，同时累积误差会影响到计算精度。如果时间步距Δt选取过大，则会损失高频成份，并使计算精度降低，甚至导致计算不收敛。本文取时间步长Δt＝0.01 s，总共计算600时步，计算总时长6 s。

3 计算结果及分析

图3与图4为邻近铁路的深基坑工程在不同开挖工况下，列车动载下路基中心点位置的水平和竖向动位移时程曲线。工况一下路基中心点位置的最大竖向动位移约为1.4 mm，这与铁科院、西南交大、中南大学、北京交大等单位对多条线路路基及过渡段的动力特性测试分析结果:基床动变形最大值约为1 mm[10]接近。因此可以认为本文数值模拟计算所选取的参数是合理的，继续对后续各工况进行数值模拟分析。从图3中可以看出，前3个工况下路基中心点位置的水平动位移比较接近，最大值约0.3 mm；工况4路基中心点位置的水平动位移突然增大，最大值约为0.67 mm；较前3个工况增大123.3%；工况5路基中心点位置的水平动位移与工况4基本相当。

从图4中可以看出，路基中心位置的竖向动位移也有类似规律:前3个工况下路基中心点位置的竖向动位移比较接近，最大值约1.4 mm；工况4与工况4路基中心点位置的竖向动位移基本相当，最大值约为2.0 mm，比前3个工况的最大动位移增大43.8%，但均不超过我国铁路路基动变形3.5 mm的控制标准[11]。

图5与图6为邻近铁路的深基坑工程在不同开挖工况下，列车动载下坡顶的水平和竖向动位移曲线。从图中可以看出，不同开挖工况列车动载下基坑边坡坡顶的竖向位移规律与路基中心点位置的变化规律是类似的。前3个工况下坡顶的水平、竖向动位移均比较接近，坡顶最大水平动位移为0.24 mm，工况4和工况5坡顶的水平动位移较为接近，最大动位移约为0.6 mm，较前3个工况下增大150%。前3个工况下坡顶的最大竖向动位移为0.72 mm，工况4和工况5坡顶的竖向动位移均比较接近，最大竖向动位移约为1.0 mm，较前3个工况下增大38.9%。

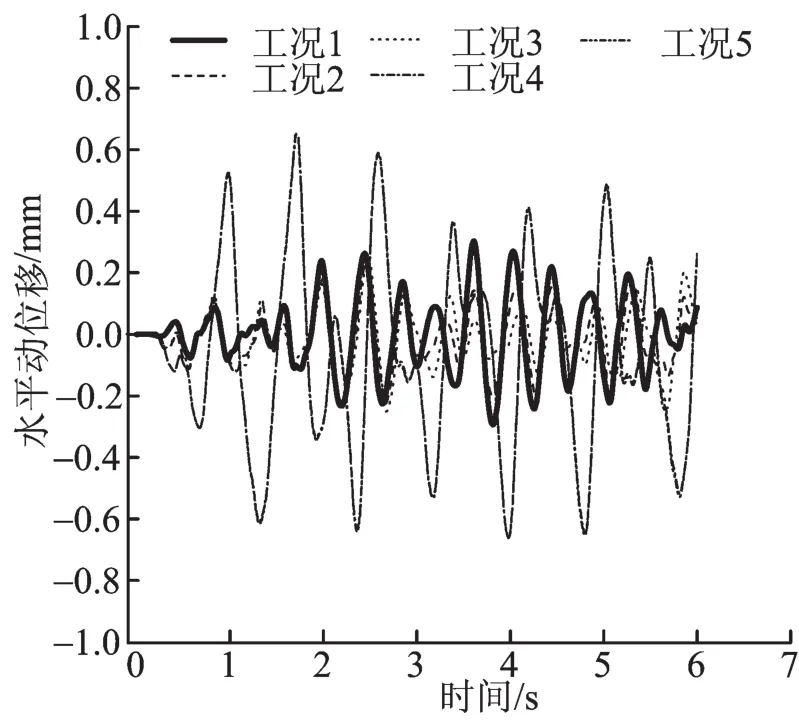
图3 路基中心点水平向动位移时程曲线Fig.3 The horizontal displacement of the subgrade centre

图4 路基中心点竖向动位移时程曲线Fig.4 The vertical displacement of the subgrade centre

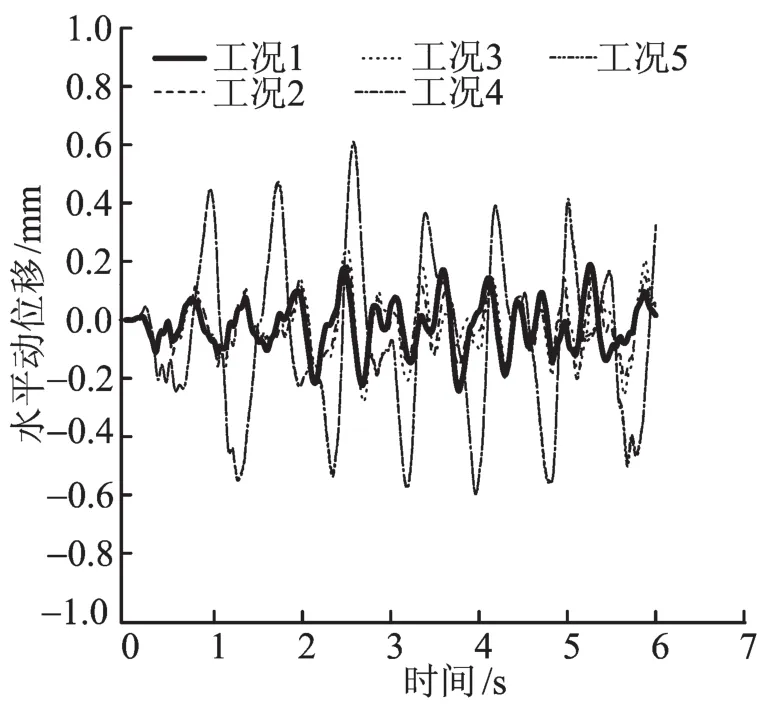
图5 坡顶水平向动位移时程曲线Fig.5 The horizontal displacementof the slope crest

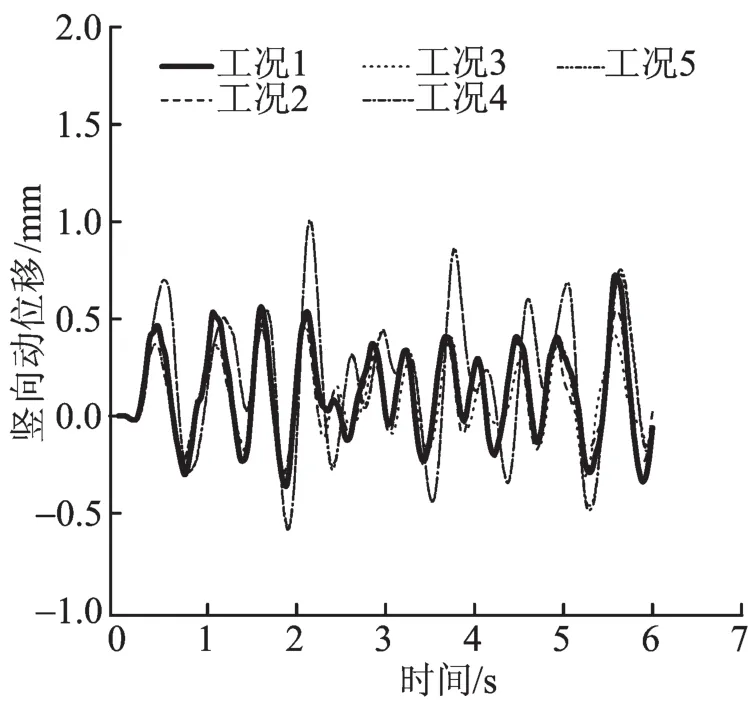
图6 坡顶竖向向动位移时程曲线Fig.6 The horizontal displacement of the slope crest

由以上数据可知:与周围介质未开挖、非扰动状态下路基竖向和水平动位移相比，两级放坡开挖过程中，邻近基坑的铁路路基中心及边坡坡顶处的竖向和水平动变形并无明显变化，说明水泥土搅拌桩和锚杆支护两项地基和边坡的加固措施对控制路基中心及基坑周围土体在列车动载下的变形有较好的作用。当基坑开挖至第2道支撑位置处，第1道支撑施作完成时（工况4），邻近基坑的铁路路基中心处及边坡坡顶处的动位移显著增大。当基坑开挖至第3层支撑位置处，第1道支撑施作完成时（工况5）时，邻近基坑的铁路路基中心及边坡坡顶处的竖向和水平动变形与上一工况相比无明显变化。

4 结论

前述分析表明，不同开挖工况下，列车荷载引起的路基－基坑体系的动位移存在差异:基坑开挖过程中，路基中心及基坑边坡坡顶的水平和竖向动位移均呈增大趋势；路基中心处的竖向动位移最大为2.0 mm，小于铁路路基动位移3.5 mm的控制标准，说明施工过程中采用的各项保护措施是有效的。同时，水平动位移增长率大于竖向动位移增长率，但从绝对值而言，仍以竖向动位移为主。此外，当坑内第1道支撑施作完成，开挖至第2道支撑以下时，路基中心及边坡坡顶处的动位移显著增大；当基坑内第2道支撑施作完成，开挖至第3道支撑位以下时，路基中心及边坡坡顶处的竖向和水平动变形与上一工况相比并无明显变化，说明开挖坑内第1层土时是基坑施工过程中较为危险的时刻。为此，施工过程中应加强监测，严格控制位移变化。

[1]王卫东，徐中华.预估深基坑开挖对周边建筑物影响的简化分析方法[J].岩土工程学报，2010，32（S1）:32-38.

[2]张晨明，董秀竹.新线施工对既有线车站影响分析[J].铁道工程学报，2006（9）:85-87.

[3]罗锟，雷晓燕.沪宁城际铁路基坑开挖对既有线动态影响分析[J].铁道工程学报，2010（9）:5-8.

[4]毕湘利，周顺华.列车振动荷载对邻近深基坑的既有站变形影响[J].同济大学学报:自然科学版，2004，32（12）:1599-1602.

[5]白冰，李春峰.地铁列车振动作用下近距离平行隧道的弹塑性动力响应[J].岩土力学，2009，30（1）:123-128.

[6]练松良.轨道工程[M].上海:同济大学出版社，2006:133-135.

[7]曹艳梅，夏禾.运行列车对高层建筑结构的振动影响[J].工程力学，2006，23（3）:162-167.

[8]林刚.列车振动对地铁重叠隧道结构力学行为的影响[J].铁道建筑技术，2006（3）:9-11.

[9]袁晓铭，孙锐等.常规土类动剪切模量比和阻尼比试验研究[J].地震工程与工程振动，2000，20（4）:136-139.

[10]肖军华.提速列车荷载下粉土的力学响应与路基稳定性研究[D].北京:北京交通大学，2008:15.

[11]王炳龙，杨龙才，等.高速铁路路基工程[M].北京:中国铁道出版社，2007:32-41.