客运专线车－线－桥垂向耦合系统振动的特性

陈 松，雷晓燕，房 建

（华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌330013）

随着我国国民经济的不断快速发展，交通成为制约发展的主要瓶颈，因此发展高速、重载铁路势在必行。而高架线路作为客运专线的主要形式（以京沪高铁为例，全线有73%的部分是桥梁结构），高速列车通过高架桥梁引起结构的振动问题成为当前的研究热点，各国专家在理论和应用方面都做了大量的工作。20世纪80年代起，国内外学者已经比较深入的研究了高速列车和重载列车的车辆－轨道系统动力学，提出了许多计算模型和计算方法。华东交通大学雷晓燕教授[1-3]提出了车辆－轨道－桥梁垂向耦合振动模型，利用有限元法建立了耦合振动方程，运用Newmark-β方法求解动力学方程。台湾成功大学朱圣浩教授等[4-5]采用有限元的方法，在建立车辆－桥梁－大地耦合振动的三维有限元模型时，将列车模拟为动轮单元，大地采用三维块体单元模拟，研究了高架轨道引起周边建筑物的环境振动。日本学者佐藤裕等[6]在考虑计算高频振动和模拟轨道不平顺引起的动力响应开发了比较完善的模型。Sato[7]使用他的集总参数模型“半车－轨道”研究了轨道动力响应及轮轨接触振动的产生和传播。以上文献分析中，车辆－轨道－桥梁耦合模型通常考虑有砟轨道，针对无砟轨道的情况并不多见，特别是将车辆、无砟轨道和桥梁作为一个大系统考虑。本文基于这些情况建立了高速列车－无砟轨道－桥梁耦合系统，并将这一大系统分为车辆－无砟轨道、无砟轨道－桥梁两个子系统，这两个子系统通过轮轨相互作用力耦合，得到大系统的动力学方程。用Newmark-β方法求解动力学方程，并利用Matlab语言编制了相应的程序代码。

1 车辆单元模型

基于雷晓燕教授的车辆－轨道－地基耦合系统模型[1-3]，本文对车辆单元做了以下假设:将每节车厢以单轮为单元分成4个独立动轮单元，每个动轮单元考虑一、二系弹簧（如图1），这样可以有效减小模型的自由度，简化计算。在单轮模型中，车体、转向架和车轮考虑只沉浮振动，每段钢轨单元上两个节点考虑竖向位移和转角，因此单轮模型有7个自由度。如图1所示，mc表示车体的质量；mt表示转向架的质量；ks1，ks2表示车辆一、二系悬挂刚度；cs1，cs2分别表示车辆一、二系悬挂阻尼；mw表示车轮的质量；kc表示轮轨间接触刚度；vc为车体沉浮振动的位移、；vt为转向架沉浮振动的位移；vw表示车轮的竖向位移；v1，v2表示钢轨两端的竖向位移；θ1，θ2表示钢轨两端的转角。如图1，设钢轨1点和2点距离为l，轮轨接触点3点离1点距离为x。可以将单轮单元的节点位移向量表示:

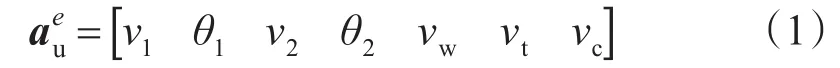
假定梁的位移模式:

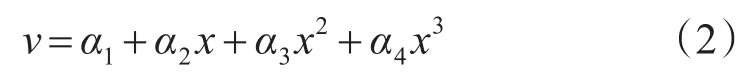
因此可以得出其插值函数:

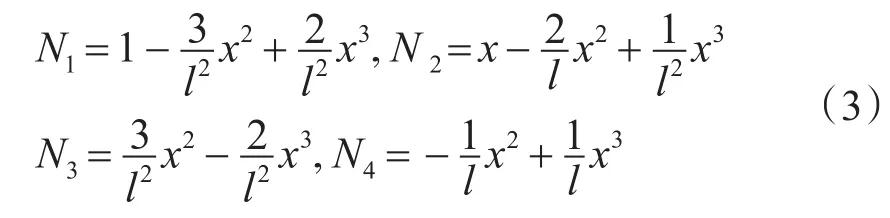
将单元中各个节点的位移使用单元位移向量和插值函数表示，运用Hamilton原理:

式中:L为Lagrange函数，L=Τ-V；Τ为动能；V为势能；R为耗散能。

因此可以单轮单元的动能、势能和耗散能，最后得出动轮单元的质量矩阵、刚度矩阵和阻尼矩阵。

为了更好模拟真实情形，本文考虑两节车厢，根据以上车辆单元假设，其动力学方程可通过单轮单元叠加得到。

2 无砟轨道－桥梁单元模型

我国最新客运专线基本上使用无砟轨道，大部分采用CRTSⅡ板式轨道，因此本文轨道模型采用CRTSⅡ板式无砟轨道，将轨道－桥梁结构简化为一层离散、三层连续的四层梁单元模型（图2），分别为钢轨、轨道板、混泥土垫层和桥梁。模型考虑各个节点的沉浮和点头振动，共有16个自由度。图2中:v1，v5表示钢轨的竖向位移，θ1，θ5分别表示钢轨的转角，csy1和ksy1分别表示轨下垫层的阻尼系数和支承弹性系数；v2，v6分别表示轨道板的竖向位移，θ2，θ6分别表示预制轨道板的转角，csy2和ksy2分别表示轨道板下CA砂浆层的阻尼系数和支承弹性系数；v3，v7表示混凝土垫层的竖向位移，θ3，θ7表示混凝土垫层的转角，csy3和ksy3分别表示混凝土垫层下桥梁的阻尼系数和支承弹性系数；ν4，ν8表示桥梁单元的竖向位移，θ4，θ8表示桥梁单元的转角。

图2 CRTSⅡ板式轨道简化模型Fig.2 CRTSⅡslab track and simplified model

从图2中我们可以定义无砟轨道－桥梁模型的节点位移向量:

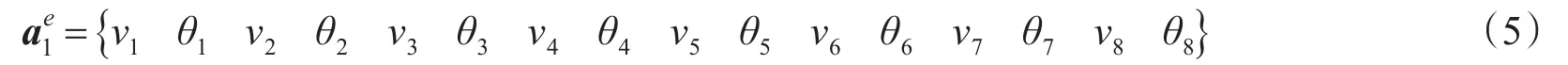
同样为了建立无砟轨道－桥梁单元的有限元方程，推导出插值函数，利用Hamilton原理，得出无砟轨道－桥梁单元的弹性势能、动能和耗散能再推导出无砟轨道－桥梁单元的刚度矩阵、质量矩阵和阻尼矩阵。

3 车辆－无砟轨道－桥梁耦合系统有限元方程

通过前两部分得两个子系统的动力学方程，两个子系统通过轮轨相互作用力耦合，相互作用力遵循赫兹公式，得出大系统动力学方程。相应得出大系统单元的刚度矩阵、质量矩阵和阻尼矩阵，分别为ku，mu，cu和kt，mt，ct。最后得出车辆－无砟轨道－桥梁竖向耦合系统的动力学有限元方程:

式中:

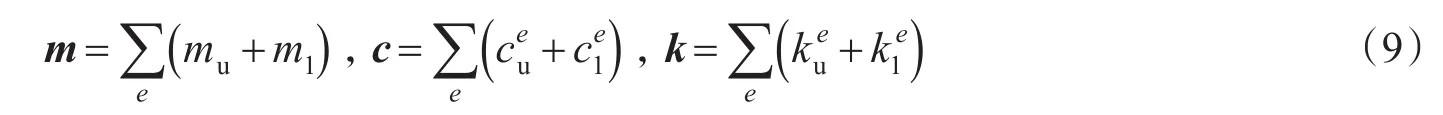
式中:Q为耦合系统的荷载向量；a为耦合系统的位移向量。运用Newmark-β方法解动力学方程，在Matlab软件中编制程序，实现解动力学方程。

4 车辆－无砟轨道－桥梁耦合系统竖向振动分析

将以上得到的动力学方程可利用Newmark-β方法求解，通过Matlab语言编写软件实现。模型参数根据我国最新客运专线的车辆和无砟轨道参数确定，列车时速取为300 km·h-1。

在轮轨动力学计算中，常用的不平顺谱有3种:美国的轨道谱、德国的轨道谱和我国干线铁路轨道谱，但它们都是有碴轨道不平顺谱。由于我国客运专线（特别是高速铁路）主要采用无碴轨道，因此在车辆轨道系统耦合振动中选择不平顺轨道谱是一个非常困难的问题，至今也没有比较统一的观点，只能从国内外现有的3种铁路轨道谱中做出选择。根据无砟轨道特性和我国无砟轨道的规范，在这里选择使用相对最合理的德国低干扰谱，利用Matlab程序，根据我国最新的动车CRH3-380的技术参数（表1）和CRTSⅡ板式轨道的技术参数（表2）得到车辆－轨道－桥梁的竖向振动响应。主要技术指标为轮轨力；钢轨和轨道结构的位移、速度和加速度。

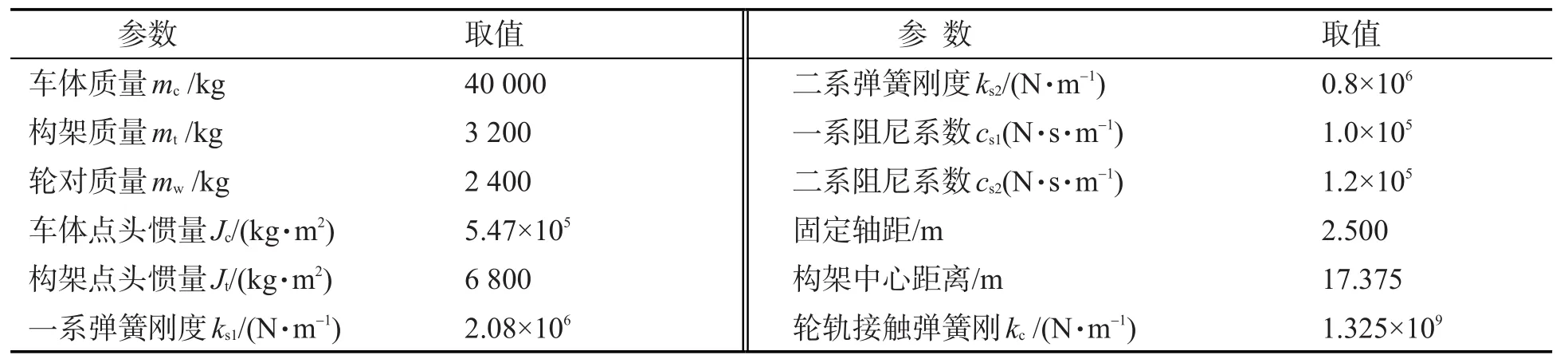
表1 和谐号高速动车CRH3车辆结构参数Tab.1 Structure parameters of“Harmony”CRH3 high-speed train

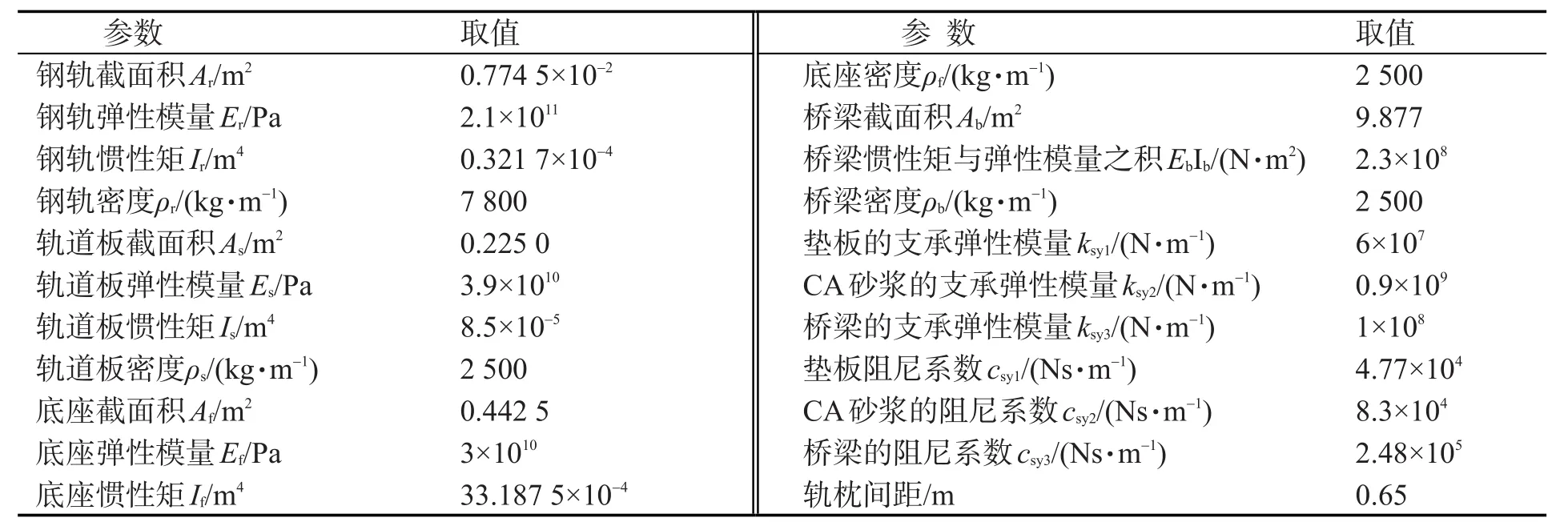
表2 CRTSⅡ型板式无砟轨道和桥梁结构参数Tab.2 CRTSⅡballastless track plate and bridge structure parameters

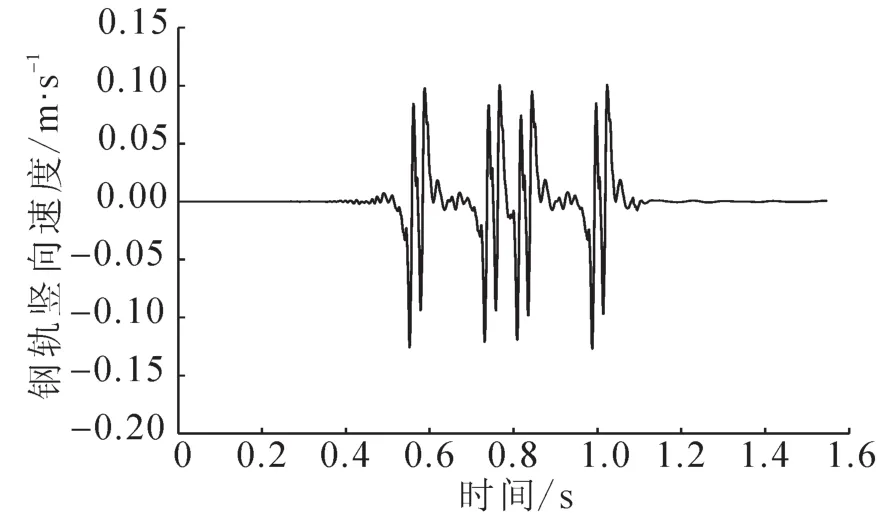
图3 轮轨接触力Fig.3 Interaction forces of wheel rail

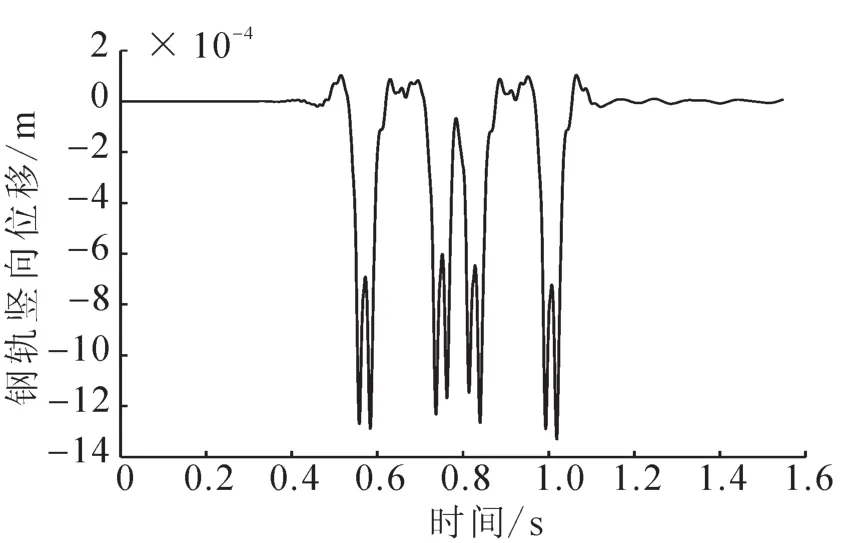
图4 钢轨竖向位移Fig.4 Vertical displacement of rail

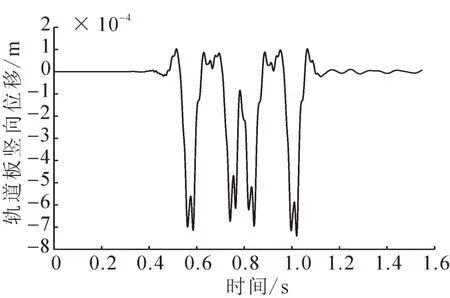
图5 轨道板竖向位移Fig.5 Vertical displacement of orbital plate

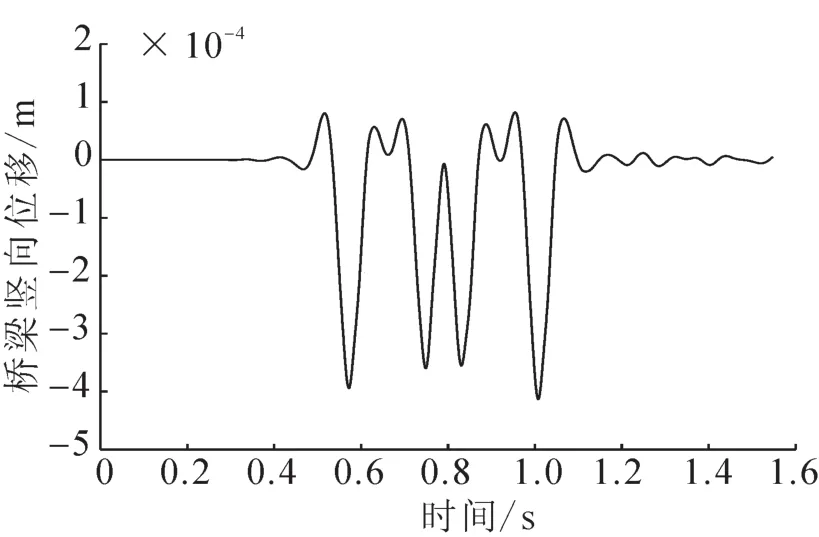
图6 桥梁竖向位移Fig.6 Vertical displacement of bridge

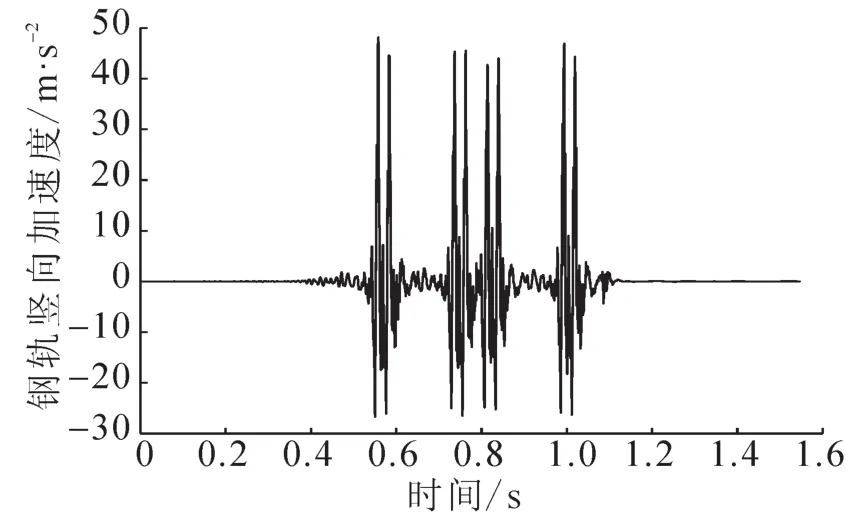
图7 钢轨竖向加速度Fig.7 Vertical acceleration of rail

图8 钢轨竖向速度Fig.8 Vertical speed of rail

对于图3，为轮轨接触力，图中当解稳定后可以看出力在72 kN附近以20 kN的幅值抖动，在列车时速为300 kN·h-1时这个波动范围并不是很大，这主要原因是由于不平顺样本采用了幅值不大于4 mm的德国低干扰谱。这也解释了我国高铁规范中线路高低不平顺幅值为4 mm。

对于图6～8，为位移响应图，对于钢轨的位移响应可以看出明显的8个轮，在与轨道板、桥梁的位移响应相比可以明显得出响应幅值在明显减小。图7～8，为钢轨的加速度与速度响应图，也可明显看出有8个轮，图4，图7和8为钢轨振动响应。

5 结论

通过对车辆模型的单轮简化，可以明显降低模型的复杂性，为在电子计算速度没有特别明显进步的情况下完成整车模型提供了可能性。对于轨道部分，考虑了4层梁单元，这为研究扣件、轨下垫层、CA砂浆层对减振降噪的影响提供了依据。本文在考虑高铁的特性下使用了最能反应无砟轨道高低不平顺的德国低干扰谱，从轮轨力中可以与规范相互验证正确性，得出了列车时速在300 kN·h-1情况下的动力特性，为我国高铁设计和运行提供一些理论依据。

[1]雷晓燕.现代铁路理论研究[M].北京:中国铁道出版社，2006:51-66.

[2]雷晓燕.高速列车诱发地面波与轨道强振动研究[J].铁道学报，2006，28（3）:78-82.

[3]雷晓燕，张斌，刘庆杰.列车－轨道系统竖向动力分析的车辆轨道单元模型[J].振动与冲击，2009，29（3）:168-173.

[4]JU SHENHAW，LIN HUNGTA.Analysis of train-induced vibrations and vibration reduction schemes above and below critical Rayleigh speeds by finite element method[J].Soil Dynamics and Earthquake Engineering，2004，24（4）:993-1002.

[5] JU SHENHAW，LIN HUNGTA.A simple finite element model for vibration analyses induced by moving vehicles，International Journal for Numerical Method in Engineering[J].Soil Dynamics and Earthquake Engineering，2006，68（12）:1232-1256.

[6]佐藤裕.轨道力学[M].卢肇英，译.北京:中国铁道出版社，1981:33-45.

[7]佐藤吉彦.新轨道力学[M].徐涌，等，译.北京:中国铁道出版社，2001:54-61.