灰色预测在高铁路基沉降预测中的应用

2011-07-05秦晓光杨龙才

华东交通大学学报 2011年5期

秦晓光，杨龙才

（同济大学道路与交通工程教育部重点实验室，上海201804）

高速铁路对轨道平顺性的要求很高，而轨道的平顺性直接受到地基工后沉降的影响，因此高速铁路对工后沉降要求非常严格，高速铁路设计规范规定路基“工后沉降不宜超过15 mm”[1]。因此对工后沉降的准确把握已成为高速铁路沉降变形控制的关键技术之一。目前的高铁建设都需进行沉降观测，规范中对测点布设原则及观测频次均有细致的规定[1]，既体现了高铁建设过程控制的理念，又为工后沉降预测模型的建立提供数据。

目前工后沉降预测的方法主要有理论计算法和根据实测资料推算沉降量与时间关系的预测方法。理论计算法包括传统方法和数值方法。传统方法即分层总和法。数值方法则是根据固结理论，结合土的本构模型，计算地基各种沉降量的差分法、有限元法和边界元法。其中传统方法计算结果往往与实际偏差较大，而数值分析法不仅建模工程量大，所需土的本构模型中的参数也需通过大量实验获得，且较难确定，所以难以在工程中得到普遍使用。根据实测资料推算沉降量与时间关系的预测方法包括确定性预测方法和不确定性预测方法。确定性预测方法如指数曲线法、对数曲线法、双曲线法、星野法、Asaoka法。不确定预测方法是随着系统理论与计算科学的发展而发展起来的方法，已得到了广泛应用，如灰色理论预测法以及神经网络方法等。灰色模型法具有可采用较少的数据对工后沉降进行预测等优势，通过对数据的处理建立微分方程发掘数据内部的变化规律[2]，进而对工后沉降进行预测。

国内很多学者采用累计沉降作为原始数据建立灰色预测模型，通过等维新陈代谢模型[3]或者针对沉降发展趋势，初期发展较快，后期逐渐收敛特点，采用缓冲算子对初期数据进行弱化，进而减少长期预测数据无限增长的结果[4]。其中等维新陈代谢模型只能进行短期或者中期的沉降预测，对后期沉降预测结果难以保证。采用弱化缓冲算子进行初期数据处理时，缓冲算子节数需根据沉降发展趋势实验确定。罗战友等[5]对比理论沉降发展曲线形态，认为全过程沉降量与时间关系成S形曲线，并采用灰色verhulst模型对建筑物沉降实测值进行预测，其预测结果较为满意。但是，在高速铁路路基填筑期间，受到碾压机或其他机械荷载的作用，沉降数据曲线难以呈现完整的S形，这时verhulst模型的使用就受到了局限。

针对高速铁路路基沉降的特点，以某高铁路基施工现场施工期及堆载预压期的沉降观测数据为基础，通过对实测数据初步分析发现，因路基高度、填筑速率、地基处理形式及地质情况的不同，地基沉降收敛趋势形态有所差别。并选取典型沉降形态曲线进行工后沉降预测，与双曲线法及三点法（固结对数配合法）进行对比，评价灰色系统预测模型在高铁路基工后沉降预测中的适用性。

1 高速铁路路基沉降曲线形态分析

1#、2#曲线为路基沉降板沉降时间曲线图，3#曲线为涵洞沉降时间曲线图，见图1，2。从图中实测数据看出，1#曲线路基填筑期施工期较长，荷载增加缓慢，在路基填筑期及堆载预压期沉降速率均比较缓慢。2#曲线路基填筑施工期较短，沉降速率相对较快，堆载预压期前期较快，后逐渐趋于稳定。3#曲线涵洞施工期荷载较小，沉降发展速率较慢，在涵洞顶路基填筑期间沉降发展速率最快，在堆载预压期沉降速率基本趋于稳定。

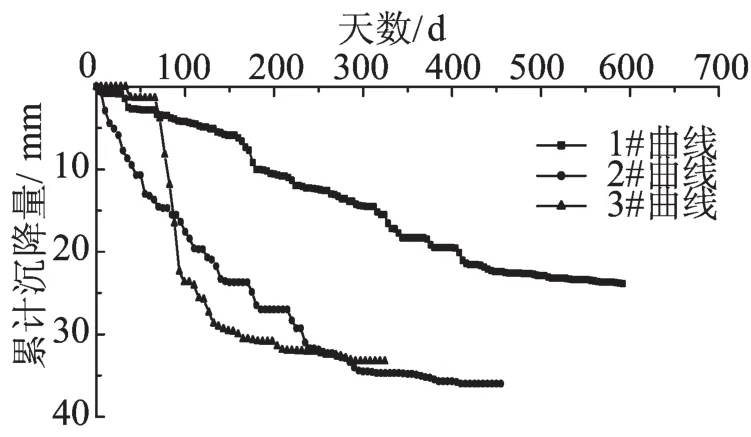
图1 沉降曲线图Fig.1 Curves of settlement

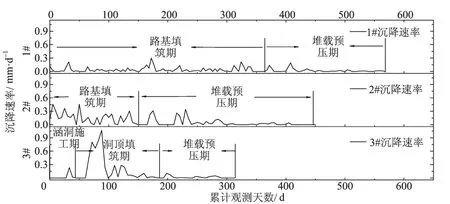
图2 沉降速率对比图Fig.2 Comparison chart of settlement rate

因此在对大量沉降观测数据汇总的基础上将沉降发展趋势分为3个类型，见图3，第1种收敛趋势较慢，第2种收敛趋势适中，第3种收敛趋势较快。本文将采用灰色理论分别对上述3种类型的沉降时间曲线形式进行预测。并与传统预测方法进行比较。

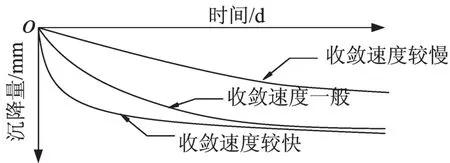
图3 沉降形态分类示意图Fig.3 Classification chart of settlement morphology

2 灰色系统预测方法及检验

2.1 灰色系统理论预测方法

完全未知的对象被成为“黑箱”这早已被人们所接受，在灰色理论中用“黑”表示完全未知的信息，“白”表示完全已知的信息，由于环境对系统的制约而得到的离散型的数据被定义为“灰”[6]。灰色预测模型是利用贫信息，小样本进行系统后期发展预测的模型。通过对原始数据进行变换不断白化，然后建立微分方程，其解作为动态系统的控制模型[7]，进而预测沉降的发展趋势。

灰色微分方程x(0)()t+az(1)(t)=b的最小二乘估计参数列满足:

对定理1中的灰色微分方程求解，得到其通解为

式中:C为积分常数，需要通过一个定解条件来确定。在目前采用的预测模型中一般假定:

将式（4）带入式（3）得

从而式（3）在式（4）条件下的特解为

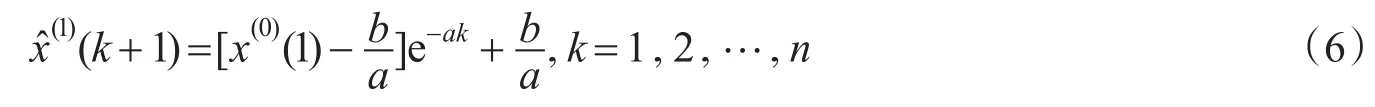
即为灰色预测模型GM（1，1）的时间响应序列。

对于GM（1，1）模型只有通过精度检验才能用于预测，本文采用后验差及小误差概率检验。后验差检验模型精度等级[8]参照表见表1。

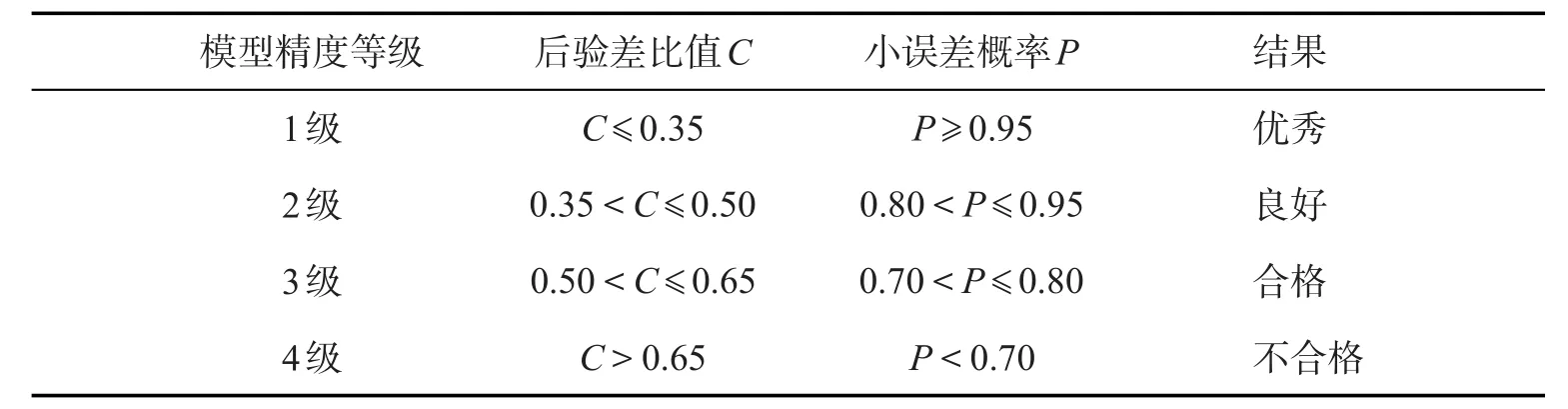
表1 后验差检验模型精度等级参照表Tab.1 Reference table of precision grades of post-test

2.2 预测结果及精度检验

由于灰色理论进行预测的前提之一是要求数据等时距分布，本文采用样条插值的方式进行等时距变换[9]。在地基沉降预测中将单次沉降作为原始数据x（0），经过一阶累加算子1-AGO作用后即为累计沉降，从而可以导出x（1）的控制方程来预测沉降的发展趋势。文中灰色预测模型采用堆载预压期的数据进行预测。

使用MATLAB编写灰色预测及后验差检验程序，分别用GM（1，1）模型对1#，2#，3#沉降曲线进行预测，并进行检验，结果见表2。可以看出灰色预测模型等级较高，故认为该模型能够对随机性较大的沉降实测数据进行良好预测。结果见表3。

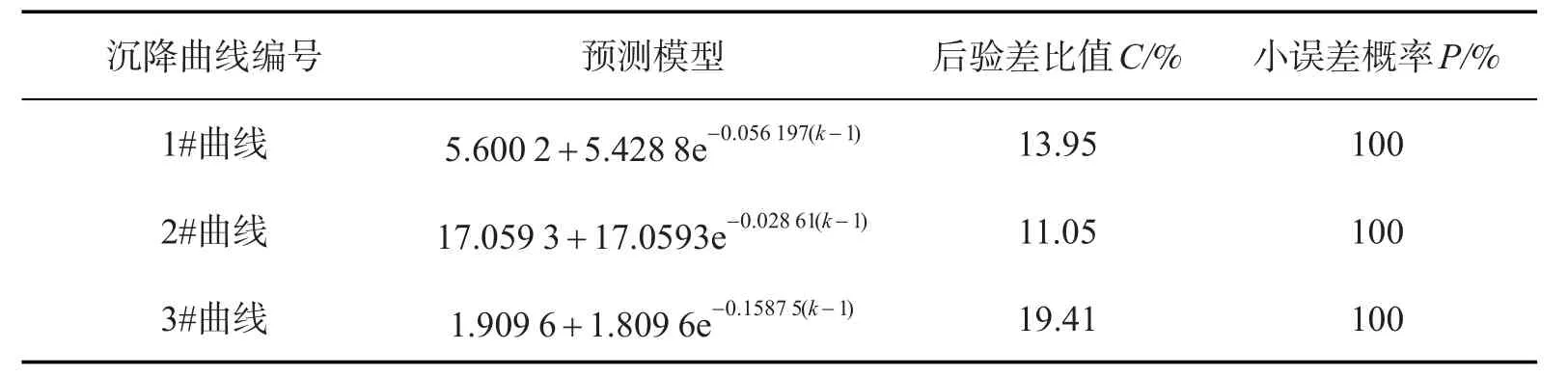
表2 预测模型及精度检验Tab.2 Prediction model and precision inspection

3 3种预测法对比及适用性评价

选取预测数据以荷载稳定后即与预压土堆载到设计标高的时间为起点，时间起止点见表3，分别采用灰色理论、双曲线法、指数曲线法对1#，2#，3#进行沉降预测。并与预压期最后一期数据为对比值。对比3种预测结果，发现除3#曲线外，其他两条曲线灰色理论值与实测结果最相近，其中3#曲线预测值均较最后一期观测值小，原因可能是预测数据选取时间终点以后地基又发生了少量的沉降突变，因而造成预测值均较实测值偏小。

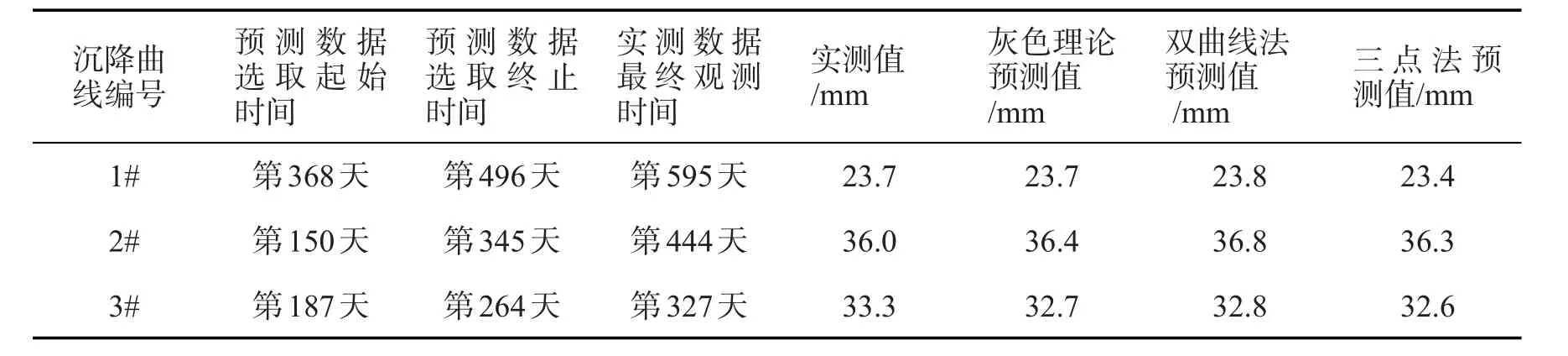
表3 数据选取起止点及预测结果Tab.3 Starting and ending time of the selected data and predicting results

对3条曲线的最终沉降进行对比，其预测结果见表4。其中灰色预测模型中后期沉降量随时间发展极为缓慢，因此这里取预测数据最终观测时间后第500天的数据作为最终沉降。对比预测结果数据可以看出双曲线法预测的最终沉降最大，三点法预测的最终沉降最小，灰色理论预测的最终沉降适中；相对误差均值及残差平均值相差不大。

表4 3种预测方法结果对比Tab.4 Result contrast of three prediction methods

对比3种预测方法的结果可以看出，双曲线法预测的沉降曲线收敛较慢，预测最终沉降结果最大，指数法预测的沉降曲线收敛结果最快，预测最终沉降结果最小。由于高铁对工后沉降要求很小，地基处理的标准较高，因而一般沉降收敛速率较快，双曲线法在工后沉降的预测中结果往往偏大。三点法收敛速率较快，预测结果偏小，且选点不同往往预测结果也不同，受人为因素的干扰。灰色理论预测模型预测结果比较合理，得到的预测结果较为理想。