一种改进的电离层参数联合反演方法

杨东升，焦培南，2，柳 文，，2王俊江

(1.中国电波传播研究所青岛分所，山东 青岛 266071;2.电波环境特性及模化技术国家重点验室，山东 青岛 266071)

0 引言

目前国内外不少学者基于单独的返回散射探测结果或斜向探测结果反演电离层参数做了大量工作，取得了较好的成果［1～3］。但是，这些基于单一探测手段的反演算法有个共同的特点就是对初值选取要求比较苛刻，对测量误差也非常敏感，从而导致反演算法本身往往是不稳定的。实际工程应用中由于测量设备的精度及不可避免的噪声影响，最终得到的电离图往往存在不同程度的误差。电离层参数反演通过简化可转化为线性反演问题，因此利用正则化方法进行反演［4～6］有效改善了算法的稳定性。

反演问题的不稳定性，简单说是由于不能够提供足够的信息来确定一个唯一、稳定的解。文献［7］就是通过提供更为丰富的探测信息来提高反演的稳定性，提出了一种返回散射和斜向探测联合探测电离层，以及基于探测结果联合反演电离层参数的新技术。该新技术通过在返回散射探测覆盖区域内设置若干个斜测接收设备，从而实现一个返回散射探测系统和多个斜向探测系统对于同一区域的同时探测，并通过融合这两种探测信息实现对同一区域电离层参数的精确反演。文献［7］已通过仿真手段论证了该方法的可行性、稳定性和收敛性。但其并未充分考虑不同采样方式对反演结果的影响，另外其全局遍历寻优在一定程度上影响了反演的效率。本文通过引入粒子群优化算法，同时分析和优化反演时的数据采样方式，不仅实现了快速搜索，也有效提高了反演的稳定性和准确性。

1 采样方式对反演结果的影响

基于 QP 模型［8～9］的电离层参数反演中，需要对大量测量数据进行采样作为反演的输入，然而不同的采样数据也会影响反演的效果。下面假设QP模型参数为:fc=6.0 MHz，rb=200 km 和 rm=300 km，用仿真结果给出了仅包含舍入误差时，不同采样数据对于返回散射电离图反演和斜测电离图反演的影响。事实上，如果误差更大，这种影响作用会被进一步放大。

1.1 返回散射电离图反演

基于上述参数合成的返回散射前沿，如图1所示。

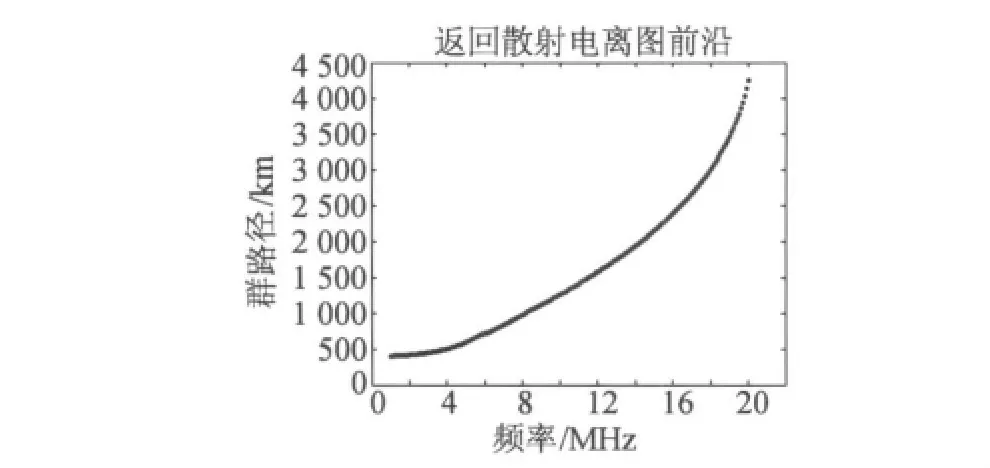
图1 合成的返回散射电离图前沿

基于粒子群优化算法对不同的采样数据分别进行多次反演，其中前六组数据频率间隔为1 MHz，最后一组为4 MHz，得到统计结果，见表1。

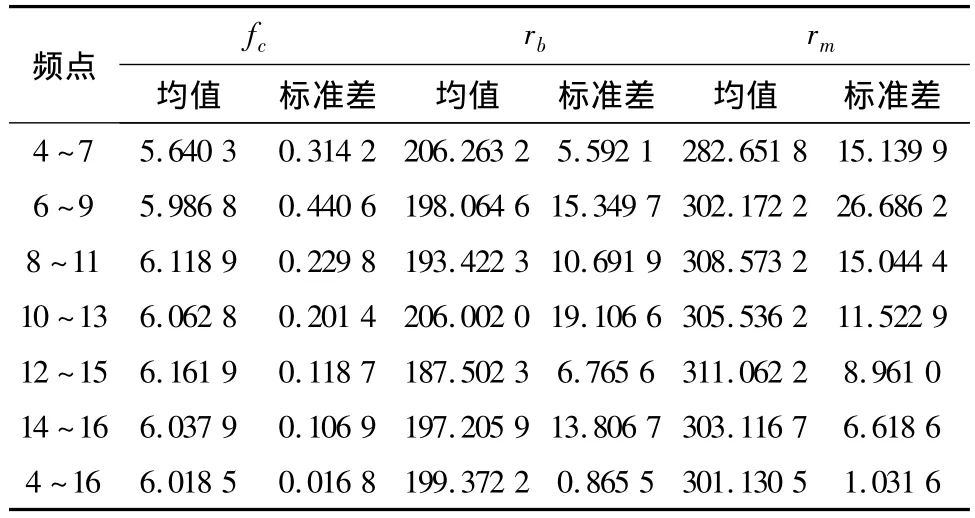
表1 返回散射不同频点对应的反演结果

上述的反演结果表明，局部的电离图由于其数据之间的很高的相关性，导致反演结果的不稳定，即便只是引入很小的舍入误差，每次反演的结果也会产生很大的不同。而使用频率相对分散并且群路径差异较大的数据，由于其对应的电离层信息更加丰富不仅可以有效克服这种不稳定性，同时能够减小测量误差对于反演结果的影响。

1.2 斜测电离图反演

基于上述合成的电离层参数合成的1000 km斜测电离图，如图2如所示。

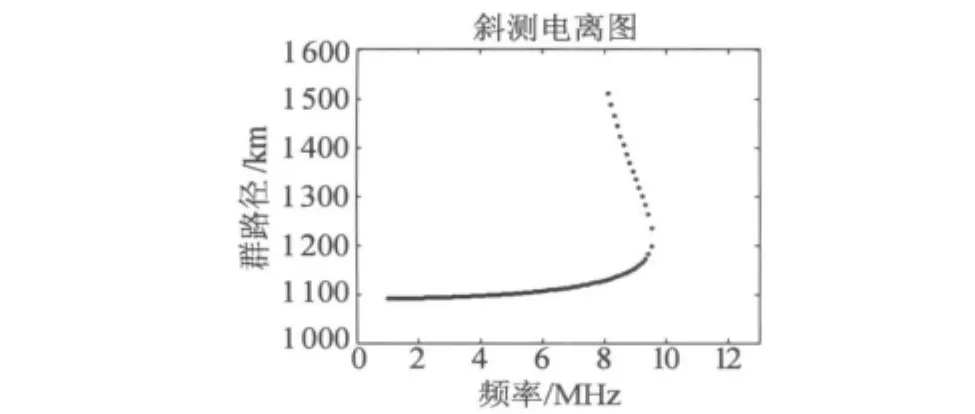
图2 合成的收发两地相距1000 km斜测电离图

分别基于以下四种采样数据进行反演:(1)选取低频段2～6 MHz的数据;(2)MUF附近9～10 MHz低仰角射线;(3)高频段8～10 MHz高仰角射线;(4)综合前三种情况。反演的统计结果见表2。

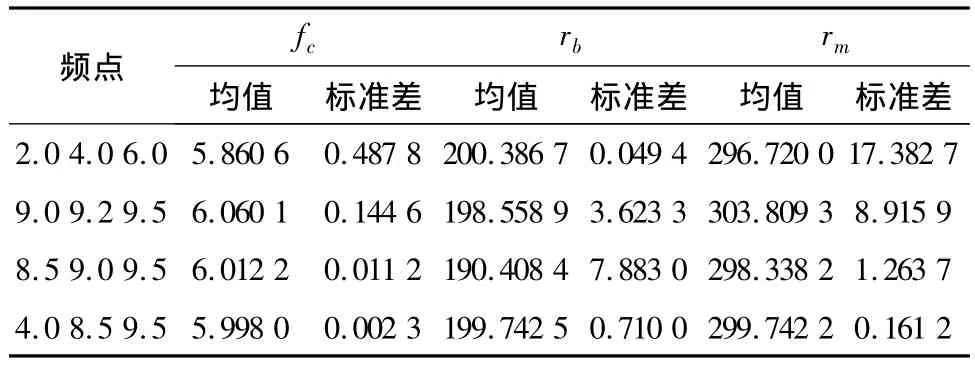
表2 斜测不同频点对应的反演结果

上述的反演结果表明，使用低频段数据反演可以得到稳定和准确的rb，而使用高角射线对应的数据进行反演可以得到稳定和准确的rm。根据上述四种采样数据的反演结果，可以得出结论:在利用斜测电离图进行反演时，应尽量选取数据包含低仰角射线、高仰角射线及MUF附近对应的射线。对于不完整的电离图也应使选择频率分布相对广和群路径差异明显的数据进行反演，能够提高反演的稳定性，同时减小了误差对于反演结果的影响。

多种探测数据联合反演是利用不同的探测手段获得更加全面电离层信息，而不同采样方式则是寻找一组更能代表当前探测电离图的数据，两者都是通过提供更为丰富的输入信息提高反演稳定性和精度。

2 粒子群优化算法

2.1 非线性反演问题

非线性反演问题通常分为两类［10］:拟线性反演方法和完全非线性反演方法。前者必须对原反演问题进行离散近似，通过不断迭代进行优化最终完成求解，其原理明晰、方法直接。后者是对原反演问题不进行局部近似直接寻优的方法。目前遗传算法［11］和模拟退火算法［12］已有应用于电离层参数反演，并取得一定效果。粒子群算法作为一种新型的全局寻优算法，短短数年已有很大发展，为更深入研究反演问题提供了一种新的方法。

2.2 粒子群优化算法原理

粒子群优化(PSO)［13～14］算法是通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种基于群体智能的全局随机搜索算法。其基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。

粒子群优化(PSO)算法将每个个体视为D维搜索空间中的一个粒子，其在进化过程中维护两个向量，即速度向量=［，…，］和位置向量=［，…，］，其中i表示粒子的编号，D是待求解问题的维数。粒子的速度决定了其运动的方向和速率，而位置则体现了粒子所代表的解在解空间的位置，是评估解质量的基础。同时每个粒子各自维护一个自身的最优位置向量(用pi表示)，整个群体维护一个全局最优，用g表示。通过对粒子设定评价函数，并根据每个粒子的各自最优位置和群体最优位置不断更新自己的飞行速度和所在位置，参见式(1)和式(2)，最终到达或逼近目标位置。

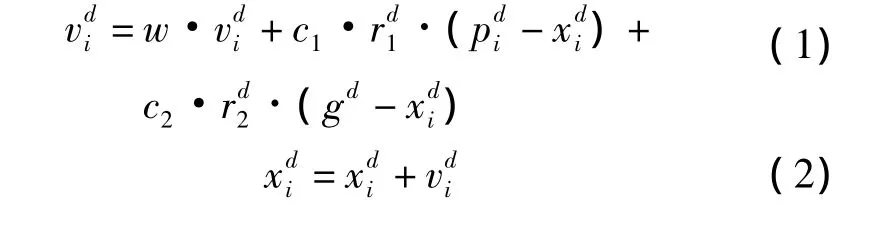
式中，w为惯性权重;c1和c2为加速常数;r1和r2为两个在［01］范围内的随机数。式(1)和式(2)中，i=1，2，…，M，M是该群体中的粒子的总数，此外粒子的速度被最大速度Vmax所限制，最大迭代次数为Gmax。

2.3 粒子群优化算法流

粒子群优化算法流程，如图3所示。

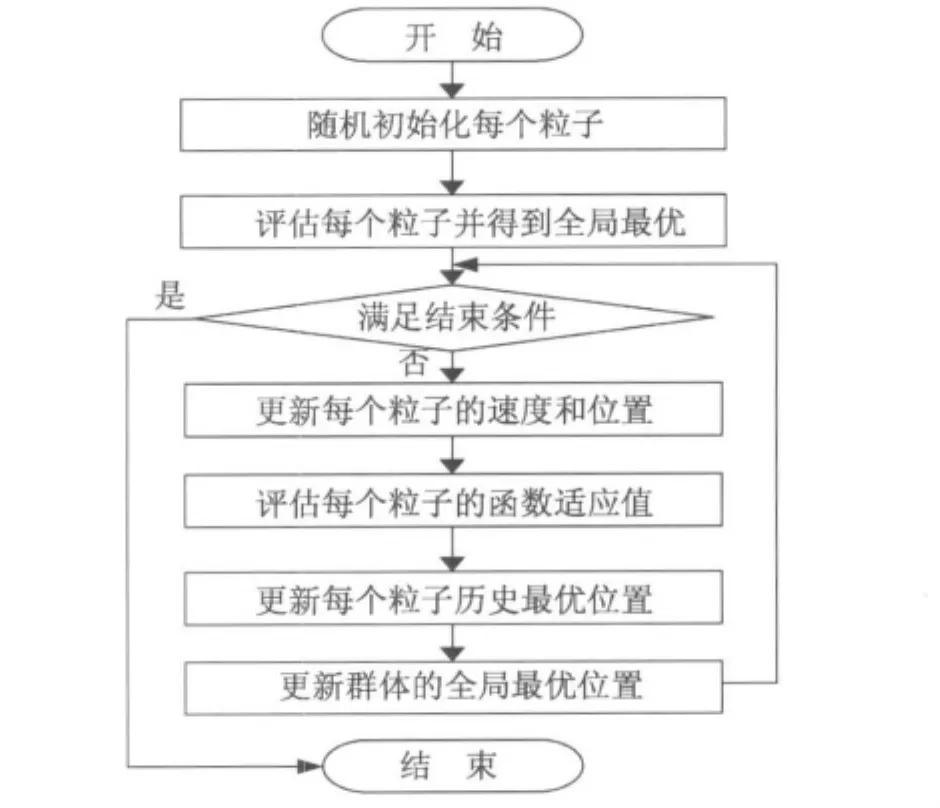
图3 粒子群优化算法流程

3 联合反演

3.1 联合反演的准则

QP模型参数的反演最终是要确定三个参数fc、rb和 ym。基于均方误差最小准则［7，15］，分别在返回散射电离图前沿和斜测电离图上取K1、K2个频率点，对应的返回散射电离图前沿上群路径观测值为P1i'，计算得到的群路径为P1i，对应的斜测电离图上的群路径观测值为P2i'，计算的群路径为P2i，计算值与观测值的均方误差为

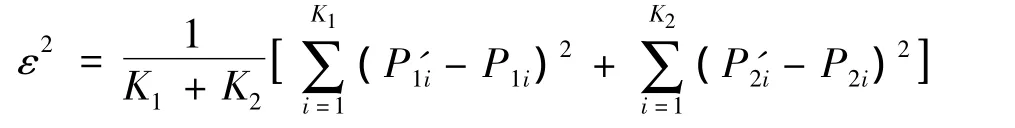
假设解空间为 Φ，则(fc，rb，ym)∈Φ。首先通过预测或者经验确定搜索域Φ。然后在搜索域内进行全局搜索并计算均方误差，均方误差最小时对应的电离层参数即为最优解。

3.2 联合反演实例

QP 模型参数:fc=6.0 MHz，rb=200 km 和 rm=300 km，斜向探测收发两地距离为1000 km。返回散射取K1=4，频率［481216］MHz对应的最小群路径，斜测取 K2=3，频率［4.08.59.5］MHz，其中8.5 MHz为对应的高角射线群路径，其他为低角射线对应的群路径。

粒子群算法参数:问题的维数D=3，群体规模设置为M=20，最大迭代次数 Gmax=200，w=1.0，c1=c2=2.0，搜索区间为 fc∈［4 8］，rb∈［140260］，rm∈［240 360］，为了便于搜索，将三个参数的搜索区间采用线性关系映射到［－11］上，统一设置每个参数的最小最大速度为－0.2和0.2。反演时，利用上节中提到的均方误差作为每个粒子的评价函数，评价函数值越小粒子越优良。

首先利用“测量真值”，即基于上述模型参数利用射线追踪得到的数据进行反演，结果见表3。

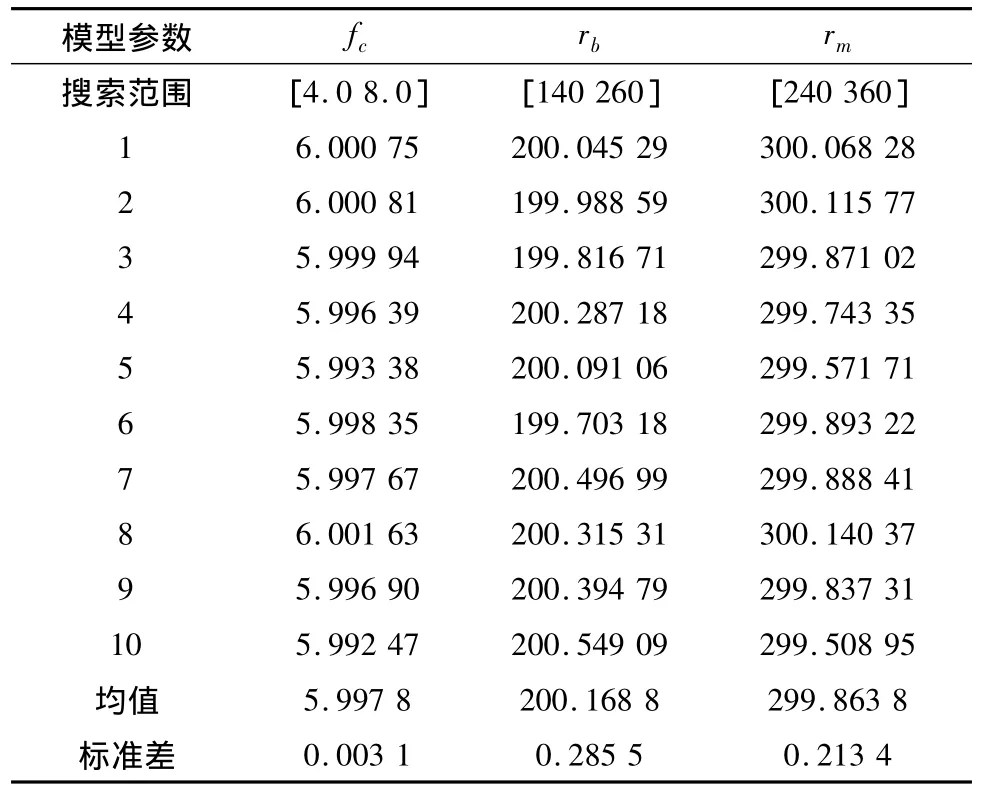
表3 利用“测量真值”进行10次反演的结果

上述反演结果表明，利用“测量真值”进行反演，该方法是稳定的很好的逼近真实值。

为了验证该方法在一定误差下仍然有很好的反演效果，对“测量真值”添加方差σd=20的随机误差，进行反演，结果见表4。

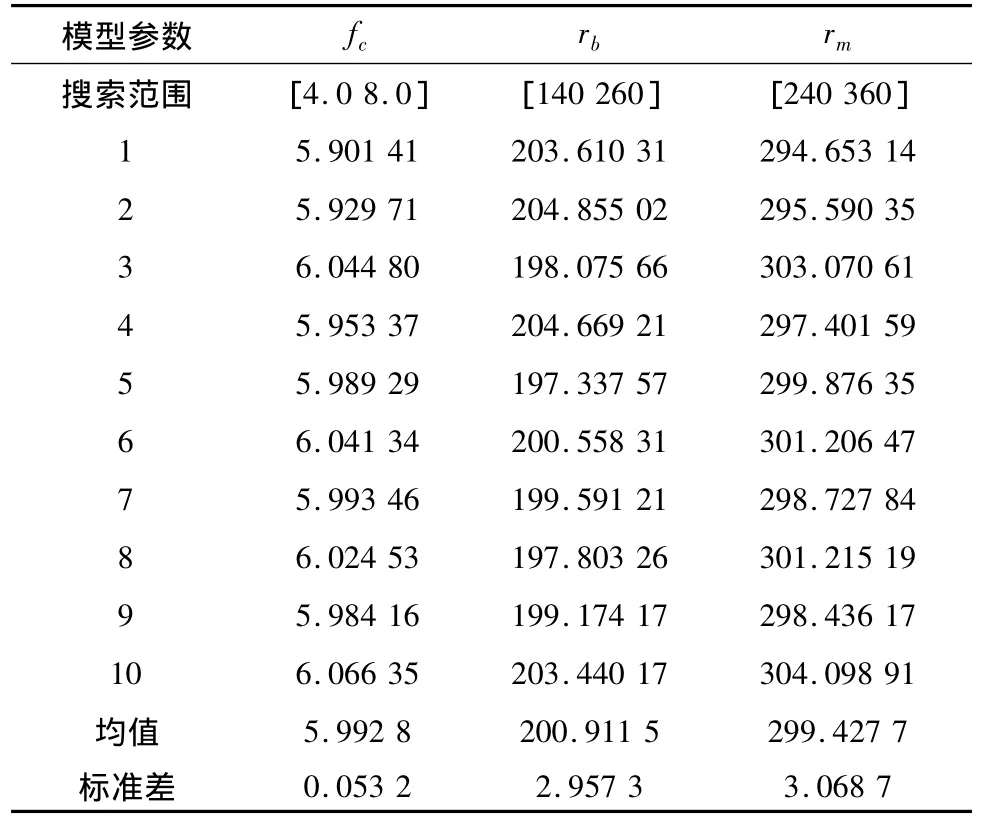
表4 利用含σd=20随机误差的数据进行10次反演的结果

上述反演结果表明，即便是在引入一定随机误差的情况下，该方法仍然是稳定收敛的，虽然每次反演结果都会有一定的偏差，但仍然在可以接受的范围之内。

4 结语

本文在文献［7］提出的利用返回散射和斜测电离图联合反演电离层参数方法的基础上，分析了不同采样方式对于反演结果的影响，优化了频点的选择，另外在反演中引入粒子群优化算法，该算法是一种群智能全局搜索算法，具有搜索速度快、搜索范围大、概念简单易于实现等特点。通过这些改进，联合反演的稳定性和准确性得到了很大的提高，并且迭代搜索次数明显减少，大大缩短了反演的时间，有一定的实用性。

［1］NARAYANA RAO N.Analysis of Discrete Oblique Ionogram Traces in Sweep-frequency Sky-wave High Resolution Backscatter［J］.Radio Sci.1975，10(2):149-153.

［2］NARAYANA RAO N.Inversion of Sweep-frequency Skywave Backscatter lLeading Edge for Quasiparabolic Ionospheric Layer Parameters［J］.Radio Sci.，1974，9(10):845-848.

［3］CHUANG S L.，YEH K C.A Method for Inverting Oblique Sounding Data in the Ionosphere［J］.Radio Sci.，1977，12(1):135-140.

［4］柳文，焦培南，王俊江.斜测电离图反演及其不稳定性研究［J］.电波科学学报，2003，18(6):597-601.

［5］FRIDMAN O V，FRIDMAN S V.A Method of Determining Horizontal Structure of the Ionosphere From Backscatter Ionograms［J］.J.Atmos.Terr.Phys.，1994，56(1):115-131.

［6］FRIDMAN S V.Reconstruction of a Three-dimensional Ionosphere from Backscatter and Vertical Ionograms Measured by Over-the-horizon Radar［J］.Radio Sci.，1998，33(4):1159-1171.

［7］杨东升，焦培南，程延锋，等.基于返回散射和斜测电离图联合反演电离层参数［J］.中国电子科学研究院学报，2010，5(5):503-507.

［8］DE VOOGT A H.The Calculation of the Path of a Radio-ray in a Given Ionosphere［J］.Proc.，1953，41(09):1183-1186.

［9］THOMAS A CROFT，HARRY HOOGASIAN.Exact Ray Calculations in a Quasi-parabolic Ionosphere with no Mag-netic Field［J］.Radio Sci.，1968，3(1):69-74.

［10］王彦飞.反演问题的计算方法及其应用［M］.北京:高等教育出版社，2007.

［11］谢树果.斜向返回散射探测电离层参数反演方法研究［D］.武汉:武汉大学，2001.

［12］BENITO E，et al.Inversion of Backscatter Ionograms Optimization by Using Simulated Annealing and Genetic Algorithms［C］//Geoscience and Remote Sensing Symposium 2008，Boston，MA.2008.

［13］KENEDY J，EBERHART R.Particle Swarm Optimization［C］//Proceedings of the IEEE International Conference on Neural Networks，Perth，Australia，IEEE Service Center，Piscataway，NJ，1995，4:1942-1948.

［14］梁艳春，吴春国，等.群智能优化算法理论与应用［M］.北京:科学出版社，2009.

［15］JULIEN CARATORI，GOUTELARD C.Derivation of Horizontal Ionospheric Gradients from Variable Azimuth and Elevation Backscatter Ionograms［J］.Radio Sci.，1997，32(1):181-190.