Frank码截获信号循环谱特征参数提取方法

张 鑫，刘 锋，刘 勇

(1.海军航空工程学院研究生三队，山东 烟台 264000;2.海军航空工程学院电子信息工程系，山东 烟台 264000)

0 引言

多相码调制技术广泛运用于低截获概率宽带信号［1］，Frank码信号是其中的一种典型应用。截获接收机对这些信号的侦测具有相当大的困难。传统的信号处理方法如能量检测法、功率谱密度分析无法提供Frank码信号参数的细微特征。近期的大量研究［2］表明:截获接收机可以通过采用循环谱特征分析方法改善处理增益，从而提高参数提取效果。

Frank码信号具有一阶和二阶循环平稳特性［3］，循环谱特征分析特别适用对这类信号进行参数提取。本文采用时域和频域两种循环普密度函数估计方法，得到Frank码信号的循环谱特征及其与信号参数对应关系，实现了在无先验知识条件下对Frank码截获信号关键参数(包括信号带宽B，载频fc，子码长度Nc，码率Rc，子码周期tm和调制周期T等)的有效提取。

本文研究了低信噪比(－6 dB)条件下Frank码截获信号［4］参数提取效果。Frank码设定为具有M个频率阶跃，每个频率上有M个采样相位。Frank码信号形式表示为

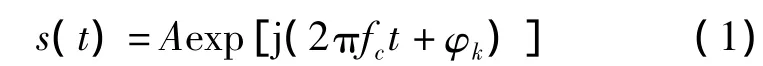
式中，φk为随时间改变的相位调制函数;fc为信号载频;A为幅度。Frank码的相位序列为

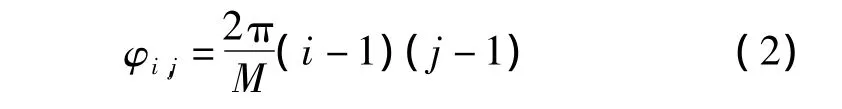
式中，i=1，2，…M，j=1，2，…M，M 也称作子码数。码长度Nc=M2，编码周期为T，码片时宽为tm，信号带宽为 B，则有 B=1/tm，T=Nc·。

1 循环谱特征分析

1.1 时间平滑FFT累积算法(TFAM)

循环平稳处理将信号变换至频率－循环频双频率域。循环谱特征分析关键是计算信号的循环相关函数和循环谱密度函数［6］。时间平滑FFT累积算法可以减少对循环谱估计的计算量［7］。其估计算子形式为

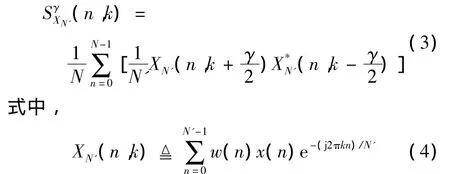
是对x(n)的离散傅里叶变换;w(n)是数据窗;k和γ分别表示频率和循环频率的离散间隔;N表示在观察时间内的总共离散采样数;N'表示在短时离散FFT 中的点数［8］。

TFAM对Frank码的循环谱密度估计结果如图1和图2所示，分别表示了在双频率平面的Frank码信号循环特征。通过分析这些特征与Frank码信号关键参数的对应关系，可以实现对关键参数的提取工作［9］。

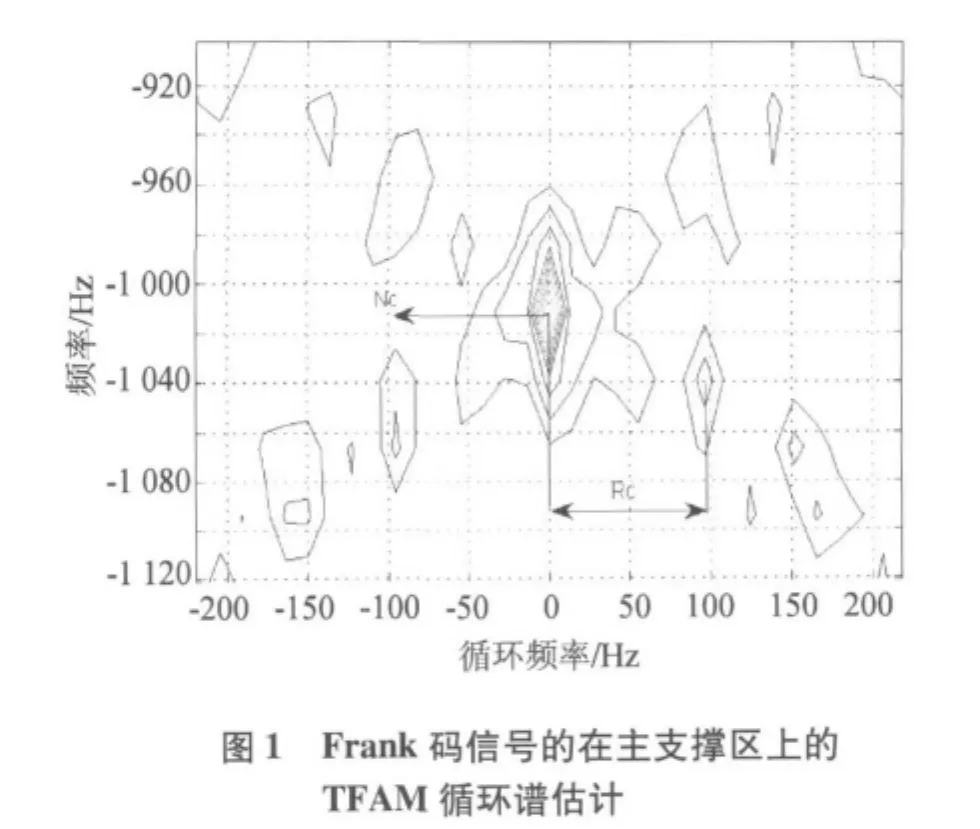
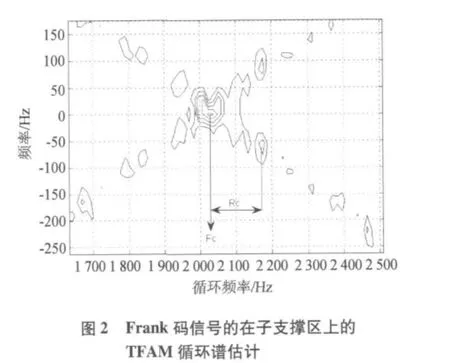
图1表示了对码长度Nc和码率Rc的提取:在循环频率为0处的主支撑区封闭曲线的条数与码长Nc对应，即Nc=9;然后通过测量主支撑区和循环频率2000 Hz处子支撑区峰值在循环频率轴上投影的距离来得到Rc。图2表示了对载频fc和码率Rc的提取:用同样的方法可以得到Rc，同时通过子支撑区峰值在循环频率轴上的投影值Fc得到载频fc，即fc=Fc/2。在得到Nc、Rc和fc的基础上，可以进一步计算得到更多的参数，具体将在下节讨论。

1.2 离散频率平滑FFT累积算法(DFSM)

在计算量上，直接频率平滑算法要优于Wigner-Ville分布等间接平滑算法。DFSM算法的基础由下面的离散频率平滑循环谱图表示［9］:是x(n)的离散傅里叶变换;w(n)是长度为N的矩形窗，是与总观察时间关联的FFT总点数;其他参数与式(2)和式(3)中的意义相同。

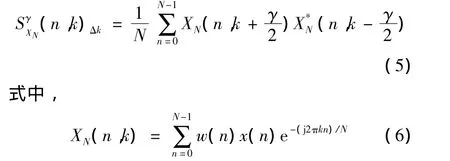
DFSM对Frank码的循环谱密度估计结果如图3所示，分别表示了在双频率平面的Frank码信号循环特征。可用与图1和图2同样的方法提取Nc、fc和Rc这3个重要参数。

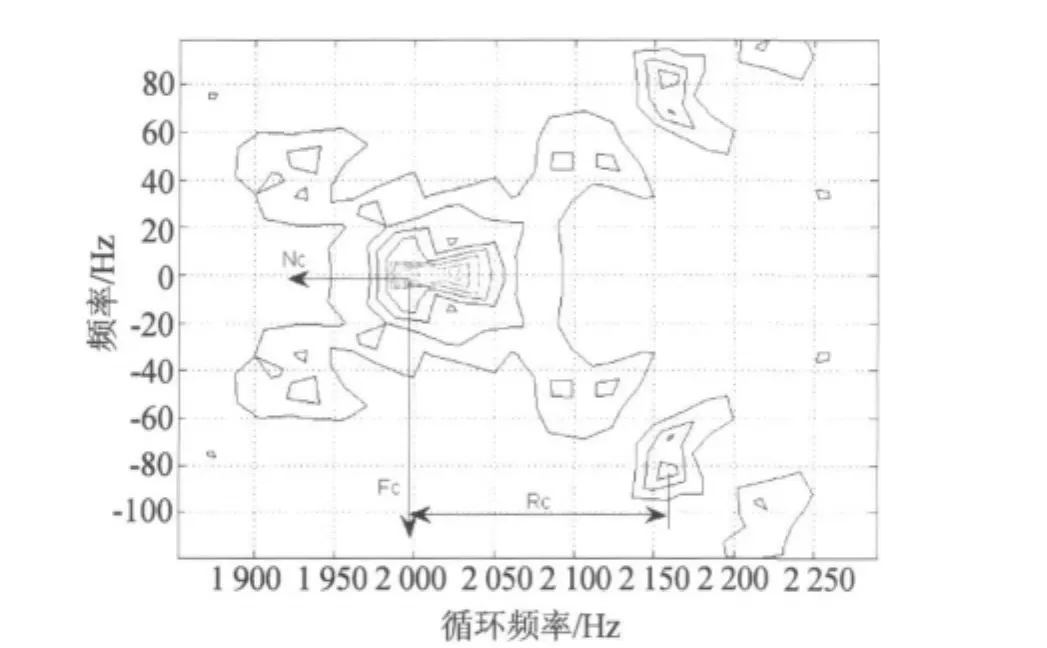
图3 Frank码信号的在子支撑区上的DFSM法循环谱估计结果

在双频率平面获得关键调制参数Nc，Rc和fc后，带宽B和编码周期tm也可以通过式(7)和式(8)的计算得到:

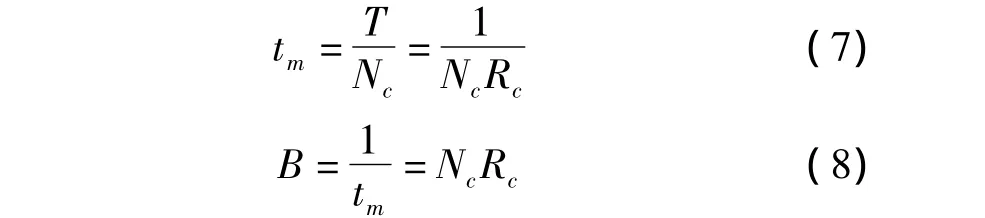
图1，图2和图3所表现的Frank码信号循环谱特征是在信噪比为－6 dB的高斯白噪声背景下得到的。上述对信号关键参数的提取效果体现了该方法对噪声具有很好的鲁棒性［10］，这是由于高斯白噪声作为平稳信号，在循环频率处不具有相关性，因此在循环谱特征分析中得到了很好的抑制。

2 基于循环谱特征分析的参数提取方法

在循环谱特征分析的基础上，进一步研究在无先验知识和参数未知［11］的情况下，对Frank码截获信号的关键参数提取方法，处理框图如图4所示。

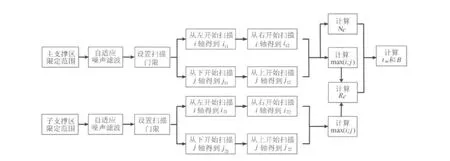
图4 双频率平面内循环谱特征分析方法对Frank码截获信号参数提取处理

首先对支撑区进行自适应滤波预处理，减少双频率平面的噪声影响并减少后续计算量。然后在双频率平面进行横向和纵向并行一维扫描，检测循环谱密度函数幅度峰值。扫描结果用于计算码率Rc和码长Nc，进而计算调制周期tm和带宽B。

Frank码截获信号的概率密度函数(PDF)的计算是通过并行扫描分别位于循环频率为0的主支撑和循环频率为2fc的子支撑区的i(水平)和j(垂直)轴，并记录门限以上的循环谱密度幅度值。i轴上的扫描可以得到:

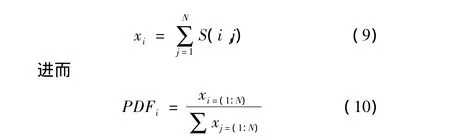
双频率平面上的循环谱密度分布可以确定支撑区的范围。在主支撑区，i和j轴的扫描从低值到高值(从左到右或从下到上)，以超过－6 dB的值开始，对应得到i11和j11，从高值到低值(从右到左或从上到下)，以低于－6 dB的值开始，对应得到 i12和j12。在子支撑区，通过同样的方式得到 i21，j21，i22和j22。因此

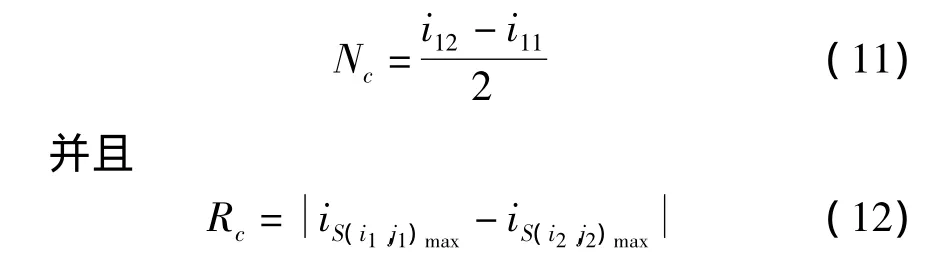
式中，iS(i1，j1)max表示主支撑区循环谱密度幅度峰值对应的i值;iS(i2，j2)max表示子支撑区循环谱密度峰值对应的i值。在信噪比较低的情况下，上述扫描方法会降低信号PDF。可采取自适应滤波［12］来确定对应的值。

3 方法验证

3.1 参数设置对循环谱特征分析的影响

以子码长度对频率分辨率的关系为例，说明参数设置对循环谱特征分析的影响效果。由于循环频率分辨率Δα和频率分辨率Δf要比测量或提取的最大参数小［13］，故要注意参数设置对频率分辨率的限制。当子码长度Nc分别取9和16时，对应的码元速率Rc分别为

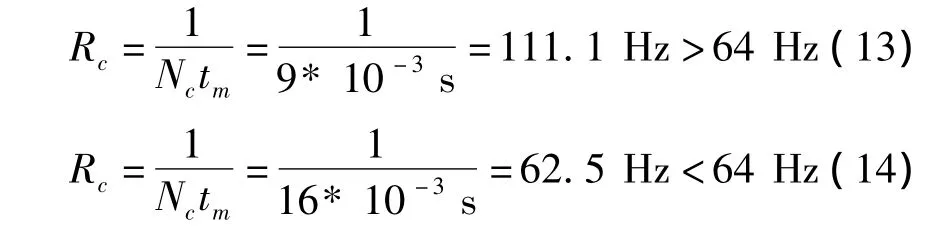
因此在 Nc≤9时，频率分辨率 Δf可以达到64 Hz;但Nc≥16时，频率分辨率达不到64 Hz，也无法得到码率。此时使用循环谱密度函数估计方法是，采用的频率分辨率要低于64 Hz，也就降低了循环谱特征分析的效果。

3.2 结果和结论

如果a*是真值a的测量值，则相对误差εr的绝对值定义为

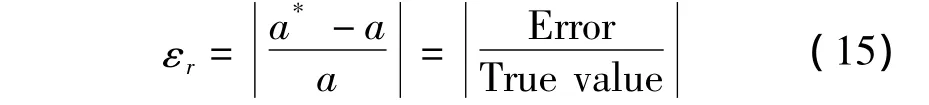
作为对参数提取效果的度量。

6个Frank码信号分别采用TFAM和DFSM方法进行参数提取［14］，参数分别为 fs，fc，B，Nc，结果分别见表1和表2，参数的真值和测量值如图5～7所示。

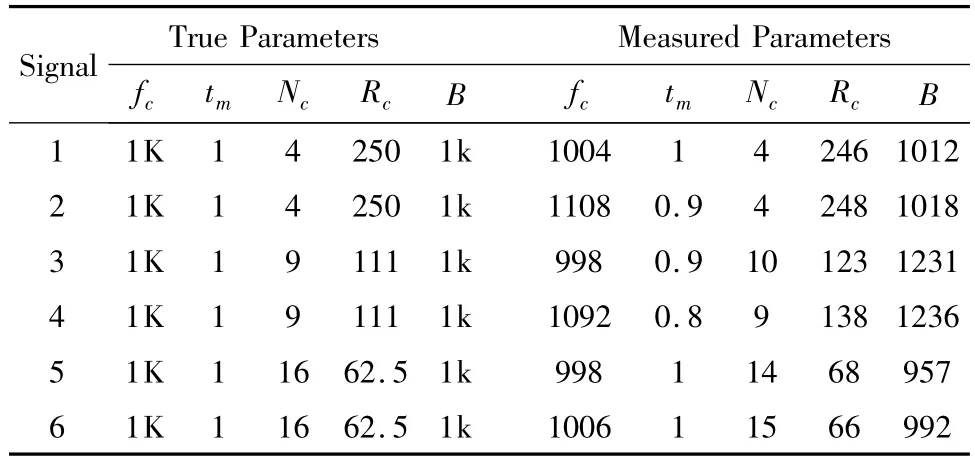
表1 信号参数和TFAM法估计结果

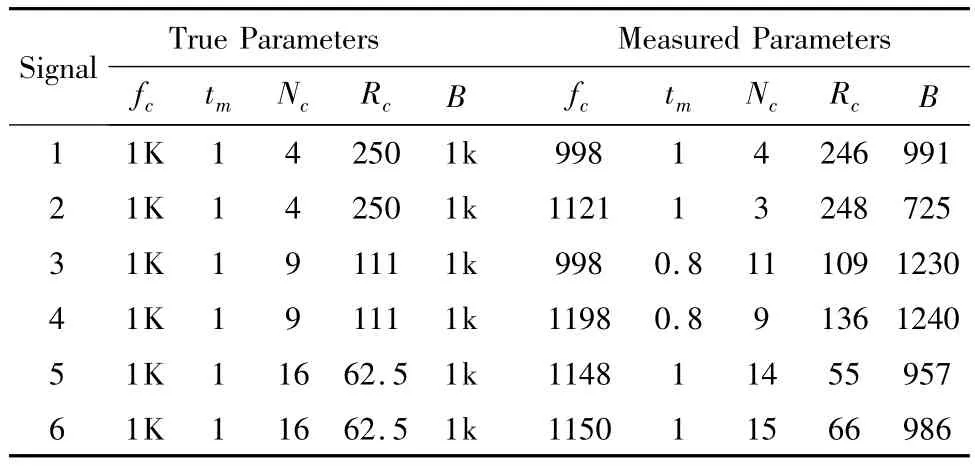
表2 信号参数和DSFM法估计结果

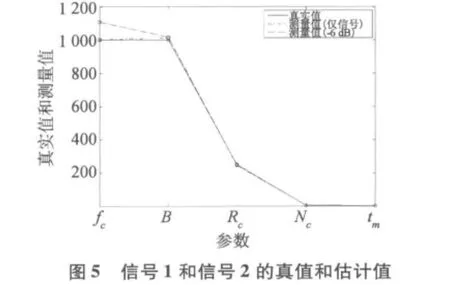
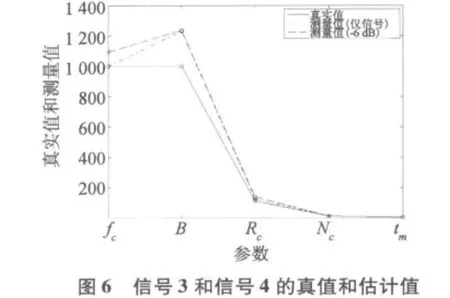
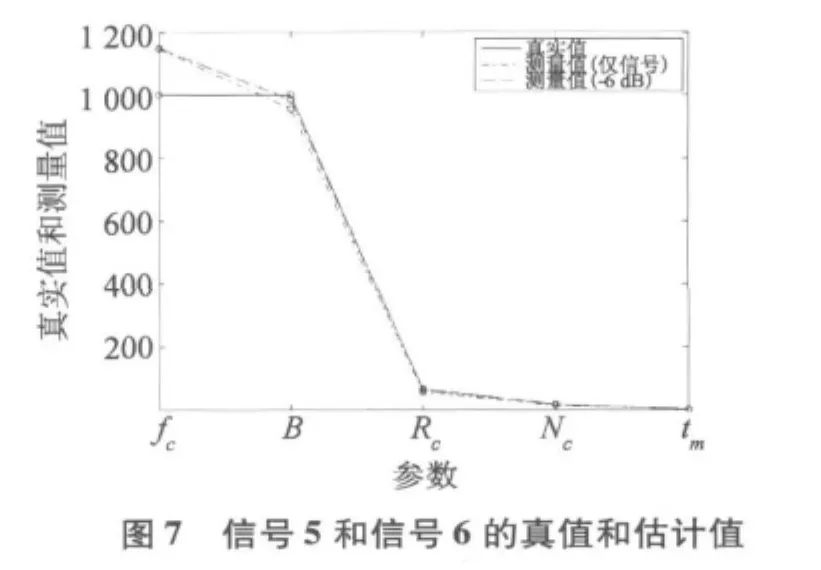
由验证结果看，载频fc和带宽B的相对误差在无噪声的背景下很小，但其相对误差受噪声的影响最明显;子码长度Nc和子码周期tm的相对误差受噪声的影响最不明显;码元速率Rc的相对误差取决于对tm和Nc的估计误差，还受到双频率平面内并行扫描的影响，综合结果较为复杂，最大相对误差发生在子码长度为9和16处。除Rc外，其他关键参数的相对误差趋势是误差随着子码长度的增大而减小。这是由于大的子码长度可获得大的处理增益。注意该提取算法的另一个显著优点除带宽B外，其他关键参数的相对误差对非循环平稳噪声不敏感，原因是非循环平稳噪声在循环频率处不具有相关性，在循环谱特征分析中得到显著抑制［15］。

4 结语

综上所述，循环谱特征分析信号参数提取方法具有不需要先验知识，对平稳噪声信号不敏感及对大子码长度信号处理增益大等良好性质，能较好的实现对Frank码截获信号参数进行提取。同时，大子码长度信号的码元速率Rc和低信噪比条件下的带宽B的参数提取效果，将是进一步研究和改进之处。

［1］PACE P E.Detecting and Classifying Low Probability of Intercept Radar［M］.Norwood，MA:Horizon House Artech，2004:41-65.

［2］SUTTON P D，NOLAN K E，DOYLE L E.Cyclostationary Signatures in Practical Cognitive Radio Applications［J］.IEEE Journal on Selected Areas in Communications，2008，26(1):13-24.

［3］张贤达，保铮.非平稳信号分析与处理［M］.北京:国防工业出版社，2001:357-360.

［4］徐海源，周一宇，黄知涛，等.一种Frank码脉压信号的检测与参数估计方法［J］.系统工程与电子技术，2007，29(6):24-27.

［5］GULUM T O，PACE P E.Extraction of Polyphase Radra Modulation Parameters Using a Wigner-Ville Distribution-Radon Transform［C］//IEEE International Conf.on A-coustics，Speech and Signal Processing，Las Vegas，NV，2008:1505-1508.

［6］GARDNER W A.Statistical Spectral Analysis:A Nonprobabilistic Theory［M］.NJ:Prentice-Hall，1987:43-69.

［7］ROBERTS R S，BROWN W A，LOOMIS H H Jr.Computationally Efficient Algorithms for Cyclic Spectral Analysis［M］.Signal Processing Magazine，IEEE，1991，8(2):38-49.

［8］汪赵华，陈昊，郭立.基于频域平滑循环周期图法的直接序列扩频信号的参数估计［J］.中国科学技术大学学报，2010，40(5):466-473.

［9］GARDNER W A.Signal Interception:A Unifying Theoretical Framework for Feature Detection［J］.IEEE Trans.on Communications，1988，36(8):897-906.

［10］ANTONIO F LIMA Jr.Analysis of Low Probability of Intercept Radar Signals Using Cyclostationary Processing［D］.Naval Postgraduate School Master's thesis，2002:78-90.

［11］余敬东，郭伟，李牧.直接序列扩频通信的循环谱检测和参数估计技术［J］.电子科技大学学报，1996，25(9):439-444.

［12］GULUM T O.Autonomous Nonlinear Classification of LPI Radar Signal Modulations［D］.Naval Postgraduate School Masters Thesis，2007:18-34.

［13］DOBRE O A，ABDI A，BAR-NESS Y，et al.Survey of Automatic Modulation Classification Techniques:Classical Approaches and New Trends［J］.Communications，IET，2007，1(2):137-156.

［14］DANDAWATE A V，GIANNAKIS G B.Asymptotic Theory of Mixed Time Averages and kth Order Cyclic Moments and Cumulant Statistics［J］.IEEE Trans.Inform.Theory，1995，41(1):216-232.

［15］NAPOLITANO A.On the Spectral Correlation Measurement of Non-stationary Stochastic Processes［C］//Conference Record of the Thirty-Fifth Asilomar Conference in Signals，Systems and Computers，2001:898-902.