飞机颤振模态参数的偏差补偿辅助变量辨识

王建宏， 王道波

(南京航空航天大学自动化学院，南京 210016)

0 引言

颤振是飞机非线性定常气动力和结构弹性力交互作用的结果。为避免颤振引起的灾难性后果，飞机试飞前需要在风洞中进行结构相似、刚度相似的模型颤振试验，然后在空中进行亚临界颤振试验。颤振辨识通常是在亚临界条件下试验，从试验数据辨识出气动弹性耦合系统的弯曲、扭转的频率和阻尼，并据此推算出颤振临界速度，进行颤振飞行边界预测，提供飞机的适航条件，为准确地对飞机进行控制器的设计提供前提条件。

文献［1］采用一种适用于噪声环境的广义整体最小二乘法，辨识飞机的颤振模态参数。但是广义整体最小二乘法的计算复杂度仍很大，并且由此所得的参数估计值具有较差的随机渐近性和有偏性。文献［2］利用频域子空间算法辨识模型参数，此时在频域辨识时需要保证输入和输出信号在观测时间区间内是周期信号，以保证在做离散傅里叶变换时不会产生混叠谱和泄露谱。另外利用线性的广义奇异值分解求解模型参数实质是利用奇异值截断的方法，将辨识的高阶系统近似表示为低阶系统，这会导致非主要模态辨识精度不高。文献［3］利用频域极大似然估计法(ML)辨识模型参数，但是极大似然估计的非线性损失函数需要借助于优化迭代算法求取极小值点，在噪声较大的情况下，迭代算法将有可能收敛到局部最小点。为解决上述问题，以及弥补该方法的不足，本文在颤振风洞实验时，针对输入和输出观测数据都被噪声污染的情况，对常规的偏差补偿最小二乘法进行改进，得到一种新颖的偏差补偿辅助变量辨识法。文献［1－3］中均假设输入和输出噪声为白噪声，而这种假设条件在实际的实验过程中是种理想状态，很难实现。本文将文献中的特殊情况推广为一般的情况——输出观测噪声为有色噪声。

1 问题描述

颤振试飞试验的随机模型如图1所示。

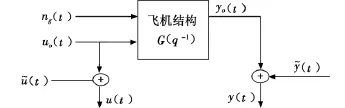
图1 颤振试飞试验中的随机模型Fig.1 Stochastic model of the flutter test experiment

图1中:u(t)和y(t)为包含各类噪声的输入和输出测量信号;u0(t)为对飞机结构施加的人工激励;ng(t)为大气紊流激励，由于飞行试验中不可避免地受到大气紊流激励的影响，作为一种不可测激励，它所产生的随机响应将作为过程噪声包含在测量的响应信号中;y0(t)为输出的振动加速度信号;(t)和(t)为传感器产生的测量噪声。飞行试验的激振采用火箭激振，激振点和传感器布置的原则是能有效地激励感兴趣的机翼一阶对称弯曲模态，一阶反对称弯曲模态和一阶对称扭转模态，并且能有效地测量这三阶模态所对应的响应信号。通过估计各种飞行状态的频率和阻尼随高度、速度的变化情况来确定飞机的颤振特性。在时域内有如下关系式成立

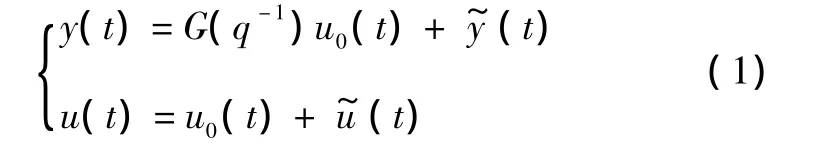
采用有理传递函数模型的飞机结构有

式中:ai和bi为多项式的系数;na和nb为多项式的阶数。定义pr(r=1，2，…，na)为上式中的传递函数的极点，则模态频率和阻尼系数可表示为

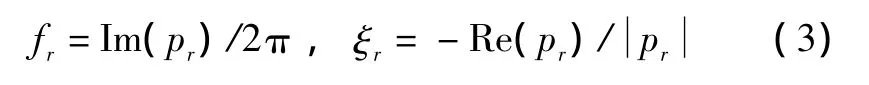
显然准确的传递函数估计是模态参数辨识的前提。

所考虑的一般条件假设为

假设1 A(q－1)的所有零点都在单位圆外并且A(q－1)和B(q－1)没有共同的公因子。

2 偏差补偿辅助变量辨识

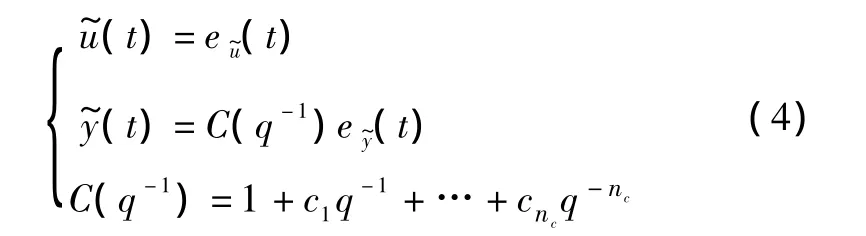
设

其中:θ0为真实的参数矢量;为待估计的模型参数矢量;φ(t)为观测信号的回归矢量，类似可定义噪声的回归矢量(t)。利用上述定义的矢量，可将式(1)改写为

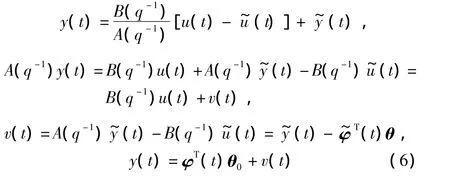
式中，v(t)表示随机扰动项。

为了简化书写，引进如下的符号表示

设一新的辅助变量z(t)∈Rnz(nz≥na+nb)，考虑如下的过参数系统

因为未知的模型参数矢量必须满足上式，经典的辅助变量估计值记为。

定义的辅助变量z(t)有时会满足第1个条件，但同时与第2个条件是矛盾的。当辅助变量中的延迟元素增加时会与回归矢量不相关。将偏差补偿辨识法与辅助变量法结合起来得到一种新颖的辨识方法－偏差补偿辅助变量法。该方法的第1步是根据有色输出噪声来构造辅助变量，第2步则利用偏差补偿法来消除由输入噪声所导致的偏差。允许由辅助变量法得到的参数估计值是有偏的，这极大地放松了式(9)中的两个条件，从而使得辅助变量的选择空间余度增大。

定义一个包含输入和延迟输出的辅助变量为

利用式(8)的结果可得到对应的辅助变量估计值为

假设有d≥na+nc，则通过简单的计算有

将式(12)代入到式(11)有

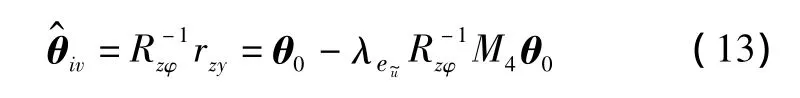
总之，国际商法项目课程教学模式是以职业标准为基础，以课程定位为前提，以课程目标为指南，以课程项目为载体，以课程设计为依托，以课程实施为途径，以课程评价为保障的“标准转换、理实一体”课程教学模式。该教学模式的七个环节环环相扣，递进展开。在第一轮教学过程结束时，课程评价的结果可以在下一轮教学活动中予以运用，实现循环优化。

从式(13)可见若输入噪声方差λeu～，可从辅助变量估计值中减去估计值的偏差得到关于模型参数的一致性估计矢量值为

定义残差r1为

取相关运算得:

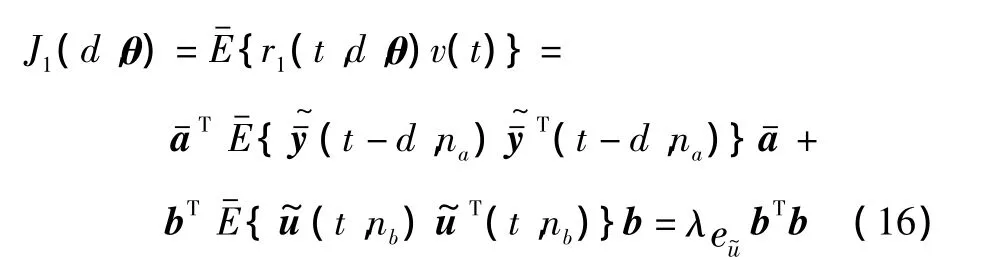
若b的估计值可获得，代入上式可进一步得到关于输入噪声方差λeu～的估计值为

在实际的运算过程中可将式 (17)与式(14)相互不断地迭代，以得到最终的一致性的参数估计矢量和一致性的输入噪声方差的估计值。因输入噪声方差λeu～的估计值依赖于参数矢量b，为了提高准确的估计值可采用对数据进行滤波的方法来改善估计值的统计性质。设一滑动平均的滤波器F(q－1)为

类似可定义对应的残差为

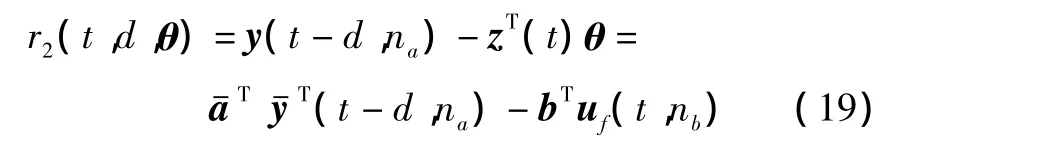
其中

取相关运算得:

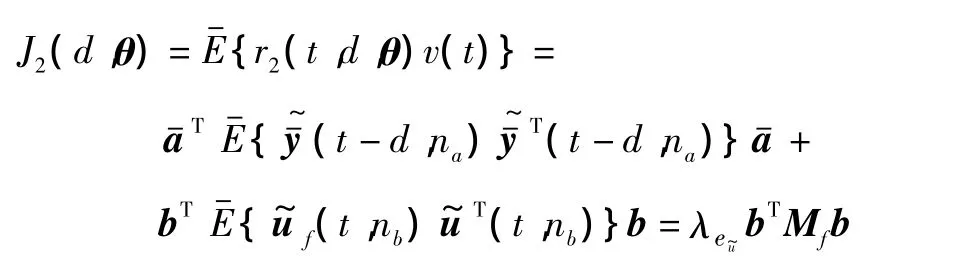
其中的Mf矩阵为如下的Toeplitz矩阵:

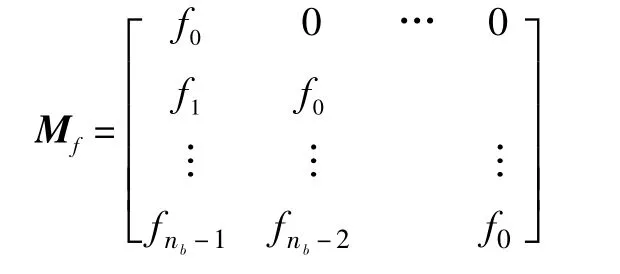
同样若b的估计值可获得，代入上式可进一步得到关于输入噪声方差λeu～的估计值为

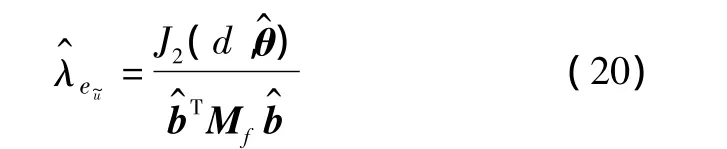
偏差补偿辅助变量法需要有关参数矢量θ的先验信息如初始值的合适设定，利用相互迭代的方法来得到最优的收敛值。将偏差补偿辅助变量法归纳如下:

考虑偏差补偿辅助变量辨识算法的一致性和准确性，假设若能得到方差值λeu～的一致性估计，根据偏差补偿法和辅助变量法中的相关结论可知:由偏差补偿辅助变量辨识算法计算出来的参数估计值也是一致性的。而方差值λeu～的一致性估计可由迭代算法中的模型参数的一致性估计的特性来保证。

3 仿真实例

以某型飞机的颤振试飞数据为例［8］，采用赫伯尔特(J.C.Houholt)建立的二维机翼的颤振数学模型，输入为人工施加的激励信号，输出是从测点集采集的加速度计测量，仿真是基于100次独立的实验，500个数据点。将本文的方法与常规的辅助变量法进行比较。

评价标准如下:

1)算法主体的计算时间(多次运行的平均时间，以s为单位);

真实系统为

白噪声的方差分别定义为λeu～=0.14和λey～=1.45以使得对应的输入－输出信号的信噪比(SNR)为10 dB。

其中，Px为信号x的平均功率。滤波器可选择为

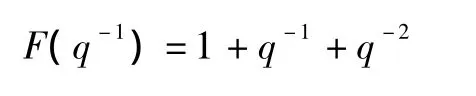
结果分析:对这个系统多次运行偏差补偿辅助变量算法和辅助变量算法(直到找到最优的参数值)相应的辨识结果见表1和表2，为简化符号记偏差补偿辅助变量法为BCIV，辅助变量法为IV。

表1 两算法性能比较Table 1 Comparison of the two algorithms’

表2 系统传递函数中的参数估计值比较Table 2 The estimated parameter values of the system’s transfer function

从表1和表2可看出:因BCIV是在IV的基础上得到的，它的估计性能结果优于IV，但由于BCIV算法需要解决优化问题，它的计算复杂度明显要比IV复杂得多。

因模态频率和阻尼系数可通过传递函数的极点求出来。为提高算法的效率，在线颤振分析时只需计算系统传递函数的极点，使用传递函数的极点作为比较标准，以验证算法的有效性。如图2所示，传递函数的真实极点与本文辨识方法所得到的极点值是非常一致的，再利用式(3)可计算出非常准确的模态参数值。为了验证分子多项式辨识的结果，将本文方法与经典辅助变量方法进行比较，图3给出了真实系统和本文辨识方法所得系统Bode plot之间的逼近程度。图4给出了真实系统和辅助变量方法所得系统的Bode plot。如图3所示，二者吻合得较好，如图4所示，在低频处两曲线有明显的分离误差，这表明在噪声环境下利用本文的辨识方法可获得与理论值相吻合的传递函数估计结果，进一步验证了本文算法的有效性。

图2 传递函数的真实极点和估计极点的比较Fig.2 Comparision of the true poles and estimated poles about the transfer function

图3 真实系统与估计系统Bode图之间的比较Fig.3 Comparision of the Bode Plot between the true system and estimated system

图4 真实系统与IV估计系统Bode图之间的比较Fig.4 Comparision of the Bode Plot between the true system and IV estimated system

4 结论

本文采用偏差补偿辅助变量辨识法，准确地辨识出飞机的颤振模态参数，同常规的辅助变量辨识算法相比，该算法采用相互迭代的方式来求解传递函数模型中的系数和噪声的方差值，解决了实验中常见的输入噪声为白噪声，输出噪声为有色噪声的情况。因本文算法融入了偏差补偿校正过程，这就使得辨识精度高，能够增强在线辨识的辨识精度。

［1］唐炜，史忠科，李洪超.飞机颤振模态参数辨识的频域广义整体最小二乘算法［J］.控制与决策，2006，21(7):726-729.

［2］王建宏，王道波，王志胜.基于遗忘因子算法的飞行器颤振模态参数辨识［J］.中国空间科学技术，2009，6(12):7-13.

［3］王建宏，王道波.机载稳定跟踪转台速率回路的内模H 无穷控制［J］.电光与控制，2010，18(1):20-24.

［4］王建宏，王道波，王志胜.多个未知时延的MISO系统的递推辨识［J］.控制与决策，2010，25(1):93-98.

［5］蔡金狮.飞行器系统辨识［M］.北京:宇航出版社，2007.

［6］PINTELON R.SCHOUKENS J.Frequency domain maximum likelihood estimation of linear dynamic errors-in-variables models［J］.Automatica，2007，43(2):621-630.

［7］PINTELON R.Frequency-domain subspace system identification using non-parameteric noise models［J］.Automatica，2002，38(8):1275-1311.

［8］SCUTER P N.Suboptimal estimation of the parameters of discrete systems in the presence of correlated noise［J］.Electron，1972，17(8):411-412.

［9］BEGHELLI S，GUIDORZI R P，SOVERINI V.The frish scheme in dynamic system identification［J］.Automatica，1990，326(8):171-176.

［10］孙隆和.网络信息环境中的飞机作战平台武器火力指挥控制系统［J］.电光与控制，2010，17(3):1-8.

［11］李向旭，张曾科，姜敏.两轴稳定平台的模糊－PID复合控制器设计与仿真［J］.电光与控制，2010，17(1):69-72.