基于田口方法在工序检查频率的确定
2011-07-04刘勤远
刘勤远
上海交通大学机械与动力工程学院,上海 200240
1 概述
现阶段,轴类产品的加工,其产品质量的稳定程度取决于设备精度、参数选择、材料优劣等多个方面,多数企业都会选择在加工过程中进行检查工作,也就是“工序检查”。这种检查往往都是管理人员根据经验来确定的,但缺乏理论依据,检查是否能在成本最低的情况下达到质量控制的效果?得不到明确的答复。
田口(Taguchi)方法对质量管理原则的一个很重要的出发点就是质量经济性,即从事质量改进工作要从经济效益最优化出发考虑改进措施[1]。其基本思想是, 以质量损失函数[2-3]。为工具谋求管理成本和产品质量的最佳平衡, 从而使总损失(管理成本+质量损失)为最小,来进行过程反馈控制系统的设计。
本文从质量损失函数出发,结合本公司轴类加工实际情况,为工序检查频率的确定提供了理论依据。
2 基于田口方法确定检查频率
为了能够对产品质量问题的工序进行有效的质量控制,本文将讨论对这种连续型质量事故的工序检查频率的确定。
通常,工序检查有时间迟滞。发现不良品时,工序已经恢复正常,这时考虑调节工序,不如利用不良品连续的特性采用巧妙的筛选办法。由于不良品具有连续性。按一定间隔(n)进行抽样检查时,若发现不良品,抽样点前后就都要检查,把不良品剔除;若检查为合格品,就任其流下去。如图1所示,Status A和B都能够将不合格品剔除而不流入后工序。
遇到Status C、D两种情况,不良品就会流入后工序,如果想要发现并剔除不良品,以减少衍生损失,就要缩短检查间隔(n),增加检查次数,则检查费相应增加。反之,将检查间隔(n)延长,这样做虽然可以省下检查费,但漏检的不良品损失却增加。考虑到经济性,就要得到最佳的检查间隔。
这种场合的损失函数为:

式中 : F=x-2+(x+2)e-x
x=n/m
n为检查间隔;m为不良品平均持续量,由于不良品具有连续性,所以假设m>5;B为每次检查费用;A为单位不良品漏到后工序的损失;v为单位不良品的处置费,p为工序平均不良品率。
要使损失函数(1)式的L最小,则有:

通过已知数据求出(2)式右边值,进而求出x值,根据x=n/m,即可求出最佳检查间隔n。
不设检查(即n=∞)时的损失额为:
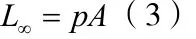
全数筛选(即n= 1)时损失额为:
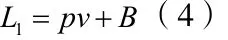
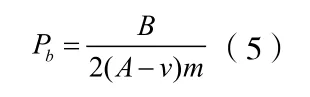
若实际不良率p小于Pb,则无需进行工序检查。通过分析:不良品的连续性越大,Pb就越小。
而经过抽样筛选后, 漏到下工序不良品率为K。

3 应用实例
本公司产品为轴类产品,由于设备较为陈旧,产品在加工外径是会由于抖动等的原因造成产品外径超差,但是经过长期加工得出经验,如果不进行任何修复作业,产品也会自动恢复到正常状态,一般情况下会有7个~12个连续的不合格品出现,也就是“连续型故障”,根据工厂长期经验和实验得到的数据,将参数设定如下。
我们以1件产品为单位产品,漏到后工序的损失A=11元(选别、拆装、延误等费用),B=5元/次,不良品的返修费用v= 3元,平均连续不合格品为m=10个,工序不良品率p=0.051。
第一步:用(5)式求工序临界不良品率Pb=0.0357。
因为 p=0.015>Pb,因此使用筛选检查。
第二步:用(2)式求最佳检查间隔,求得x=3.635,进一步求得n36。
第三步:按(1)式估算损失费,经过计算F=1.560,算的L=0.47。
第四步:按(6)式求漏到下工序的不良品率K=0.022。
通过比较,工序不良率为5.1%,通过优化的工序检查,漏到下工序去的不良率降低到2.2%,即剔除了2.9%的不良品,在改善上起到了作用。
第五步:损失比较。
如果全数筛选(n=1),显然损失太大,这种做法不经济,我们不予考虑。
而采用不检查,其的损失可以用(3)求得,L∞=0.561。
经过计算可知,通过抽样筛选检查,较不检查时单位产品可减少损失0.091元。
4 结论
本文从连续型质量事故的表现形式出发,从经济性的观点考虑,讨论了工序检查的不同方式,并且结合工厂的加工实际,进行应用。引入田口方法在线质量工程学,建立了质量损失函数,并且用实例展现了该方法可确实有效的降低损失(管理成本+质量损失),并且实施方便,最终将为工厂带来可观的经济增益,值得在工厂实施和推广。
[1]田口玄一.制造阶段的质量工程学[M].北京:兵器工业出版社,1992.
[2]韩之俊.质量工程学[M].北京:北京理工大学出版社,1991.
[3]朱立锋,薛跃,韩之俊.基于质量损失函数的仪器最佳校准周期的确定[J].电子工程师,2005,31(8):15-17.
