矩阵变换器开关损耗分析与计算

涂方明 王亚楠

（1. 海装驻武昌造船厂军代室，武汉430060; 2. 中国船舶重工集团公司第七一二研究所，武汉 430064）

1 引言

矩阵变换器（Matrix Converter）作为一种通用变频器具有人们所期望的多种优点，符合今后模块化发展方向[1-3]。图1为MC的基本结构，它主要由9个双向开关组成。双向开关的开关损耗分析是MC效率评估及系统设计的一个基本组成部分。由于MC的功率拓扑结构和调制策略与传统的电压源逆变器（VSI）大不相同，VSI的开关损耗分析不能适用于MC系统。对于MC系统，输入电压通过9个双向开关整合调制直接连到输出端，而不利用任何储能元件，这样便造成了IGBT模块截止时Vce电压不为恒值。即使输出电流为恒值时，由于输入电压区间的切换，各个IGBT模块的 c-e极电压和电流分配都是在变化的，各管的损耗也同时在变化，因此对MC的损耗分析必须从调制策略和IGBT模块的自身特性入手，研究各个开关模态下的开关损耗。国外对MC开关损耗的分析研究的较早，文献[4]将MC和VSI的开关损耗进行了比较，其损耗模型不够清晰，简单的得到了两个系统的仿真结果。文献[5]将每个开关周期内的线电压分为高、低两类，对双电压调制下 MC开关损耗进行了分析和计算，得到了双电压调制下传导损耗和开通、关断损耗的估算解析表达式，但是其开通和关断损耗的估算解析表达式并不能适用其它调制策略，影响了其通用性。

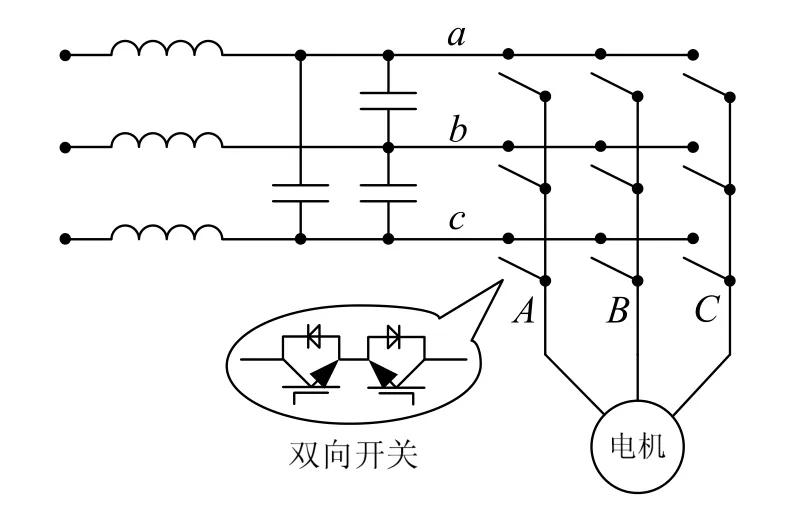
图1 MC原理图

本文针对上述文献的不足，以电压型换流法的各个开关模态为基础，分析了各个模态的传导损耗和各个模态之间转换时的开通和关断损耗，通过计算机累加仿真求得了MC总的开关损耗。由于调制策略对MC开通和关断损耗影响较大，本文就几种调制方法下的开关损耗进行了分析比较，得到了计算开通和关断损耗的通用算法和估算表达式。

2 传导损耗分析

2.1 IGBT的瞬时传导损耗

IGBT导通时的物理特性决定了 IGBT的传导损耗，其瞬时传导损耗可以表示为通态压降和通态电流的乘积，即：

其中 Vce为 IGBT集电极-发射极电压，Ic为集电极电流。

而通常IGBT的伏安特性可由（2）式表示，其中Vceo为IGBT阈值电压，Rk为通态等效电阻。

式（2）代入式（1）得：

2.2 电力二极管的瞬时传导损耗

同样，电力二极管的瞬时传导损耗也可以表示为其通态压降和通态电流的乘积，即：

其中VAK为通态压降，Ic为通态电流。

而电力二极管的伏安特性可由（4）式表示，其中 VD0为二极管阈值电压，RDk为通态等效电阻。

将式（4）代入式（3）得：

2.3 MC传导损耗分析

因为MC的结构三相对称，现只对其一相进行分析，由于MC的负载一般为感性，一个开关周期内负载可以作电流源处理，负载电流可以看作近似不变。根据 MC的调制策略不同，每个开关周期内的状态变化顺序也不尽相同，假设一个开关周期内某输出相接入到输入相有k个状态，由图2可知每个状态总有也只有一个IGBT和一个二极管导通。

由于一个开关周期内开关切换的时间很短，次数也有限（只有k次），其间的传导损耗相对整个开关周期传导损耗很小，可以忽略，传导损耗不受调制策略影响，所以一个开关周期内的传导损耗应为IGBT和电力二极管传导损耗之和：

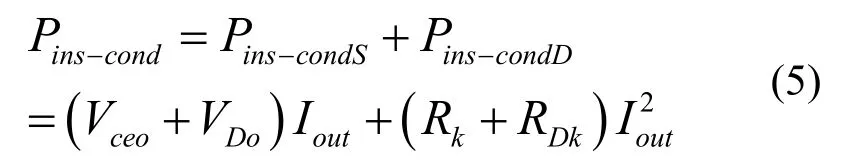
图3为 MC运行时的瞬时传导损耗仿真波形，传导损耗为与输出频率ωo有关的周期函数，由式（5）可求得MC单相平均传导损耗为：

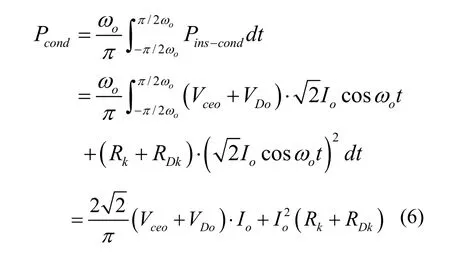
3 MC开通和关断损耗分析

3.1 以输入电压区间划分的各个开关模态

通常IGBT的开通和关断损耗为其通态电流和断态c-e极端电压乘积的函数。硬开关模式下，单管单次开通损耗和关断损耗分别为：

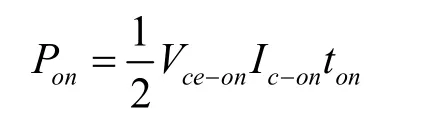
式中：Vce-on为开通前电压，Ice-on为开通后电流。

式中：Vce-off为关断后电压，Ic-off为关断前电流。

图2 MC单个开关周期内的状态

图3 MC瞬时传导损耗仿真波形

由图 2可知，输入两相之间进行换流时，IGBT的c-e极端电压与输入相有直接联系，因此有必要按输入电压对各个开关模态进行划分。以线电压零点为界将输入电压周期划分为 6个扇区，每个扇区中各相电压的特点是一相为正极性，记为 VP，一相电压为负极性，记为 VN，另一相为VM，可得VP＞VM＞VN。通过划分，在每个扇区内可以将输入ABC相映射为PMN相，并按照电压高低排列，便于分析开通和关断的过程，如表1所示（以Iout＞0为例）。

3.2 开通和关断损耗模型

以输出电流大于零，采用电压型换流法由 P相换流到M相为例：P相导通时，SP1和DP2流过电流Iout，SM1预导通，DM2上承受VM—VP的反电压，经过两步换流法SP1硬关断，SM2软开通换流至M相，SM1流过电流Iout，SP1上承受VM—VP的电压。其间只有 SP1产生关断损耗如图4所示，ton、toff为开通和关断时间。同理可以分析 M 相到 N相、N相到P相等状态的换流损耗，得到各状态变换时的开通和关断损耗如表2所示。

图4 电压型换流过程分析

3.3 Venturini法的开通和关断损耗

利用表2得到的开通和关断损耗模型可对整个MC进行仿真，图5为采用Venturini法输出频率为 20Hz时瞬时开通损耗（黑影由损耗脉冲序列构成）。由图可知，瞬时开通损耗受输出电流频率ωo的调制，但不是周期可积函数，不易得到像传导损耗那样的总损耗通用表达式。

图5 采用Venturini法，输出频率为20 Hz时瞬时开通损耗

观察表2可知，各状态变换时的开通和关断损耗与输入线电压和输出电流有关，为了便于分析，先只分析输入线电压对开通和关断损耗的影响，再加入输出电流的影响。图6为采用Venturini法时各管的开通电压波形，仿真结果显示开通电压不受输出电压及频率的影响，图6（a）中各管的开通电压只受输入线电压的影响，为总共6个半波的脉冲序列，开通时总平均电压为：

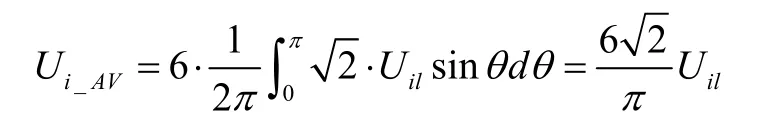
其中Uil为输入线电压有效值。

而输出平均电流为：

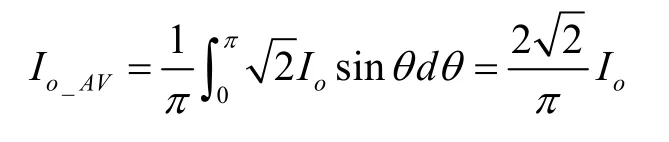
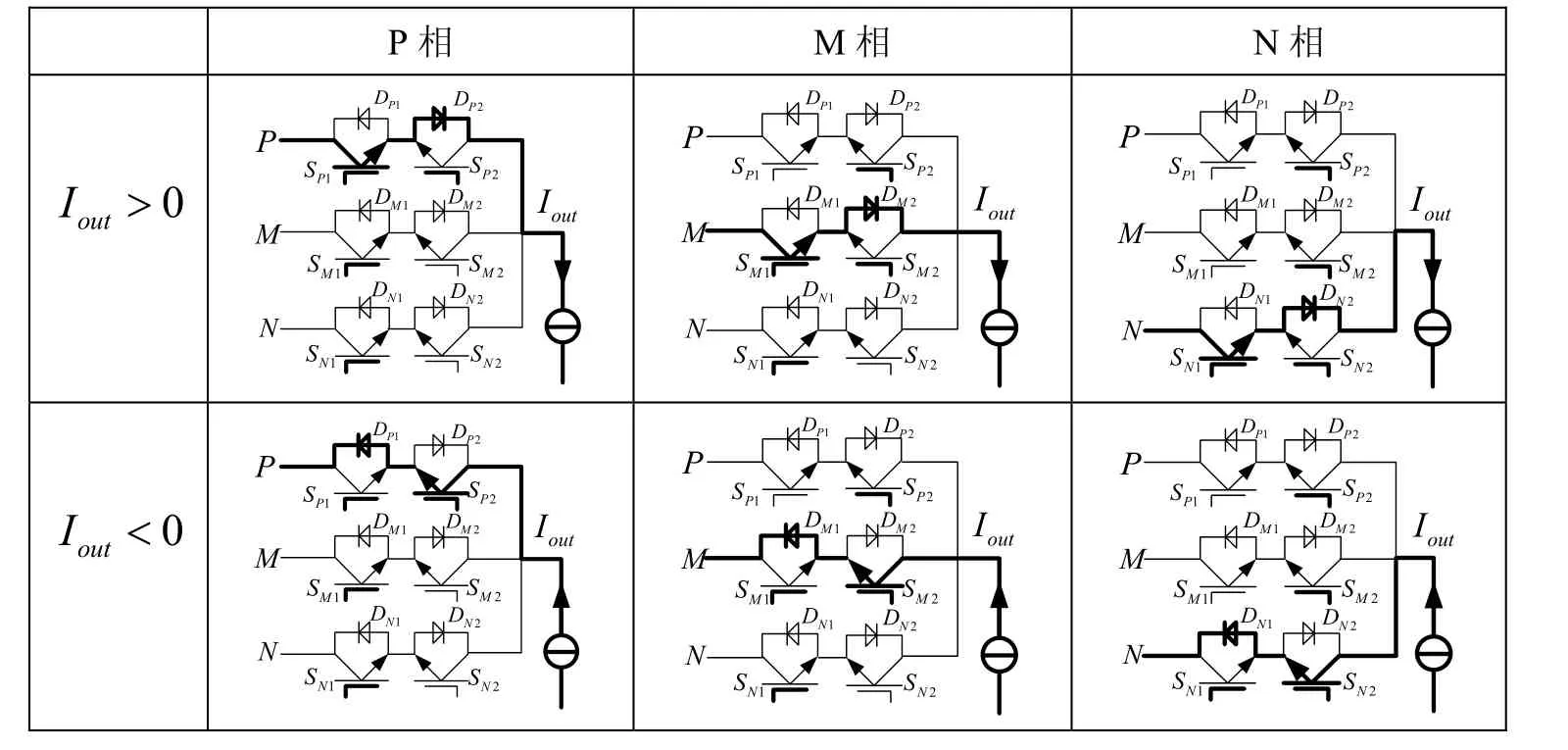
表1 以输入电压区间划分的各个开关模态

表2 各模态换流开通和关断损耗

其中IO为输出电流有效值。

则单相输出时的总开通损耗为：

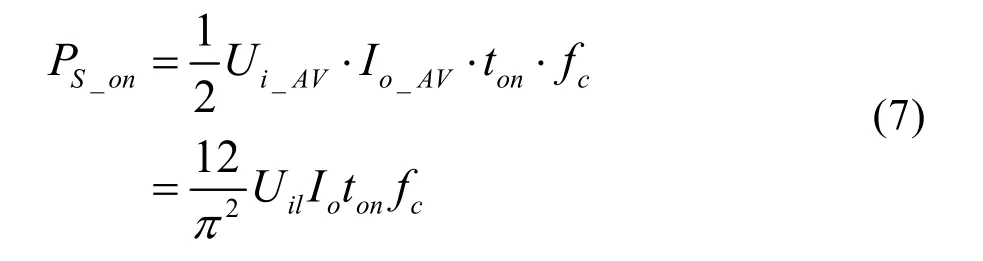
其中fc为开关频率。

各管开通损耗为：

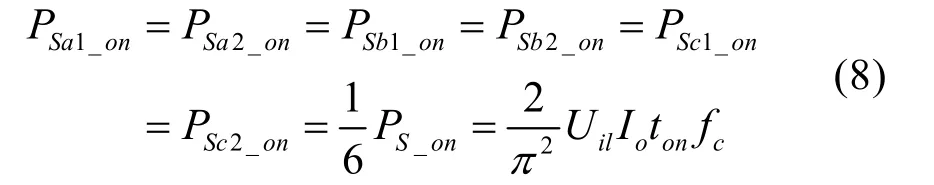
若将普通Venturini法单个周期内的开关顺序按图6（b）进行优化，从仿真结果可以看出a、b两相的开通损耗会减小50%，c相保持不变，总开通损耗是普通Venturini法的2/3。这是因为当A相输出时，原来的开关顺序是acbabc，现在变成aacbbc，a、b相的开通次数各减少了一次；当B或C相输出时，a、b相的开通次数同样会各减少一次。就单相输出而言，各管的开通损耗由于调制策略的不同会呈现不平衡的现象。

这时开通时总平均电压为：

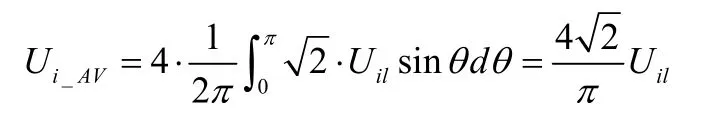
则单相输出时的总开通损耗为：

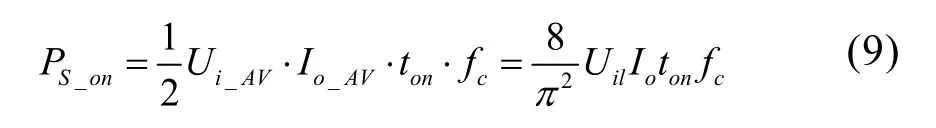
各管开通损耗为：

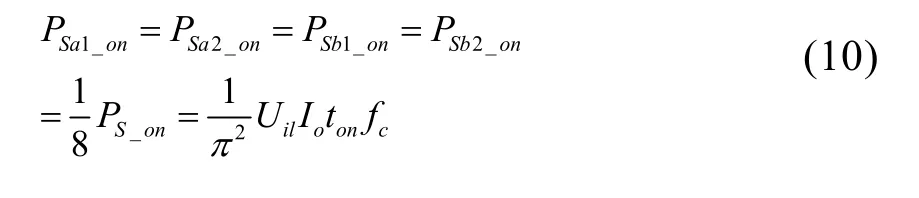
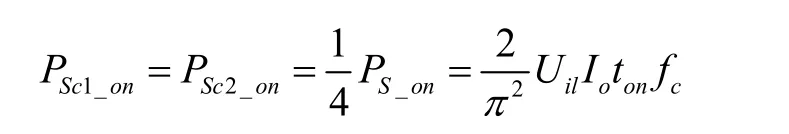
同理可以分析Venturini法的关断损耗，结论类似，但上述方法并不能推广到其它一般情况，例如空间矢量调制法，图7为采用空间矢量调制法，输出频率为20 Hz时的开通电压波形，其中各管的开通电压不仅受输入线电压的影响，而且还受输出频率的影响，波形近乎不规则，这与空间矢量法的调制方法有关。和Venturini法的每个开关周期都是固定顺序的旋转矢量不同的是，空间矢量法是通过输入电流和输出电压区间的组合有选择的挑选静止矢量，区间的不同导致了开通电压选择输入线电压的不同，所以空间矢量调制法很难得到开通时的总平均电压解析表达式，单管也是，只能通过仿真得到近似的数值解。

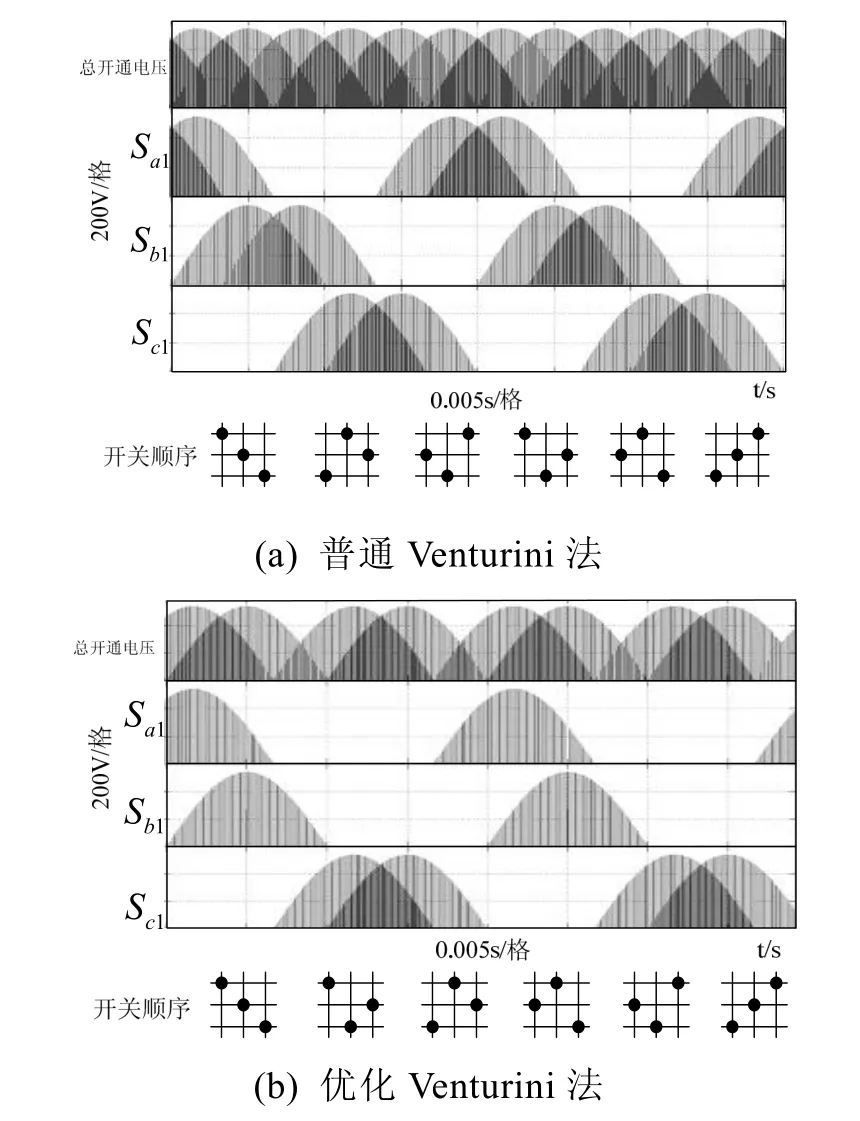
图6 采用Venturini法时各管的开通电压波形

表3为四种调制方法下的开通损耗系数，其中优化空间矢量法通过调整普通空间矢量法每个开关周期内的矢量顺序使得每次换流只开关一次。从表3可以看出，与Venturini法开通损耗系数不随输出频率变化不同，空间矢量法的开通损耗系数随输出频率增加而略有增长，但是同条件下，空间矢量调制法的开通损耗还是明显小于Venturini法（Venturini法的每个开关周期有6次状态，空间矢量法采用对称调制有9次）。

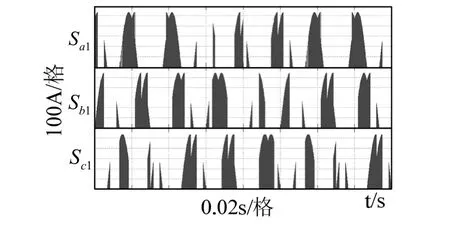
图7 采用空间矢量调制法，输出频率为20 Hz时的开通电压波形

由此，并不是所有的调制方法都能得到开通和关断损耗的解析表达式，调制方法的不同，总体、各管的开通和关断损耗也大不相同，只有在特殊的情况下（如Venturini法）才能得到精确的解析解，大多数调制方法的开通和关断损耗必须针对其调制过程进行仿真累加计算。

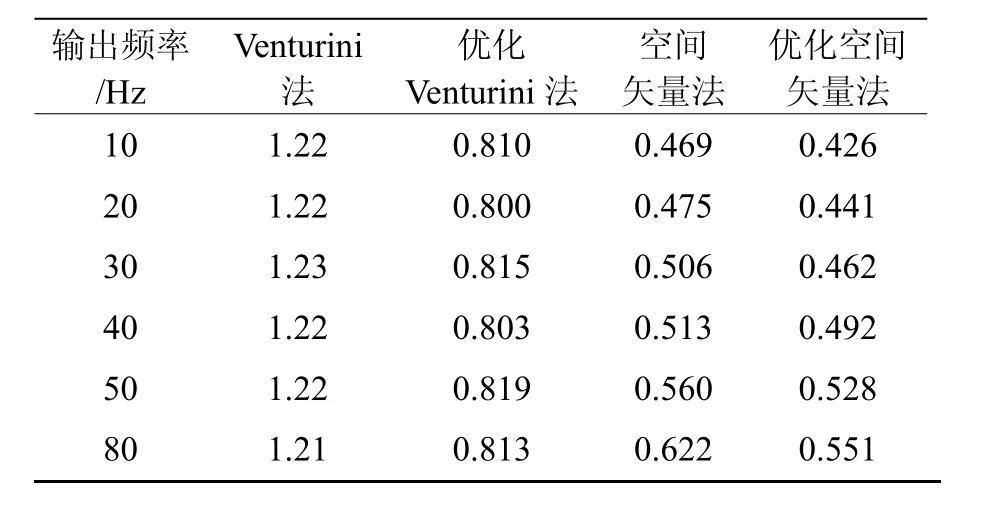
表3 四种调制方法的开通损耗系数（10 kHz）

图8为不同开关频率、不同调制方法下开关损耗，可以看出开关频率和调制方法对传导损耗没有什么影响，而对开通和关断损耗很大。比较四种调制方法，优化空间矢量法的总体开关损耗最小，Venturini法最大。

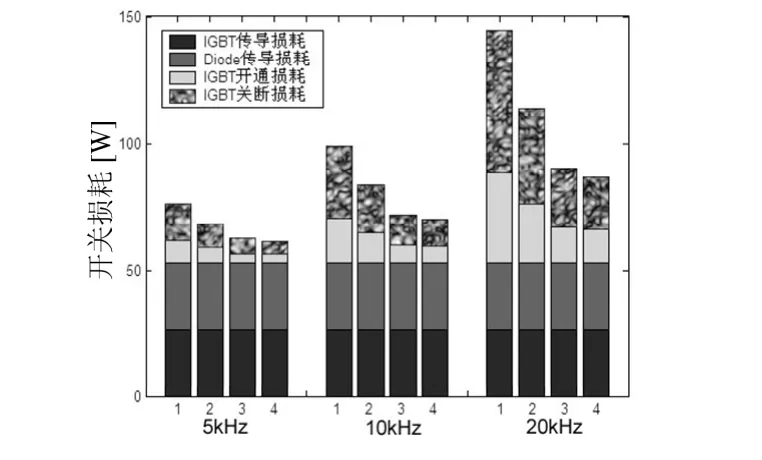
图8 开关频率对损耗的影响

4 结论

本文通过计算机累加仿真的方法对矩阵变换器的开关损耗进行了分析和计算，就几种调制方法下的开关损耗进行了分析比较，给出了计算传导损耗、开通和关断损耗的具体通用算法。仿真可知传导损耗为与输出频率ωo有关的周期函数；不同的调制方法、开关频率对开通和关断损耗的影响很大，对传导损耗几乎没有影响。

目前，双向开关由 IGBT和快速恢复二极管以共集电极或共发射极组合构成，随着大功率MOS、IGBT技术的日臻成熟，新型的开关器件将会被采用，现在已经开始出现RB-IGBT器件和整合模块技术应用于 MC，相信不久的将来会成为主流采用的双向开关，本文所阐述的开关损耗方法虽然是基于IGBT模块反串联的结构，但是其分析方法仍可以推广到其它器件模型。

[1]Wheeler P W, Rodriguez J, Clare J. Matrix converters：a technology review[J]. IEEE Trans. on Industrial Electronics, 2002, 49(2)：276-288.

[2]Blaabjerg F, Casadei D, Klumpner C. Comparison of two current modulation strategies for matrix converters under unbalanced input voltage conditions[J]. IEEE Trans. on Industrial Electronics,2002, 49(2)： 289-296.

[3]Lars Helle, Kim B Larsen, Blaabjerg F. Evaluation of modulation schemes for three-phase to three-phase matrix converters[J]. IEEE Trans. on Industry Electronics, 2004, 51(1)：158-171.

[4]Apap M, Clare J C, Wheeler P W. Comparison of losses in matrix converters and voltage source inverters[C]. IEE Seminar on Matrix Converters, 2003,4： 1-6.

[5]Kang Jun-Koo, Hara H, Yamamoto E. Analysis and evaluation of bi-directional power switch losses for matrix converter drive[C]. 7th IAS Annual Meeting,2002, 1：438-443.