多Agent粒子群算法在船舶电力网络重构中的应用

刘大宝 夏立 王征

（海军工程大学 电气信息与工程学院，武汉430033）

随着电力系统的工业化、智能化发展，同陆地电网类似，船舶电力系统安全运行面临着许多新问题新挑战，而其网络重构就是其中一个重要的热点研究问题。

由于船舶电力系统与陆地电力系统在分布格局、供电设备、供电需求等方面有很大的不同，船舶电力系统电力线路短，馈线单元多，电路电压比大，具备发电、配电甚至变电等一体环节，大多数情况下为环形网供电结构，因此在船舶电力系统分析时，各种方法应结合其供电特点而适时改进。目前，各种智能算法在网络重构求解中得到了较为广泛的应用。然而，模拟退火算法可以得到与初始解无关的全局最优解或次优解，但是其收敛速度慢，收敛性依赖于退火方案的选择；紧急搜索算法因记忆功能灵活能够避免陷入局部最优，但对初始值依赖性较强，搜索效率较低；蚁群算法[1]因正反馈、分布式计算与富于建设性的贪婪启发式搜索更快收敛到全局最优解，但其决定于转换概率的计算结果，容易陷入局部最优。

针对上述问题，本文在船舶电力系统的基础上，建立多Agent模型，进行拓扑分析，结合二进制粒子群算法思想对网络重构进行研究，并对仿真结果进行比较，验证这种算法的可行性。

1 船舶电力系统网络拓扑与数学模型

1.1 船舶电力系统网络拓扑结构分析

船舶电力系统中供配电系统多是集中配置，集发电、变电、配电与输电于一体[2]。如图1所示船舶电力系统中发电机组构成环形供电方式，各段主母线又形成了相对独立的辐射状配电网络，连接各种负载[3]。船舶负载一般分为三级：一级负载即最重要负载；二级负载是较重要负载；三级负载为非重要负载。其中重要负载又配置了备用路径供电，以提高供电的可靠性和安全性。

另外，图1表现的是节点-支路拓扑图，是运用图论的方法将电力设备（发电机、电动机、馈线等）抽象为支路，而设备之间的连接点抽象为节点。其中节点和支路按照图论中深度优先搜索和广度优先搜索原则进行编号，即包含在圆圈中的数字0～51表示支路编号，包含在正方形中的数字0～15表示节点编号。于是整个系统是通过跨接线将各电站进行统一起来的。

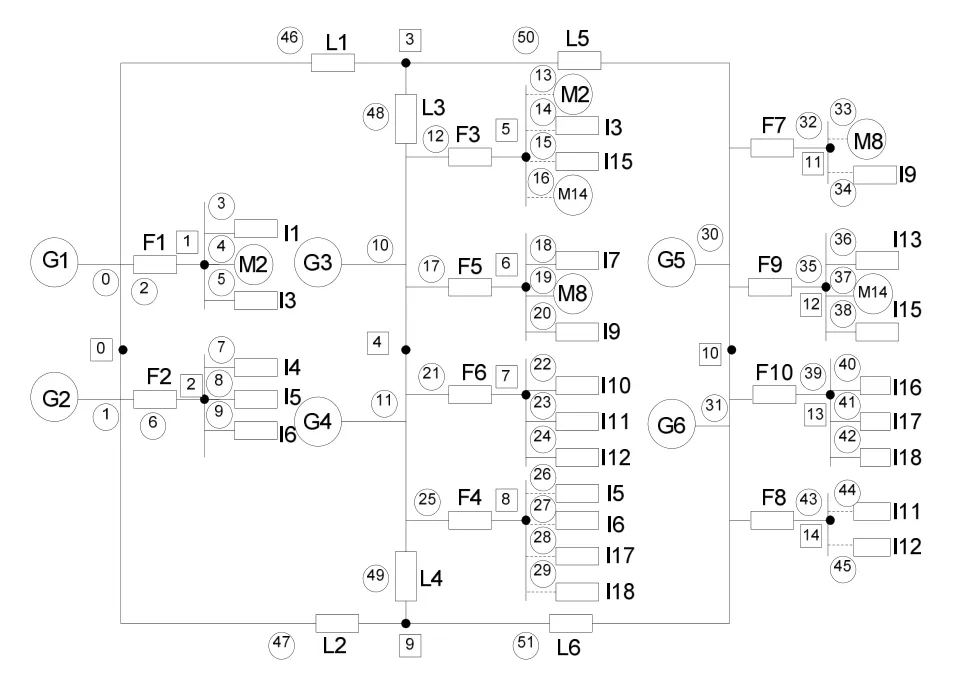
图1 节点-支路描述的舰船电力系统简化结构图

1.2 船舶电力系统网络重构数学模型

船舶电力系统网络重构目标就是遇到设备故障或者线路检修时，在满足操作条件与电气约束，通过改变网络结构中开关和设备状态尽可能多地将停电区域的负荷转移到正常的馈线上，以使配电系统中某个或某几个目标最佳。本文以最大恢复供电和最少开关切换次数为目标，其数学模型可以描述如公式(1)：

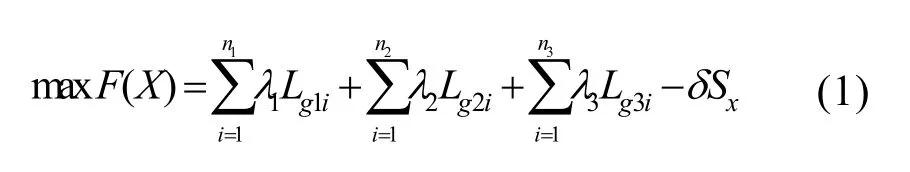
式中， Lg1i, Lg2j, Lg3f分别表示为三级负载，分别表示为要恢复的各级负载总数，是各级负载的重要性权重系数， Sx是某个恢复方案中开关操作总数，δ是其惩罚性权重系数。一般地，一级负载赋值λ1=1，二级负载赋值λ2=0.1，三级负载赋值λ3= 0 .01。如此就可以得到故障恢复中的评价函数即适应度函数。

服从以下约束：

其中：A―节点-支路关联矩阵；P―馈线潮流矢量；D―负荷需求矢量。

(4)辐射性约束：对恢复供电的重要负载，正常供电路径与备用路径有且仅有一条连通。

(5)优先级约束：按照负载优先级别高低逐次恢复供电。

2 基于多Agent粒子群船舶电力网络重构方法

2.1 多Agent技术在船舶电力系统中的应用

一般来说，Agent就是处于某个环境中具有主动行为能力的实体，如生物体、软件系统以及控制器系统等。多 Agent系统[5]是将多个结构和功能相对简单、容易实现的Agent组合起来，各个Agent在物理上或逻辑上是分散的，其行为是自治的，其自身的目标和行为不受其它Agent成员的限制，它们为了共同完成某项任务或达到某些目的，通过交换与合作解决超出单个Agent能力的问题。

船舶电力系统的拓扑结构为多电源多分段多联络辐射网。基于多Agent的区域自治特性，把区域馈线支路上由开关设备整体控制的非开关设备的集合当作一个Agent区段。因此，复杂的电力网络可以进行动态拓扑逻辑等效解耦及分区，分解成辐射状的独立供电单位 Agent。基于图 1的电力网络拓扑图以馈线为单位划分为各个子系统，每条馈线抽象为一个相应的馈线 Agent，得到区域馈线多Agent网络拓扑模型，如图2所示。

文中所述的区域馈线 Agent是一种智能Agent，具有复杂的决策判断能力，拥有知识能够自治，可以根据本区域馈线和相邻馈线的运行状况，通过和相邻区域馈线Agent信息交互，更好地保证电力系统稳定运行。

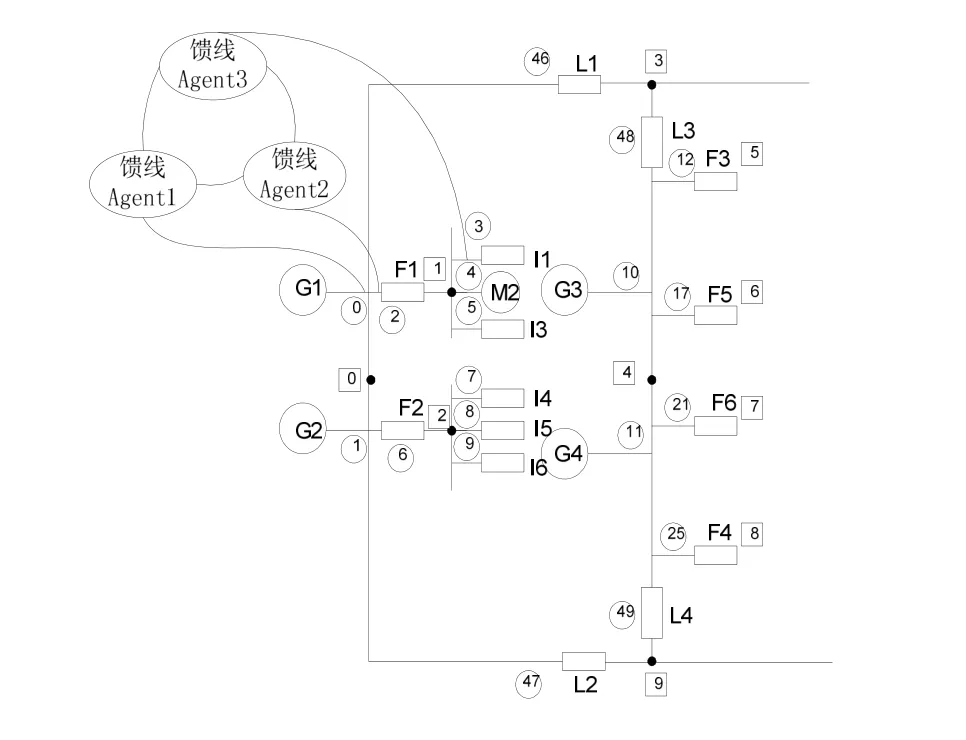
图2 船舶电力系统区域馈线Agent模型

2.2 二进制粒子群算法

在粒子群算法中，粒子的位置表示待优化问题的解，粒子的速度矢量决定了粒子的飞行方向和速率大小。设在一个M维的搜索空间，粒子i的位置信息可表示为 Xi=(xi1, xi2, …, xin,)，速度信息表示为Vi=(vi1, vi2, …, vin,)；粒子i经历的最好位置信息为Pi=(pi1, pi2, …, pin,)，也就是粒子i经历过的最佳适应度位置。假设f(x)为目标函数，微粒i的最好位置Pi由下面的公式确定[4]：

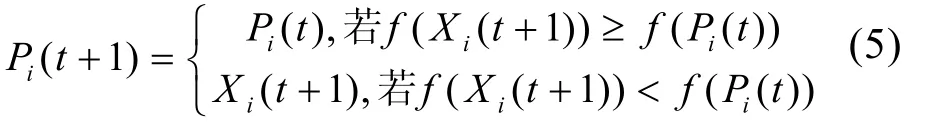
若种群中的微粒数是s，群体中所有的微粒所经过最好的位置即全局最好位置Pg(t)，则

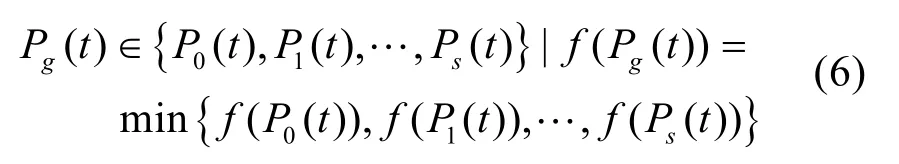
由公式(6)，可以得到粒子群算法的改进公式

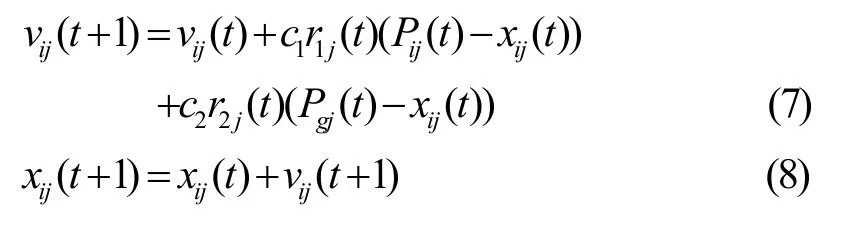
其中， j表示的是微粒的第 j维， i表示微粒i，t表示代数t，1c、2c为学习因子，视具体情况而定，1r、2r为取值在区间[0，1]上的随机函数。

二进制粒子群算法中，将粒子每一维位置和粒子的最佳位置个体都定位0或者1，也就是说只需要考虑粒子的速度，则引入了速度公式，即sigmoid函数，

粒子的速度值越大，Sigmoid函数越接近于1，然而，当速度越小，Sigmoid函数的接近于0。如此，可以把Sigmoid粒子速度函数值看成粒子位置是1或者是0的概率。

另外，考虑不使Sigmoid函数饱和，Sigmoid函数作如下调整：

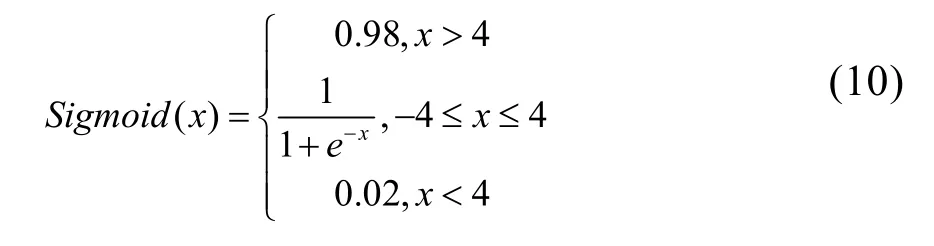
迭代过程中，ijx的计算公式为

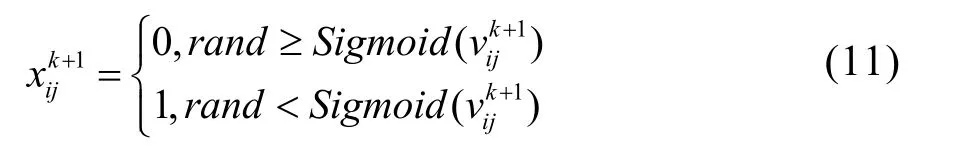
式中：rand是区间[0，1]的随机数。

2.3 多Agent粒子群算法

多Agent粒子群算法是基于二进制粒子群与多Agent的自治学习、彼此竞争以及相互协作操作机制的一种智能算法。根据船舶电力系统模型构造相应的区域馈线多Agent网络拓扑模型和定义每个Agent单元。通过Agent独立自治和与邻域Agent交互操作，吸收粒子群算法的进化机制，按照规则不断更新粒子群，使其能够更快、更精确地收敛到全局最优解。

在多Agent粒子群算法中，每个馈线Agent单元相当于一个粒子。粒子群的拓扑结构为群体中所有粒子之间相互连接的方式，即为船舶电力系统网络重构模型所决定。通过发挥Agent的自治特性与环境交互，并与邻域Agent进行协作，不断更新自身信息，完成问题求解。所以Agent粒子单元就是在满足运行约束条件的情况下，尽可能满足优化目标函数值。基于多Agent粒子群船舶电力系统网路重构的流程图如图3所示。

3 算例分析

通过对典型的算例进行分析，验证算法的可行性与可靠性。算例中数据来源是基于图1的数学模型，属性G表示发电机、M表示动态负载电动机、I表示静态负载、F表示馈线、L表示跨接线。具体参数均归化为标幺值，如表1所示。

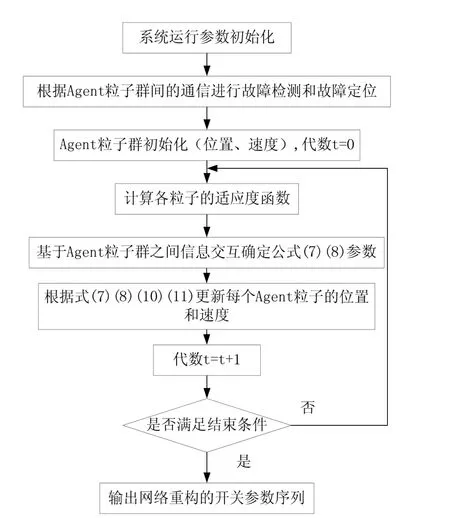
图3 基于多Agent粒子群船舶电力系统网络重构流程图

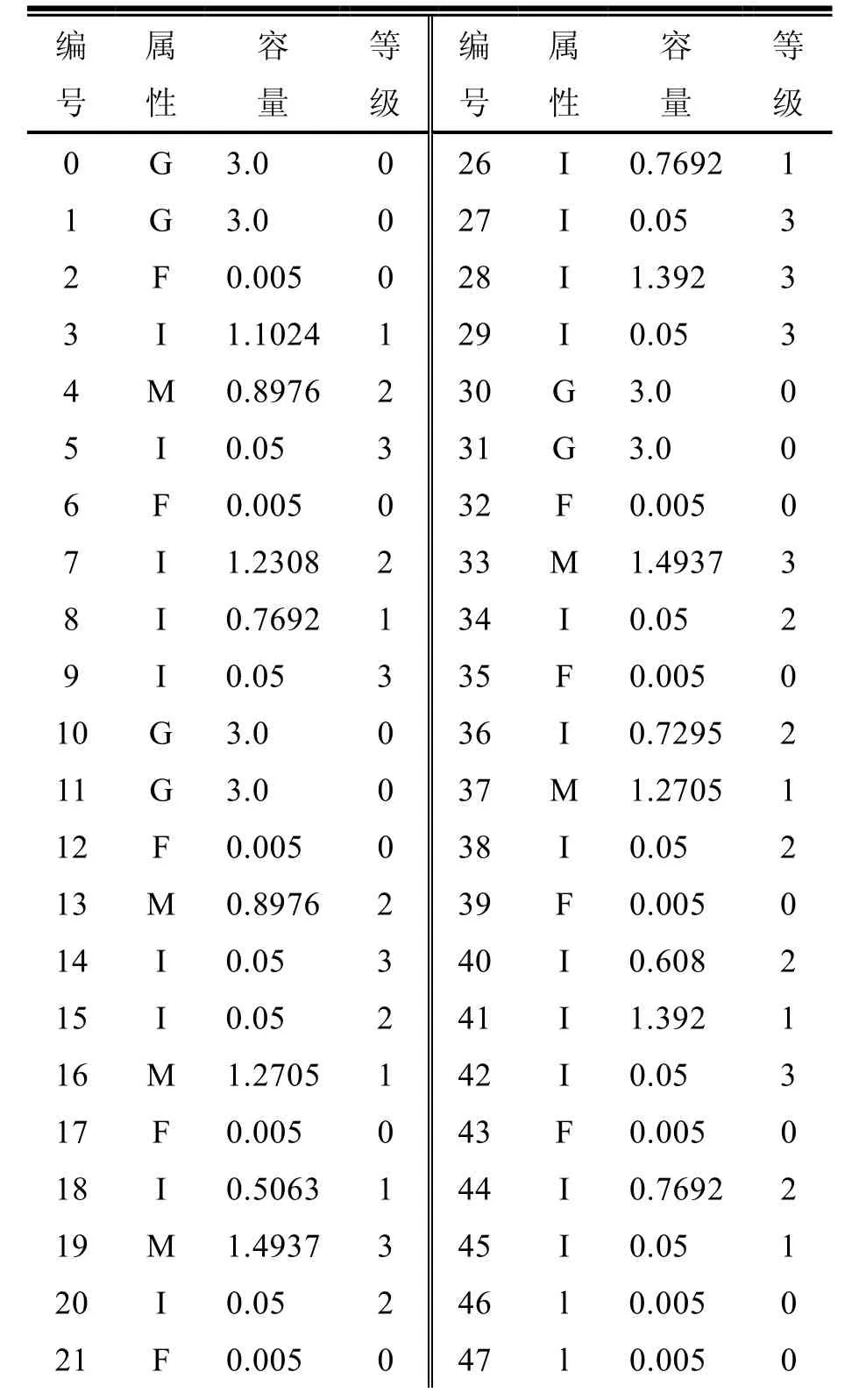
表1 船舶电力系统正常状态下设备参数

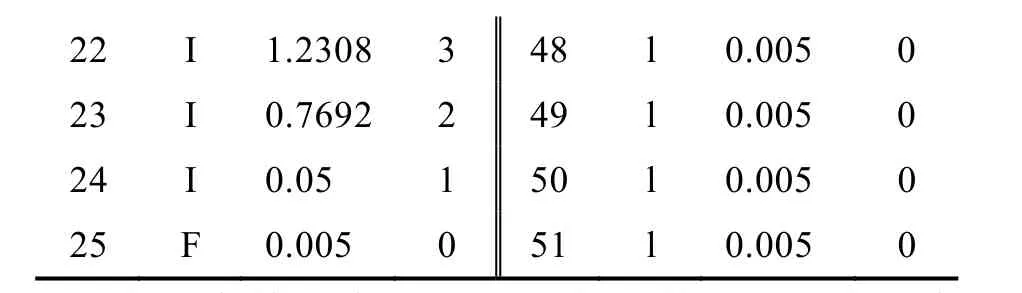
22 I 1.2308 3 48 l 0.005 0 23 I 0.7692 2 49 l 0.005 0 24 I 0.05 1 50 l 0.005 0 25 F 0.005 0 51 l 0.005 0

在仿真算例中，设定迭代次数为100代，初始化后，系统正常运行情况下的个体编码为：

111111111111100001111111110000111001111 111110011111。

算例1：假设具有备用路径的馈线单元9发生故障。

故障后的个体编码：

111111111011100001111111110000111001111 111110011111.

经过粒子运算得到最终结果为：馈线 Agent粒子单元27处：初始值为0，终极值为1。

对应的适应度为5.63265，开关次数为1。

其每一代最佳个体的适应度和开关变化次数过程如图4所示。

从图中可以看出，馈线Agent粒子单元9在发生故障的情况下发挥其自治特性，与邻近馈线Agent粒子单元联系，选择备用路径（馈线Agent粒子单元27）进行交互供电。另外，虽然在第16代时适应度值已经达到最优值，但是基于目标函数中关于开关次数最少的要求，Agent粒子单元会继续运算，在第19代时适应度值最优，开关次数仅为1次，满足系统要求。

算例2：假设故障为馈线Agent粒子单元11、20、21、24、49等五处，各有0级、1级和2级负载故障，即电站4失电，节点7断路。故障后的个体编码为

111111111110100001110011010000111001111 111110011101

经过粒子运算仿真得出：

Agent粒子单元7向Agent粒子单元4请求协助；

馈线 Agent粒子单元 34处： 初始值为：0，终极值为：1

馈线 Agent粒子单元 44处： 初始值为：0，终极值为：1

馈线 Agent粒子单元 45处： 初始值为：0，终极值为：1

对应的适应度：5.61035 开关切换次数：3

其每一代最佳个体的适应度和开关变化次数过程如图5所示。当迭代次数为28代时，可以得到全局最优解。

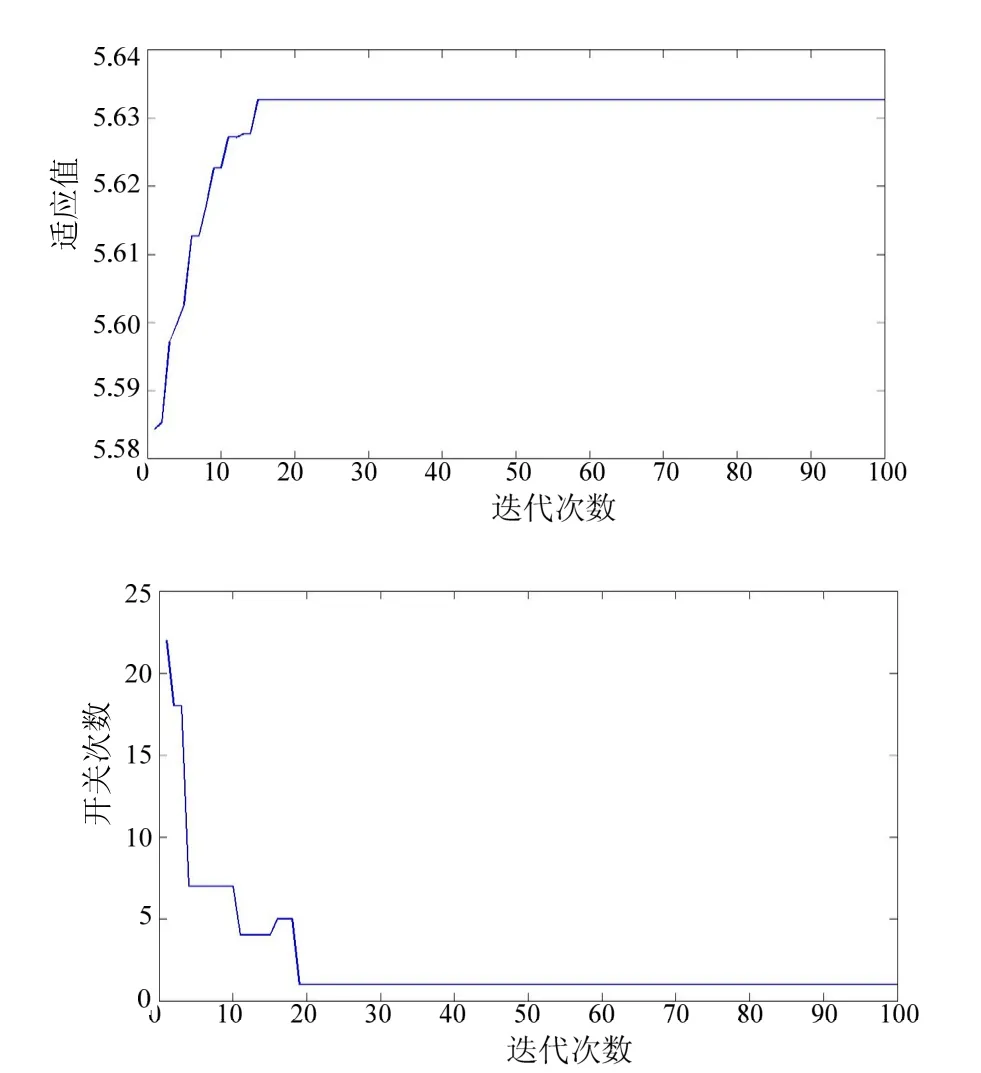
图4 算例1适应度和开关切换次数进化过程

从仿真结果可以看出：节点 7断电，节点Agent粒子单元 7向上级馈线 Agent粒子单元请求协助，节点4和10根据自身的馈线Agent粒子单元自身裕度回应节点Agent粒子单元7的协助请求。在满足潮流计算平衡方程和约束条件时，节点4回应请求，可以实现最大限度供电。同时，在馈线Agent粒子单元自治情况下，优先考虑临近馈线Agent粒子单元的协助动作，如馈线Agent粒子单元44处和45处，尽管节点4与7有协商合作动作，但是这不改变I11和I12从馈线Agent粒子单元44处和45处取电。

在上述算例的基础上，与传统的普通粒子群算法加以比较。针对上述算例1和算例2分析，统计结果如表2和表3所示。

综合仿真统计结果，可以得到：多Agent在船舶电力系统中的应用极大的提高了智能重构效果，加快了全局收敛和寻优能力。算例1中，在计算结果相同的情况下，粒子群算法的进化特性加快了寻优速度和收敛效果。算例2中，普通粒子群算法中以卸载负载转移供电为途径进行全局寻优，而本文算法发挥其馈线Agent粒子单元自治性和能动性的特性，主动向临近节点Agent粒子单元发送请求协助，最小范围内改变网络拓扑结构，平衡潮流计算，实现智能选择控制。

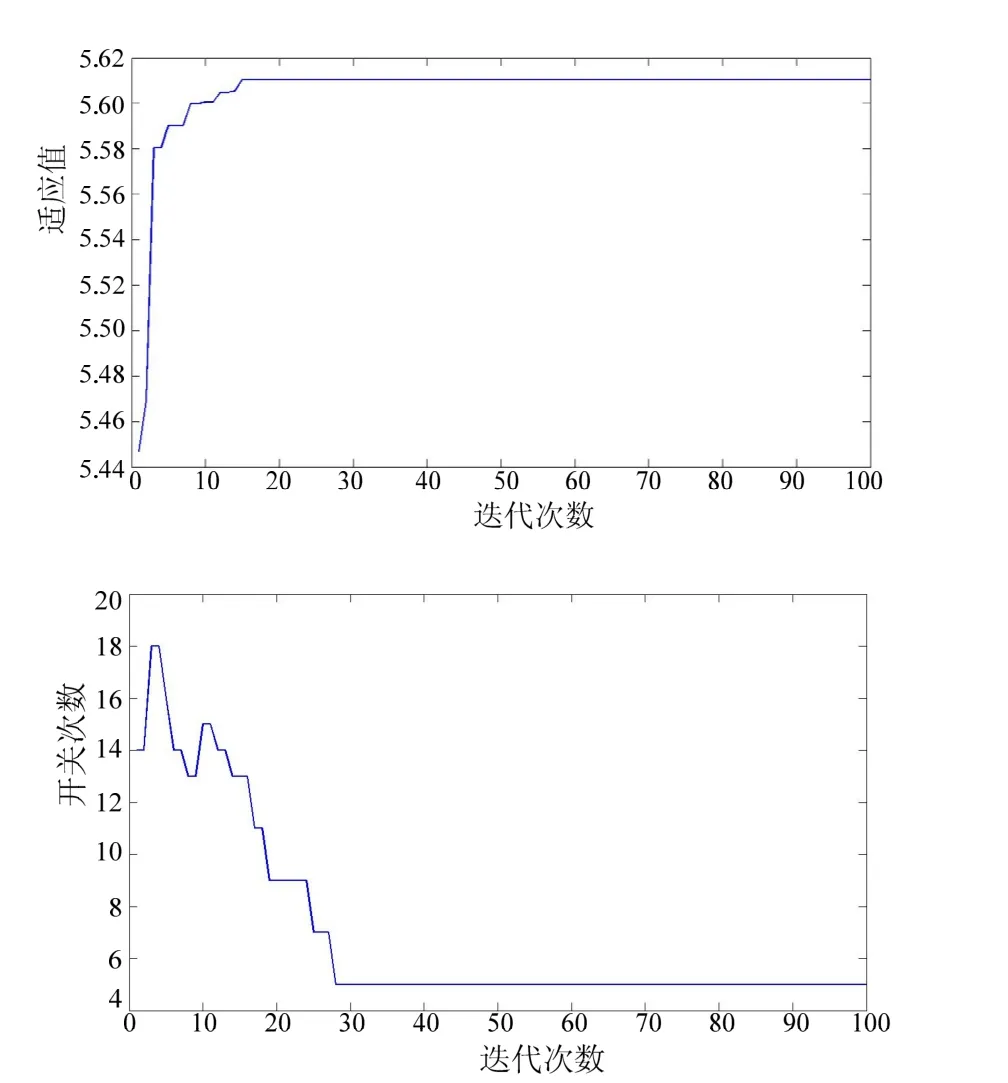
图5 算例2适应度和开关切换次数进化过程

4 结束语

从船舶电力系统网络拓扑入手，化简其为带有节点-支路的环状结构图，然后确定了其数学模型，确立了最大恢复供电和最少开关切换次数的数学目标，继而根据区域馈线的概念定义了节点支路为馈线Agent单元的软件实体。结合粒子群算法的粒子特性，将每个馈线Agent单元定义为一个粒子。通过对粒子群算法的改进，使得其进化特性在算法中得到充分体现，这样与多 Agent共同加大了系统适应度的寻优能力，较快的结束循环收敛。最后，与普通的粒子群算法在两种算例的分析比较，证实了基于多Agent粒子群算法在船舶电力系统网络重构应用中能够取得较好的全局寻优能力和计算效率。

表2 两种遗传算法针对算例1的统计结果

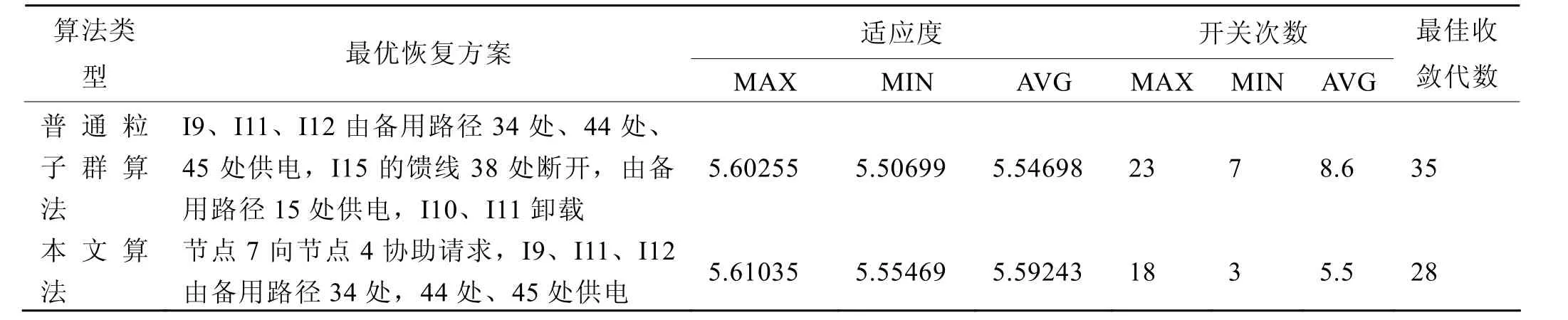
表3 两种遗传算法针对算例2的统计结果

[1]王征, 王永骥, 李哲. 基于改进蚁群算法的船舶电力系统故障重构研究[J]. 计算技术与自动化,2010,29(1)： 1～4.

[2]王征, 王家林, 姚刚等. 基于多 Agent的船舶电力系统故障诊断系统设计[J]. 船电技术, 2010, 30(5)： 1～6.

[3]杨秀霞, 张晓锋, 张毅等. 基于启发式遗传算法的舰船网络重构研究[J]. 中国电机工程学报, 2003,23(10)： 42～46.

[4]肖鲲, 黄挚雄. 多智能体粒子群算法在配电网络重构中的应用[J]. 计算机工程与应用, 2010, 46(8)： 221-224.

[5]Morejon.G, Srivastava.S.K, Cartes.D.A. Integrating Virtual Test Bed and JADE Agent platform Using CORBA for Reconfiguration of Shipboard Power Systems. In： Power Engineering Society General Meeting of 2006, June ,2006：1～6.