锅炉汽包虚假水位软测量模型的建立与仿真
2011-07-03张进
张 进
(杭州杭联热电有限公司,杭州 310018)
0 引言
锅炉汽包水位调节的任务是:使锅炉的给水量适应蒸发量;维持锅炉水位在允许的范围内。对于任务一,我们只需关注锅炉的“真实水位”即可,但是为了达到任务二的要求,只关注“真实水位”是不够的。汽包水位会对锅炉运行的安全性和经济性产生重要影响,也是锅炉运行的重要参数。汽包水位控制的好坏直接影响到火电厂运行的安全、稳定与经济性。所以,长期以来,锅炉汽包水位的测量与控制都是火电厂仪控专业的最重要课题之一。
1 引起锅炉汽包虚假水位的因素分析
1.1 给水量扰动下水位变化的动态特性
给水量G的扰动是给水自动控制系统中影响汽包水位的主要扰动之一,因为它是来自控制侧的扰动,一般称之为内扰。基于物质平衡的角度,给水量G加大之后,水位应立即上升,但实际水位并不会立即发生变化,而是需要延迟一段时间,甚至会出现先下降后再上升的情况。这是由于给水温度比省煤器的温度要低得多造成的。给水被控对象内扰的特点是:给水扰动刚刚加入时,由于给水的过冷度影响,水位H的变化速度很慢,经过一段时间之后其变化速度才逐渐增加,最后变为按一定速度直线上升,这时就只是物质不平衡在起主要作用了,如果给水流量和蒸汽流量不能平衡,水位将不能稳定。水位在给水扰动下的传递函数可表示如下:
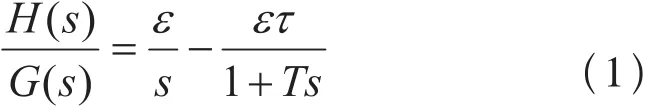
式中;ε为水位的飞升速度,τ为延时时间。
1.2 蒸汽流量扰动下水位变化的动态特性
“虚假水位”现象是由于负荷增加时水面下汽泡的容积增加得很快。待汽泡的容积已与负荷相适应并且达到稳定状态后,水位就会随物质不平衡关系的变化而下降。虚假水位变化的幅度与锅炉的汽压和蒸发量变化的大小有关。如果考虑到物质平衡,蒸发量骤然增加至ΔD时,蒸发量便会高于给水量,由于汽包水位没有自平衡能力,那么水位将直线下降,但是,实际水位依然先上升再下降,出现“虚假水位”的现象。其原因是负荷的增加使得蒸发强度在汽水循环回路中的也将成相应成比例的增加,此时水面下汽泡的容积增加得也很快,而燃烧量M还未来得及增加,汽包中汽压Pb下降,汽泡膨胀,使汽泡体积增大而水位上升,过了一定时间后,当汽包容积和负荷相适应而达到稳定后,水位就要反映出随物质不平衡关系而下降。因此,测量水位的变化应是上述两者之和,即:

蒸汽流量扰动时,水位变化的动态特性的传递函数也为两者的代数和:
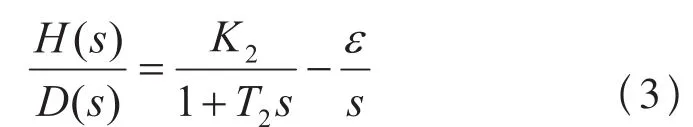
式中:ε为反映物质平衡关系的水位飞升速度,T2表示曲线H2(t)的时间常数,K2表示曲线H2(t)的增益。
2 用BP神经网络实现对虚假水位的建模
2.1 辅助变量的选取
由于给水流量、蒸汽流量对虚假水位的影响是一个动态过程,因而,如果某时刻给水流量或蒸汽流量发生变化,则虚假水位不仅仅影响当前时刻的虚假水位,而对之后一段时间内的虚假水位都有影响,因此,输出量应为能体现虚假水位动态变化过程的向量,记为下式:
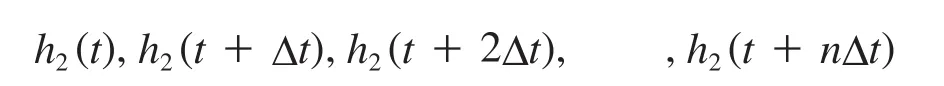
其中n的大小由输入变量对虚假水位的影响过程及时间间隔Δt决定。下面我们来观察给水流量和蒸汽流量对虚假水位的影响过程。
2.2 模型参数设计
将原测量仪表所测得的汽包水位减去真实水位(第三章所得模型仿真所得)看作理想的虚假水位,利用121次不同工况的实验数据中的60组作为学习参数,另外60组数据作为模型验证参数。
3 用RBF神经网络实现对虚假水位的建模
3.1 RBF神经网络原理
Powell.M.J.D于1985年提出了多变量插值的径向基函数,Broomhead.D.S和Lowe在1988年首次将RBF应用于人工神经网络设计,构造了径向基人工神经元网络,即RBF神经网络。从此人们展开了RBF神经网络的一系列研究,也取得了不少可喜的成果。已有定理己经证明了RBF网络完全可以对非线性函数进行逼近及逼近的唯一性。RBF网络不但具备BP网络所具有的强大的非线性映射特性、容错性、自适应性、并行处理及信息综合处理能力等一般网络特性,还具有比BP网络更强的局部逼近能力,不容易陷入局部极小点,训练速度快等特点。
RBF网络是一种有导师的三层前馈网络,结构与BP网络类似,第一层为输入层,由信号源节点组成,第二层为隐含层,单元数视精度要求而在给定的范围内自动选定,第三层为输出层,它对输入模式的作用作出响应。网络一般可以用下式来描述:
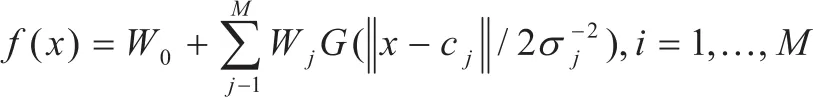
G=(||x-cj ||/2σj-2),i=1, ,M称作基函数,它属于RBF函数,一种局部分布、对中心点径向对成衰减的非负非线性函数,最常用的基函数G ( .)是高斯核函数。其表达式描述如下:
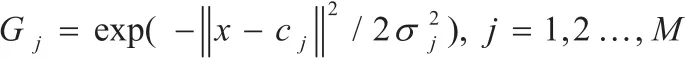
其中Gj是隐层第j个单元的输出,σj是第j个隐节点函数的归一化参数(或称宽待参数),它决定该中心点对应基函数的作用范围。其中X=(x1, x2, , xn)T是输入层的输入矢量,cj为第j个单元基隐层函数聚类中心向量(每个隐层中心的中心向量存储在其与输入各种神经元之间的连接中心),一般通过各种聚类方法得到。而|| .||表示N维空间中矢量之间的距离(通常为欧氏空间)。
网络每个输入层节点的输出为其与各隐层神经元输出Gj的加权求和。按高斯分布函数的定义,隐层神经元的输出 ,与输入矢量X的函数关系应服从正态分布,即当X与中心矢量cj的距离很近时,Gj接近最大值;反之Gj减小。如X与cj的距离超过宽度σj(即远离中心时),输出Gj可近似为零,相当于对输出层没有贡献。这就实现了局部感知,使得RBF网络比BP网络具有更强的局部逼近能力。
BP网络因借助网络层次之间广泛的非线性组合,故其外部的输入输出关系取决于所有神经元及其相互间连接权值。然而在RBF网络中,情况有所不同,以高斯网络为例,网络的总体输出由M个脉冲函数项线性组合而成。它的来历是基于大脑皮层中存在着局部、重叠的感受域这一特性提出的。如果网络基函数的宽带参数很小,则网络有十分精确的映射能力,映射误差可为零。但只要输入模型中稍带噪声,映射误差便骤增。为了避免这一现象出现,则应减缓高斯函数向两侧的衰减速度,即要增加高斯函数的宽度,并使各曲线之间有一定程度的重叠,以实现平稳的过渡。
3.2 用RBF神经网络实现虚假水位软测量建模及仿真分析
将原测量仪表所测得的汽包水位减去真实水位(第三章所得模型仿真所得)看作理想的虚假水位,利用121次不同工况的实验数据中的60组作为学习参数,另外61组数据作为模型验证参数。经过多次仿真试探,最终选取扩散系数为0.47737。
RBF神经网络结构为2-x-31,隐含层神经元数目x是在网络训练过程中,依据误差指标由软件自动确定的,本课题中训练得到x=55。所以得出RBF神经网络结构为2-55 -31。输出向量维数为31,能对工况变化之后310s内的虚假水位进行预测。
4 结论
本文采用的改进BP算法是共轭梯度法,网络结构为2-25-31,经过1000步训练后,网络的输出平均绝对误差为0.0024mm,当给水扰动为2t/h,蒸汽扰动为16t/h时,预测虚假水位最大绝对误差为1.05mm,当给水扰动为20t/h,蒸汽扰动为18t/h时,预测虚假水位最大绝对误差为0.3mm。
采用RBF神经网络时,经过50步训练,产生的网络结构为2-55-31,预测平均绝对误差达到3.3023×10-6mm,当给水扰动为2t/h,蒸汽扰动为16t/h时,预测虚假水位最大绝对误差为-2.7× 10-3mm,当给水扰动为20t/h,蒸汽扰动为18t/h时,预测虚假水位最大绝对误差为7.6×10-3mm。
可见,采用RBF神经网络比改进BP算法训练速度快得多,而且预测精度更高。这是选用RBF神经网络建立虚假水位预测模型的原因所在。
[1] 王学祥. 汽包水位监测系统的改进[J]. 江西电力, 2006,30(1): 18-20.
[2] 刘铭刚, 李国光, 周健.提高锅炉汽包水位测量准确度的研究[J]. 河北电力技术, 1999, (6): 13-16.
[3] 李文忠, 贾俊青, 阎有运. 锅炉汽包水位监视与报警器的研究[J]. 焦作工学院学报, 1998, (17): 213-216.
[4] 沈晓群, 杨震力, 邵军伟. 智能差压式汽包水位测量仪的设计[J]. 浙江海洋学院学报 (自然科学版), 2001, (04):306-310.
