基于MATLAB的水电工程项目工期仿真分析
2011-06-30吴正安
吴正安
(中国葛洲坝集团国际工程有限公司 北京 100022)
1 问题的提出
工程项目的进度受许多因素影响,项目管理者需事先对影响进度的各种因素进行调查,预测他们对进度可能产生的影响,编制可行的进度计划,指导工程项目按计划实施[1]。
根据关键路径理论,项目工期由关键路径上的一系列活动所决定,如果希望项目如期完成,则应密切关注关键路径上的任务和为其分配的资源。同时,在项目进行的过程中,关键路径会由一系列任务变为另一系列任务。因此,如何更准确地找到关键路径,确定最主要的关键路径,并由此计算项目工期的期望和方差等特征值,就成了项目管理者非常重要的事情。
本文对某水电工程项目工期进行了分析,利用科学的理论方法和计算机软件,估算出了在各种因素影响下各项活动持续的时间,继而确定了整个项目的关键路径,统计项目的主要关键路径,并计算得出了主要关键路径决定的项目工期的期望和方差等特征值。此外,本文还进一步对项目关键路径上的所有活动进行了仿真,分析关键路径上各活动按时完工的概率和各个活动对整个工程项目工期的影响程度。
2 项目概况及分析
2.1 项目概况
该水电项目位于缅甸境内,属于某流域水电资源梯级开发的电源电站项目。大坝为混凝土重力坝,主要由左岸非溢流坝段、溢流坝段、泄洪排沙孔坝段、右岸非溢流坝段组成。整个项目包含导流工程、大坝土建工程、镇墩、支墩及引水隧洞工程、钻孔、灌浆、排水工程、安全监测、建筑装修工程、水土保持永久措施工程、永久交通工程、水力机械设备和管路系统、电气一次、电气二次、暖通空调主要设备、消防系统、金属结构制作及安装工程等。
2.2 影响该工程项目进度的因素分析
由于该工程属于大中型工程项目,施工周期较长,影响进度的因素纷繁复杂,如政治、经济、气候、资金、人力、物资供应、对内对外交通条件和场地条件等因素,这些影响因素使得工程项目进度计划在执行过程中表现为可变性和不均衡性。
根据以往工程建设经验和历年相关资料记载,结合项目的实际情况,并预测项目实施过程中可能出现的问题,对影响工程项目进度的因素进行了分析。工程进度的主要影响因素如下:
a.政治不稳。该地区属于缅甸地方军队割据范围,且项目实施期间正值缅甸全国大选,政局不稳,出现无法预料的突发政治性事件的可能性大。如果战事一旦发生,将对项目的实施造成致命影响。
b.气候条件不利。工程地处亚热带气候区,由前期考察得知,该地区一年中至少有4个月是降雨集中期,意味着将有4个月属于雨季施工,这不仅会降低工作效率,更会加大项目防洪度汛的难度;此外,长时间降雨也会破坏道路,影响对内对外交通。
c.工程变更可能性大。由于该工程位于缅甸的边远落后山区,水文地质资料缺乏,加上前期工期压力大,工程勘探设计深度不够,必将导致工程实施过程中存在诸多工程施工变更,大大影响工程施工进度。
d.材料、物资供应进度的影响。工程项目配套的材料、物资和机具均来自中国,因此材料物资供应计划的改变、供应的不及时或不满足合同中规定的质量、技术标准等都会影响工程项目的实施。
e.工程项目的组织不当。该工程在短时间内资源(包括劳动力、材料、机械设备、管理)投入大,相关方(缅方政府、地方军队、中缅海关、业主、监理、设计、供货单位等)多,工程管理协调难度大,容易出现死角。
3 工程施工组织进度计划
3.1 主要分部分项施工工序
按照相关的理论对整个施工项目进行分解,主要包含两大块施工内容:
a.导流工程。导流洞开挖→洞身支护→洞身衬砌→洞身回填灌浆及固结灌浆→导流洞进出口岩坎拆除→钢筋石笼拦沙坎→大坝围堰填筑、拆除→导流洞下闸、混凝土封堵。
b.大坝主体工程。大坝及引水洞、灌浆平洞开挖与支护→大坝及引水洞、灌浆平洞混凝土浇筑→引水洞、灌浆平洞回填灌浆及引水洞固结灌浆→大坝固结、帷幕灌浆,及排水系统施工→金结、机电、消防设备安装→建筑装修→工程竣工资料整理及竣工验收→工程竣工资料及实物移交。
3.2 施工进度计划及其不足
3.2.1 施工进度计划网络图
在项目施工进度网络图中,整个项目共包括85个节点、110多个活动,其中有76个实活动。为了方便研究,我们结合有关的理论在不改变工程项目关键路径的条件下对施工进度网络图进行了合理的简化,简化后的施工进度网络图如图1所示。
图1中,带数字的圆圈表示节点,箭线表示活动,箭线上的字母表示活动的名称,括号中的数字表示该项活动的持续时间均值,网络图的各对应节点及其持续时间见表1。
3.2.2 施工进度计划的不足
该施工进度计划中,虽然使用了网络计划这一进度计划的有效工具,但它还是和其他传统进度计划一样,存在着诸多不足。
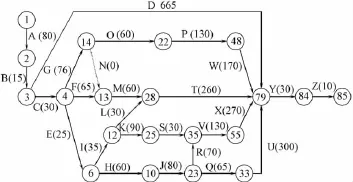
图1 施工进度网络图
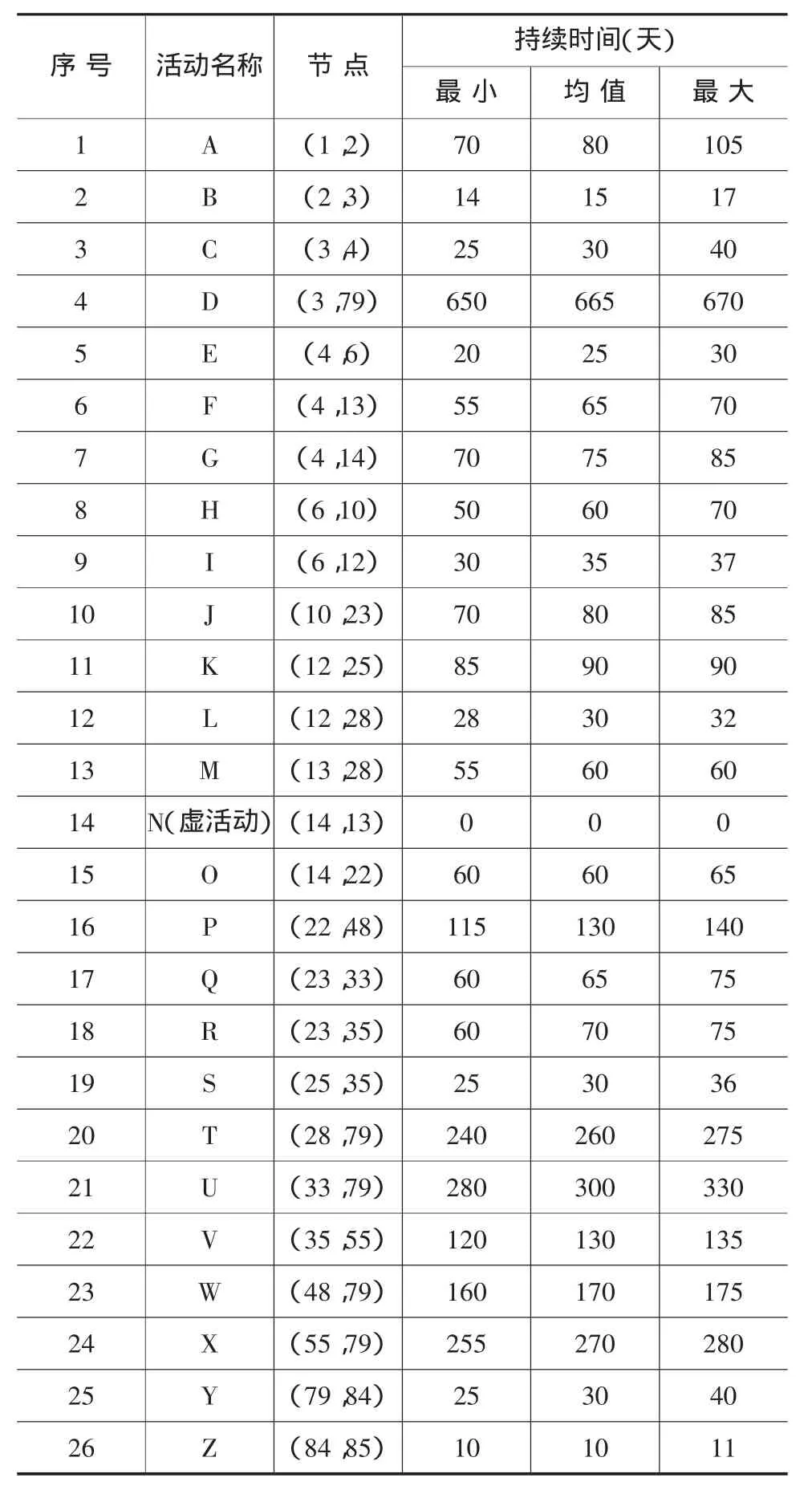
表1 活动持续时间
a.该网络图属于确定型的网络图,假定了各活动的时间是确定的。这与实际情况不符,因为由于受到诸多不确定因素的影响,各活动的持续时间通常都不会是一个确定的值,而是在某个范围内随机地波动。如果以一个确定值来衡量活动的持续时间,不仅不能很好地估计项目的活动时间,而且无法对项目活动持续时间的概率分布进行估计。这样做出来的进度计划往往会偏离实际进度计划较远,没有较强的活动时间变动的适应能力。
b.这种进度计划不能知道项目工期的期望和波动范围。由于传统进度计划假定项目活动持续时间是确定的,因此得到的项目工期也是确定的,这就无法知道项目工期的波动范围、概率分布及其按时间要求竣工的概率。
c.不能确定主要关键路径。在传统进度计划中,不知道在项目活动持续时间的不断变化过程中,哪些活动会成为关键路径,也不知道哪些关键路径最重要。
d.不知道关键路径上各活动的重要情况。因为假定各活动的持续时间是确定的,因此不知道哪些活动更加重要、更加关键,这样就会导致在项目管理过程中眉毛胡子一把抓。
e.不能对项目进度计划进行量化分析。不能对项目工期的波动范围、概率分布、竣工概率等进行量化分析;不能量化各关键路径的重要程度和各活动的重要程度。
各种影响因素存在于工程项目的各个活动之中,作用于整个项目的实施过程,由于这些因素对项目工期的影响,而使得传统的项目工期控制方法无法进行,从而需要采用新的理论方法MC(Monte Carlo)仿真方法对其分析控制。本文就是为了改进这些不足,用基于MATLAB的蒙特卡罗模拟技术来对项目工期进行模拟分析。
4 基于MATLAB的项目工期仿真分析
4.1 活动持续时间的确定
项目的活动时间是一个随机变量,它会受各种因素影响,因此具有高度的不确定性。即使经验丰富的项目管理专家事先也无法确知项目进行所需要的时间,而只能作近似的估计。在此,我们利用网络计划评审技术(PERT)对项目活动持续时间的计算方法,计算得出项目各主要活动的持续时间,作为我们仿真分析的数据基础。
由计划评审技术(PERT)方法计算每个活动期望mi的公式为

式中ai——第i项活动的乐观时间;
Ci——第i项活动的最可能时间;
bi——第i项活动的悲观时间。
计算方差的公式为

计算得到的项目活动持续时间的期望及标准差见表2。
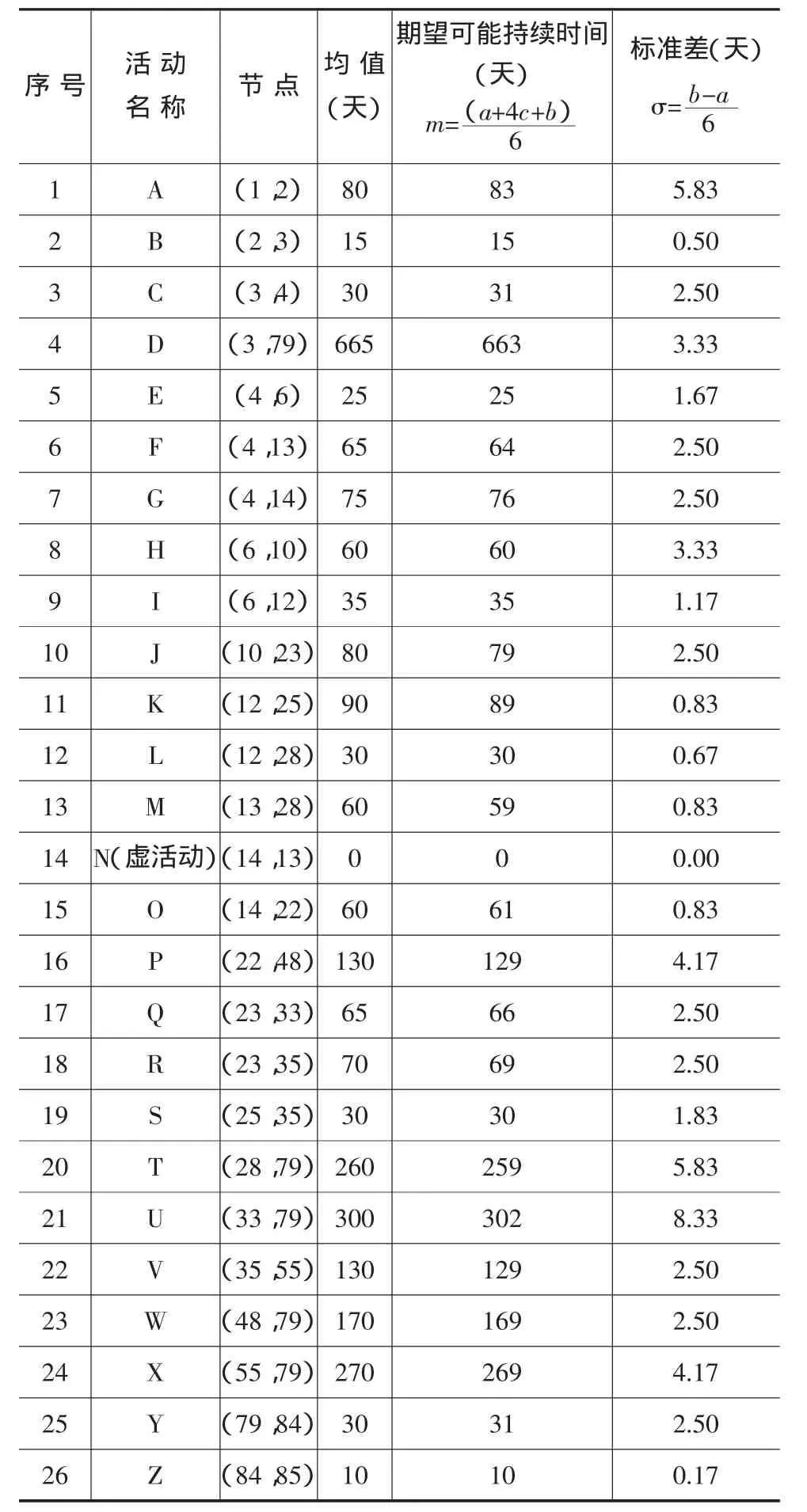
表2 活动持续时间期望及标准差
根据网络计划评审技术(PERT)计算得出的活动持续时间及其方差,对原网络图进行调整,得到的新网络图如图2所示。
图2中,带数字的圆圈表示节点,箭线表示活动,箭线上的字母表示活动的名称,括号中的数字表示该项活动的期望可能持续时间。
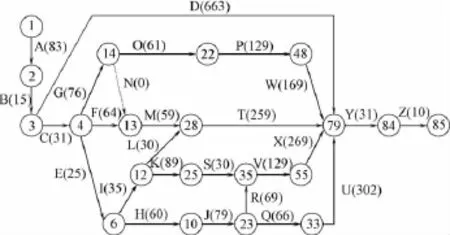
图2 调整后的网络图
为了实现对该项目工期的仿真分析,本文利用MATLAB的程序语言,使用了关键路径(CPM)原理、网络计划评审技术(PERT)、关键度指数理论等理论方法,编制了项目工期仿真软件,对项目工期进行了仿真。
4.2 仿真实现
利用计算机的蒙特卡罗模拟技术,能够产生特定概率分布的项目工期随机变量若干个,这能减少小概率事件对项目工期的干扰,较好地估计出项目工期的期望和方差。这就要求模拟的次数要足够多,在本文里,仿真次数设定为10000次。将上述计算得出的参数输入到仿真程序中,经过用MATLAB程序语言编写的仿真软件进行仿真和检测后得到了如下结果:
a.项目工期仿真样本的特征值。得到工期仿真样本的特征值如下:最小值(min)778.4717天;最大值(max)836.1625天;期望值(mean)804.7599天;中间值(median)804.5412天;标准差(std)7.8076。
b.项目工期概率图(见图3)及其在某时间限制下完工的概率(见图3)。项目工期概率图显示了仿真工期在各时间内的概率,能直观地看到确定工期下完工的概率;而“在815天内完工概率”为假定项目工期要求为815天,则项目能按时完工的概率为90.774%。
c.网络图关键路径及其出现概率。经过10000次的仿真得到的关键路径有两条,它们分别是:关键路径 1:1→2→3→79→84→85。其包含的活动有:A B D Y Z。
成为关键路径的概率:在10000次的仿真中出现了5472次,其概率为54.72%。
关键路径 2:1→2→3→4→6→10→23→35→55→79→84→85。
其包含的活动有:A B C E H J R V X Y Z。
成为关键路径的概率:在10000次的仿真中出现了4528次,其概率为45.28%。
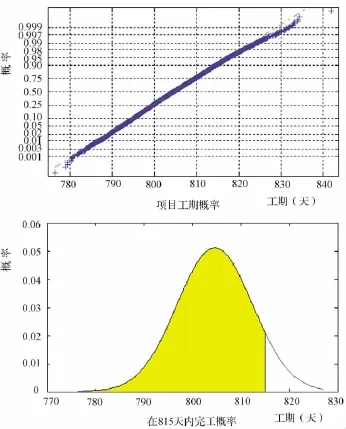
图3 项目工期概率图
d.关键路线上全部活动按时完工概率仿真。根据关键路径仿真结果得知,关键路径只有可能是两条,即1→2→3→79→84→85 和 1→2→3→4→6→10→23→35→55→79→84→85,包括的活动有A B C D E H J R V X Y Z,对这些关键活动分别进行仿真,算出各活动在一定时间内完工的概率,这里以各活动的期望加上标准差的时间内完工的概率,每项活动各取3个值的平均值,这样得到关键活动完工概率表(见表3)。
4.3 仿真结果分析
下面对仿真所得的结果进行分析:
a.根据工期概率直方图我们得到:最小值为778.4717天;最大值为836.1625天;期望值为804.7599天;中间值为804.5412天;标准差为7.8076天。即通过仿真后,整个项目的工期是以804.7599天为期望值、7.8076天为标准差的变量。根据正态分布规律,项目在±σ范围内即在797~813天完成的概率为68%;在±2σ范围内即在789~820天完成的概率为95%;而在±3σ范围内即在781~828天完成的概率为99%。因此,在没有重大不确定性因素的干扰下,整个项目最迟完工时间为836天,最早完工时间为778天,而最可能的完工时间落在781~828天的期间内。
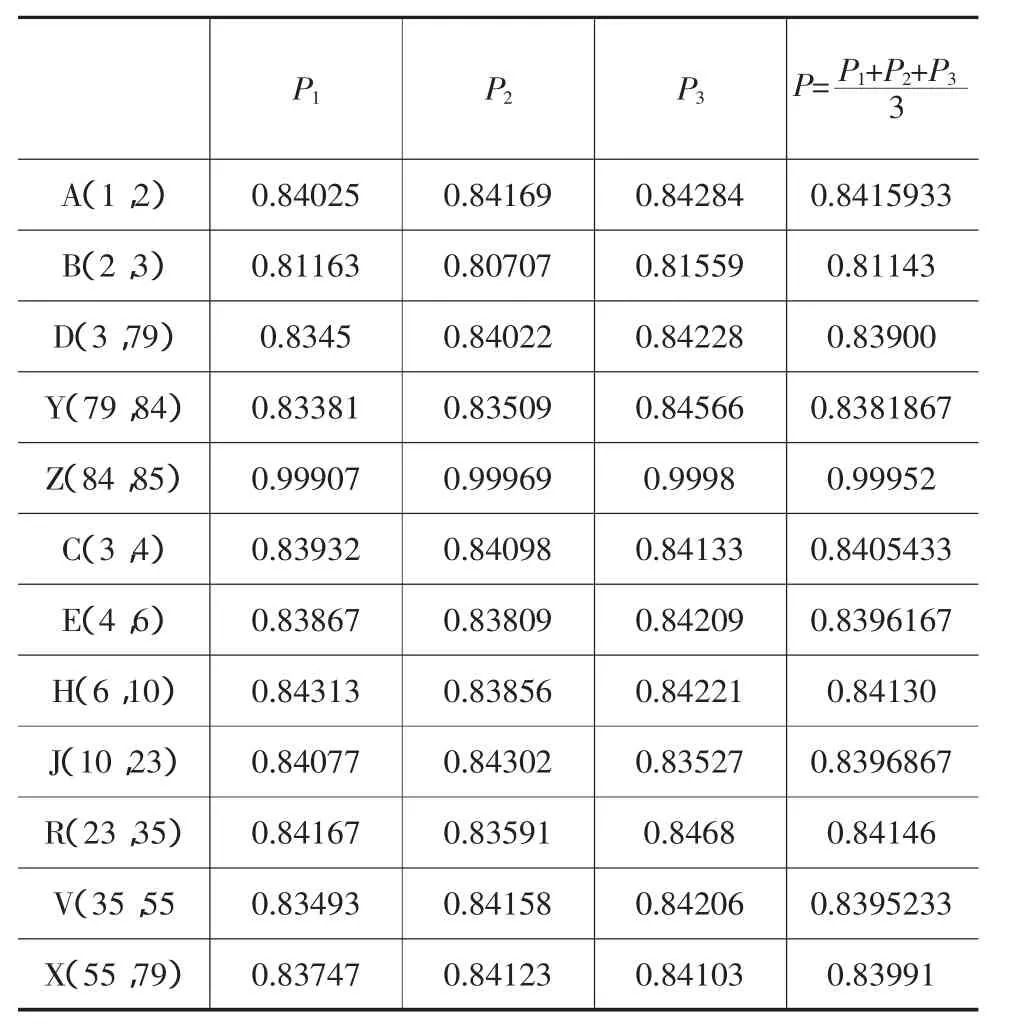
表3 关键活动完工概率
b.通过项目工期概率图,我们可以直观地看到项目工期小于确定天数的概率。从图4的上图中我们可以看出项目在830天内完工的概率为99.7%,即可以很有把握地说,项目能在830天之内顺利竣工验收;而项目在785天内完工的概率为0.3%,即在此时间内完工的概率非常小,可以认为是小概率事件,是不可能的事情。这就告诉我们如果要求在785天内完成,则其完成的概率几乎为0,也就是说,项目有不可压缩的最小周期,这是客观规律,是不能按主观意愿随意改变的,因此,项目管理者应该清楚,不能盲目地压缩工期,盲目地赶工,否则,不仅不能实现压缩工期的目的,而且会带来诸如工程成本增加和工程质量得不到保证的后果。在仿真中,我们假定项目工期的工期要求为815天,由图4的下图我们可以直观地看出,项目在815天内竣工验收的概率为90.774%。
c.在不确定型网络图中,由于各活动时间的变动,网络图中的关键路径很有可能会随之改变,或者在活动时间确定的情况下也有可能会出现多条关键路径。为了了解所有可能的关键路径出现的概率情况,我们在10000次的随机仿真过程中,对出现的关键路径进行了次数统计。在统计结果中我们看到,在模拟过程中,只出现了两条关键路径,说明项目工期主要受到这两条关键路径上活动持续时间的影响。然而,这两条关键路径出现的次数是不一样的,关键路径A→B→D→Y→Z在10000次的仿真中出现了5472次,其概率为54.72%;关键路径 A→B→C→E→H→J→R→V→X→Y→Z在10000次的仿真中出现了4528次,其概率为45.28%。这说明路径A→B→D→Y→Z比路径A→B→C→E→H→J→R→V→X→Y→Z更有可能成为网络图的关键路径,因此,它是最主要的关键路径,应该对其更加重视。同时我们看到两条关键路径都包含着活动A、B、Y、Z,而主要关键路径A→B→D→Y→Z除了这四项活动外只多了活动D,这说明活动D具有十分的重要性。这和实际情况是相符合的,因为活动D持续时间最长,牵涉的活动非常多,其持续时间也容易变动,因此,应对活动D进行持续的重点控制。
d.通过关键路径的统计,我们得出了两条关键路径。工程项目的工期主要受到关键路径上活动持续时间的影响,关键路径的总工期决定了整个项目的工期,为此,项目管理者都应该对关键路径上的活动进行重点控制。在此,我们进一步对关键路径上的活动进行了仿真分析,通过计算其在一定时间内完工的概率大小来衡量关键路径上各活动的“危险”程度。通过关键路径上各活动的“危险”程度分析,确定活动的危险性大小,对危险性大的活动实行重点控制。通过仿真分析得出的结果见表4。
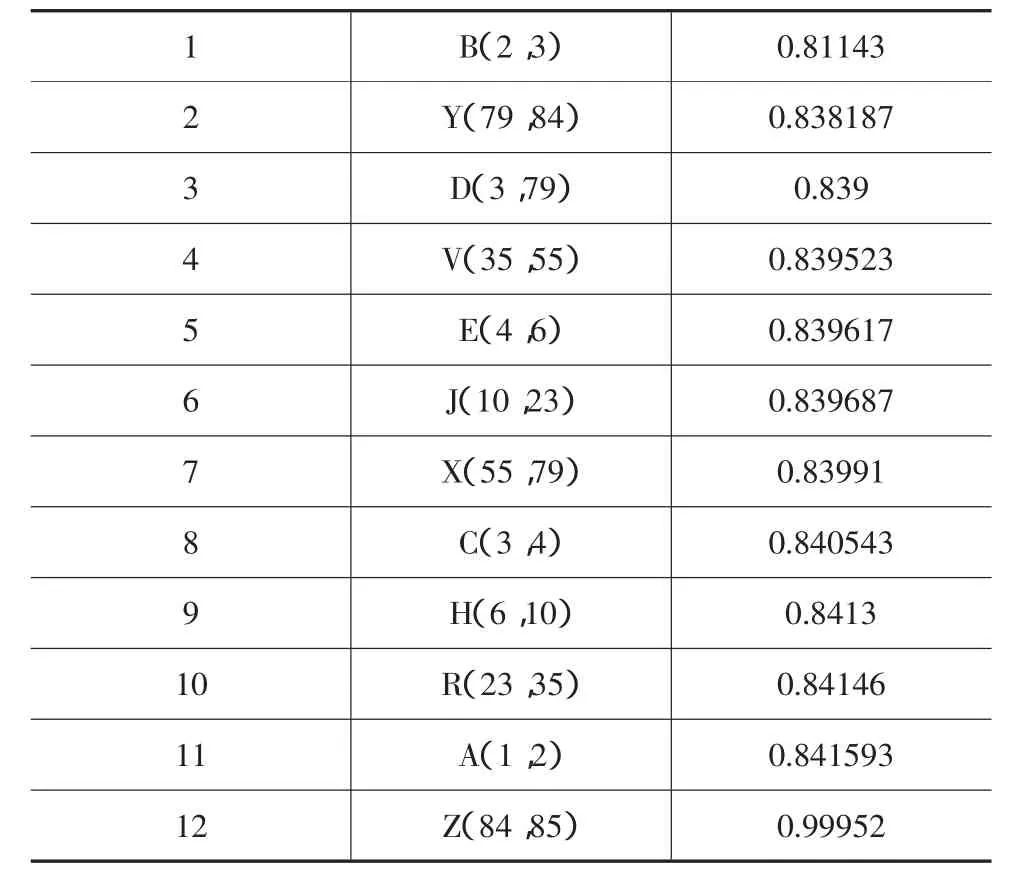
表4 关键路径上活动完工概率排序
由表4可知,延工概率最高的5项活动分别为B、Y、D、V、E,而在最主要关键路径上的活动为活动B、D和Y。因此,在按照延工危险程度高低进行重点关注和控制的同时,重点控制活动B、D和Y。
5 结论
通过对该工程项目进度的仿真分析,得到的结论可用图4表示。
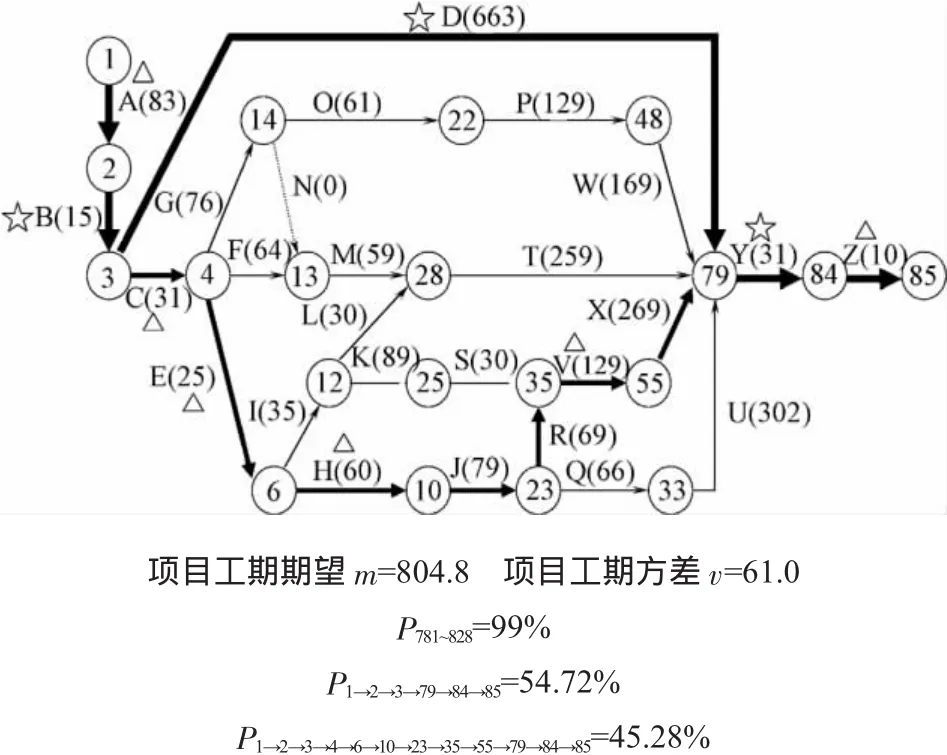
图4 结论图
图4中,标有五角星的活动为最重要、最关键的活动;标有三角形的活动为重要活动;箭头加粗的活动系列为关键路径;P781~828表示项目工期在781~828天内的概率;P1→2→3→79→84→85为关键路径 1→2→3→79→84→85 的概率,类似的,P1→2→3→4→6→10→23→35→55→79→84→85为关键 1→2→3→4→6→10→23→35→55→79→84→85 的概率。
下面对结论图作进一步的说明。通过基于MATLAB的蒙特卡罗仿真方法对该水电工程项目的工期进行仿真,得到如下结论:
a.项目工期期望和方差分别为804.8天和61.0天,项目工期以99%的概率落在781~828天,浮动天数为47天。
b.项目进度计划网络图中的关键路径有两条,分别为 1→2→3→79→84→85 和 1→2→3→4→6→10→23→35→55→79→84→85,它们的概率分别为 54.72%和45.28%,说明1→2→3→79→84→85为主要关键路径。
c.最重要的活动为活动B、D和Y,重要活动为活动A、C、E、H、V和 Z。
通过本文的分析和仿真的结果,能使管理者了解影响项目进度的主要原因,清楚项目工期的概率分布情况,了解项目进度计划网络图的关键路径及主要关键路径,并知道整个项目中最重要的活动及比较重要活动。这样,项目管理者可以了解到哪些活动对项目工期的影响更为显著,以便在项目实施中对这些活动给予更多的关注[2],抓住项目进度控制的重点,优化资源分配和进度控制,使项目安全有序地按时竣工验收并投入使用。
1石振武.建设项目管理[M].北京:科学出版社,2005.
2何正文,徐渝,朱少英等.GERT网络活动关键度指数的 Monte-Carlo 模拟分析[J].运筹与管理.2004(13).
3胡志根,黄建平.工程项目管理[M].武汉:武汉大学出版社,2004
4钟登华,刘奎建,杨晓刚等.施工进度计划柔性网络仿真的不确定性研究[M].天津大学,2005.
5王仁超,欧阳斌,褚春超等.工程网络计划蒙特卡洛仿真研究[M].天津大学建筑工程学院,2003.
