单桩承载力预测的PSO-Logistic模 型

吕锡岭

（浙江省大成建设集团有限公司，浙江 杭州 310012）

0 引言

近年来，随着国民经济建设快速发展，各地交通流量迅速增加，在沿海地区，许多高速公路的通行能力已不能满足经济发展的需求，急需对已有高速公路进行拓宽扩容[1]。自1997年以来，我国先后有广佛、沪杭甬、沪宁等多条高速公路进行了拓宽改造。由于沿海地区地质条件差，多为深厚软土地基，其强度低、压缩性大，易造成新老路基差异沉降大，给拓宽工程带来大量危害，因些，沿海地区拓宽工程的地基处理是拓宽成败的关键因素之一。

目前，拓宽工程中软土地基的处理方法有多种，其中预应力管桩以地基处理效果好、新老路基差异沉降小、施工快捷等优点得到了广泛应用[2]。确定管桩的极限承载力是拓宽工程中路基设计的重要内容，由于影响桩基承载力的因素众多，现有桩基理论还无法获得可靠的计算结果，一般需要进行试验研究。试验确定桩基极限承载力的方法有静载试桩法和动力试桩法，动力试桩存在一些很难避免的隐患，且人为因素影响较大，静荷载试验被认为是较准确、直观的方法[3-4]。静荷载试验是通过在桩顶分级施加轴向静载，记录桩顶荷载(Q)-位移(s)曲线，进而确定桩的极限承载力。但由于实践中很多被检测的桩本身就是工程桩，不能进行破坏性试验，所获得的是一条不完整的Q-s曲线，因此，根据已有信息对桩基的极限承载力进行预测是很有必要的，且目前已有多种预测方法。

本文参考自然界生物生长过程，分析静荷载作用下桩的Q-s曲线，将Logistic模型应用到单桩极限承载力的预测中，并在实例分析的基础上与常用预测模型进行了对比，验证了Logistic模型的合理性与预测精度。

1 单桩承载力的发展过程

在桩顶荷载作用下，桩的承载力包括桩侧阻力和桩端阻力2部分，如图1所示。在加载初期，荷载先由桩侧摩擦阻力支撑，随着荷载增加时，发生侧摩擦阻力的桩身长度逐渐增大，桩顶荷载基本上仍由桩侧摩擦阻力支撑，而桩端支撑的阻力较小。当桩侧摩擦阻力在整个桩身上全部发挥达到极限后，继续增大的荷载则由桩端阻力来承担。随着桩端持力层的压缩和塑性挤出，桩顶位移增长速率逐渐增大，直至桩端阻力达到极限，位移急剧增大而破坏，此时桩所承受的荷载即为桩的极限承载力。

在静荷载作用下，典型的桩顶Q-s曲线见图2。

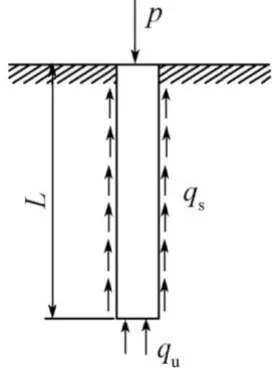
图1 桩的荷载传递Fig.1The load transfer of pile

图2 静荷载作用下桩的Q-s曲线Fig.2The Q-s curve of piles under static load

根据桩顶的Q-s曲线，可将桩的承载力变化分为3 个阶段[5]：

1）0～1段，承载力变化的弹性阶段，桩身各点的侧摩擦阻力都小于极限侧摩擦阻力。

2）1～2段，承载力变化的弹塑性阶段，当桩侧摩擦阻力达极限时（点1），桩侧土达到塑性状态，失去抗变形能力，随着桩顶荷载增大，塑性范围不断扩大，桩顶的抗变形刚度不断下降，Q-s呈非线性关系，直到桩长范围的桩侧土均达到塑性状态（点2）。

3）2～3段，新增加的荷载全部由桩端承担，直到持力层破坏，桩的承载力达最大值。

可见，静荷载作用下单桩的承载力变化是一个动态发展过程，经历了事物发生（开始加载）、发展（弹性、弹塑阶段）、成熟并趋于饱和（达到极限承载力）的过程，这一过程与生物的生长过程具有一定的相似性。

2 单桩承载力预测的Logistic模型

2.1 Logistic函数模型

Logistic函数模型为一条S形曲线，可以反映事物的生长发展过程，在生态学、人口学等领域得到了广泛应用，其具体函数形式为[6]：

式中：Y为yi的极限参数，即饱和值；

a为未知参数；

b为速度增长因子；

ti为不含误差的确定性时间变量。

Logistic曲线存在一个拐点，曲线过此点由下凹变成上凸，表明在拐点前曲线增长率逐渐变大，拐点后增长率逐渐变小，最后达到饱和状态。

Logistic是一种时间函数模型，但该时间是广义的，对于非时间物理量同样适用。将该模型用于桩基承载力研究时，可将式（1）表示为：

式中：si为桩顶位移，单位为mm；

S为最终沉降量，单位为mm；a和b为待求参数；

pi为荷载，单位为kN。

2.2 Logistic模型参数估计的PSO算法

当Logistic模型用于单桩极限承载力预测时，其关键是参数S, a, b的估计。目前，可用于参数估计的方法较多，如最小二乘法、神经网络法、支持向量机（support vector machine，SVM）、遗传算法等，文献[7]提出了参数估计时计算初始值的三段法。本文采用粒子群优化（particle swarm optimization，PSO）算法[8]进行参数估计。

PSO算法源于对鸟群捕食行为的研究，通过群体中个体之间的协作和信息共享寻求最优解。PSO算法是一种进化算法，一般从随机解出发，通过迭代寻找最优解，根据适应度评价解的品质，追随当前搜索的最优值寻找全局最优。PSO算法的进化方程为：

式中：i为粒子数，i=1, 2, …, m ；

k为迭代次数；

n为空间维数；

c1和c2为加速常数；

R1和R2为介于[0, 1]间的随机数；

gbesti为整体粒子群在历代搜索过程中最佳适应度值所对应的解；

pbesti为第i个粒子的个体最优解，即为第i个粒子最佳适应值所对应的解。

PSO算法在各类优化问题中得到了广泛的应用，并且许多计算软件中都提供其算法单元，可以直接调用。如1stopt不仅提供了粒子算法，而且采用全局优化法，计算时不用提供参数的初始值，可以自由设置迭代次数。

3 实例分析

3.1 工程概况

本文分析工程为上三高速SK1+260～SK4+494段，为上虞枢纽互通区被交路主线。由于上虞枢纽匝道接入上三线主线，该段需对主线进行拓宽为6车道或8车道。

地质勘察表明，该路段表层为耕植土，厚度为0.3～0.6 m，应清除，下部为淤泥质粉土，厚约7.4～28.2 m，分布不连续。软土层强度低，应进行地基处理，原上三线本路段采用了超载预压、塑板加超载预压、水泥搅拌桩的处理方式。自通车以来，已产生沉降7～20 cm不等，在桥台锥坡等处可见明显的沉降痕迹。为了提高地基承载力，使新老地基性质基本相同，避免或尽可能减小拓宽工程的差异，在SK1+260～SK1+340段两侧各80 m，采用管桩处理，管桩打穿软土层，桩径为400 mm，桩长为34 m。

3.2 单桩极限承载力静荷载试验

管桩施工结束后，按设计要求对SK1+260～SK1+340段抽选的3根管桩进行了极限承载力静荷载试验。图3为1#试验桩的荷载-位移（Q-s）曲线。在最大荷载550 kN作用下，桩顶沉降量为23.27 mm，荷载-位移曲线为缓变型。根据规范可确定该桩的极限承载力为550 kN，满足设计要求。

由于该桩为工程桩，不能进行破坏性试验，所以试验并没能获得完整的荷载－位移曲线，最大荷载作用下的位移也没有达到40 mm，这使得按最大荷载确定桩的极限承载力是很保守的，有必要对桩的极限承载力作进一步分析。

图31#管桩的Q-s曲线Fig.3The Q-s curve of Pile 1

3.3 基于PSO-Logistic模型的单桩承载力预测

按照上文提出的Logistic预测模型，在1stopt中编写计算代码，并调用PSO算法，将种群数设为20，c1和c2均设为2.05。经过3 000次迭代后获得模型的3个参数分别为 ：S=38.416 mm，a=72.406，b=0.008 5。各级荷载作用下的位移预测值见表1。

表1 1#管桩承载力的预测值Table1 The predicted value of bearing capacity for pile 1

从表1可看出，第1级荷载作用下预测值与实测值间差异较大，但随着荷载增大，预测值的精度越来越高，当荷载加载到550 kN时（第9级），预测值和实测值间的误差仅为-0.36%，预测值的精度较高。

3.4 与常用预测模型对比

由单桩静荷载试验获取的Q-S曲线分析桩的极限承载力，一直以来都是桩基研究的热点，研究人员先后提出了多种预测模型，如双曲线模型、指数模型、幂函数模型等。也有些学者将灰色理论（GM(1，1)）、人工神经网络（ANN）、支持向量机等方法应用到桩基承载力的预测中。

常用双曲线函数模型为

式中：Q为桩顶荷载，单位为kN；

s为桩顶位移，单位为mm；

K1为初始抗拔刚度，单位为kN/mm；

Qm为极限抗拔力渐进值，单位为kN。

指数函数模型为

图4为基于Logistic模型、双曲线模型和指数模型的预测值与实测值的Q-s曲线对比图。

图4 不同预测模式的Q-s曲线对比Fig.4Comparison of Q-s curves for different Prediction models

据图4可知，由双曲线模型和指数模型得到的预测 Q-s 曲线与实测曲线有明显差异，特别是随着荷载增大，差异越明显，用于桩的极限承载力预测时，其结果明显会偏小，而Logistic模型的预测曲线与实测曲线的吻合度较高，可见，Logistic模型更适合用于单桩极限承载力的预测。

3.5 其它工程的验证

文献[10]对2根型号分别为PHC-500(125)ABC80-10,10,11（81#）和PC-500(100)A-C60-9,7（105#）的工程桩进行了静载试验，试验结果见表2。为了分析PSO-Logistic模型应用于其它工程中的推广能力，进一步以表2中的数据进行分析，将PSO-Logistic模型的预测结果也列于表2中。分析可知，第1级荷载下的预测误差较大，但随着荷载增大，预测精度越来越高，第9级荷载下的误差仅为-1.37%和-1.36%。

图5为2根测试桩的预测曲线与实测曲线对比。从图中可见，2根桩的预测曲线都与实测曲线有较好的吻合度。

表2 预测值与实测值对比Table 2Comparison of predicted values and measured values

图5 预测曲线与实测曲线的对比Fig.5Comparison of predicted curves and measured curves

文献[11]对1根桩长为88.64 m，直径为1 100 mm的超长大直径钻孔灌注桩进行了静载试验，并建立了单桩的极限承载力预测GM(1,1)模型，其具有较高的预测精度（平均相对误差为1.54%）。为了对比，现调用本文建立的PSO-Logistic模型进行分析，将实测值、GM(1,1)模型预测值和本文方法的预测值绘制在同一坐标内，如图6所示。

图6 超长桩的实测与预测曲线Fig.6The predicted and measured curves of a super-long pile

由图6可知，GM(1,1)模型和PSO-Logistic模型的预测和实测曲线吻合都较好，可见，本文提出的PSO-Logistic模型具有较大的推广价值。

4 结论

1）桩的承载力变化规律是一个渐进的发展过程，同生物生长过程一样，经历了事物发生、发展、成熟并趋于饱和（极限）的过程。

2）静荷载作用下桩的荷载－沉降曲线可用Logistic模型描述。

3）Logistic模型的参数估计有多种方法，采用粒子群优化（PSO）算法可有效获得全局最优解。

4）实例分析表明，PSO-Logistic模型用于单桩承载力预测时，预测精度随荷载增大而提高。PSOLogistic模型比双曲线模型和指数模型更适合用于单桩极限承载力的预测，模型具有较大推广价值。

[1]李茂英，曾庆军，莫海鸿，等.高速公路拓宽工程沉降控制复合地基优化设计[J].岩土力学，2008，29(2)：535-540.Li Maoying，Zeng Qingjun，Mo Haihong，et al.Optimum Design of Composite Foundation According to Settlement Control for Extension Project of Expressway[J].Rock and Soil Mechanics，2008，29(2)：535-540.

[2]刘观仕，孔令伟，李雄威，等.高速公路软土路基拓宽粉喷桩处治方案分析与验证[J].岩石力学与工程学报，2008，27(2)：309-315.Liu Guanshi，Kong Lingwei，Li Xiongwei，et al.Analysis of Treatment Scheme for Soft Foundation in Expressway Widening Project and Its Verification[J].Chinese Journal of Rock Mechanics and Engineering，2008，27(2)：309-315.

[3]陈进光，冷伍明.粉喷桩单桩竖向抗压极限承载力预测方法[J].勘察科学技术，2004(4)：13-16.Chen Jinguang，Leng Wuming.Study on Prediction of Ultimate Bearing Capacity of Cement-Soil Mixed Pile[J].Site Investigation Science and Technology，2004(4)：13-16.

[4]王之军，刘建平，袁加贝.用函数模型外推法预测抗拔桩极限承载力[J].探矿工程：岩土钻掘工程，2005(9)：12-14.Wang Zhijun，Liu Jianping，Yuan Jiabei.Forecast of Extreme Limit of Anti-lifting Pile’s Bearing Capacity Function Model of Extrapolation[J].Exploration Engineering：Rock & Soil Drilling and Tunneling，2005(9)：12-14.

[5]李 亮，魏丽敏.基础工程[M].长沙：中南大学出版社，2005：217-222.Li Liang，Wei Liming.Foundation Engineering[M].Changsha：Central South University Press，2005：217-222.

[6]程毛林.逻辑斯蒂曲线的几个推广模型与应用[J].运筹与管理，2003，12(3)：85-88.Cheng Maolin.Several Promote Model of Logistic Curve and Its Application[J].Operations Research and Management Science，2003，12(3)：85-88.

[7]莫 云，岳 昊，胡 斌，等.基于Logistic预测模型的地铁隧道地表沉降预测研究[J].工程地球物理学报，2010，7(1)：115-119.Mo Yun，Yue Hao，Hu Bin，et al.A Study of Logistic Equation Applied to Predicting GroundSettlement Induced by Subway Tunneling Work[J].Chinese Journal of Engineering Geophysics，2010，7(1)：115-119.

[8]高 尚，杨静宇.群智能算法及其应用[M].北京：中国水利水电出版社，2006：3-5.Gao Shang，Yang Jingyu.Swarm Intelligence Algorithm and Its Application[M].Beijing：China Water Power Press，2006：3-5.

[9]李 森，唐孟雄.抗拔桩荷载－位移曲线拟合模型的比较分析[J].地下空间与工程学报，2009，5(4)：735-739.Li Sen,Tang Mengxiong.Contrast Analysis on Prediction Models for Load-Displacement Curve of Uplift Pile[J].Chinese Journal of Underground Space and Engineering，2009，5(4)：735-739.

[10]周晓杰.基于灰色预测理论的单桩极限承载力预测分析[J].芜湖职业技术学院学报，2010，l2(2)：31-34.Zhou Xiaojie.Prediction and Analysis on Ultimate Bearing Capacity of Single Pile Based on Gray Forecasting[J].Journal of Wuhu Vocational Institute of Technology，2010，l2(2)：31-34.

[11]张树传.灰色系统参数识别方法对桩承载力预测的影响[J].福建建筑，2010(11)：64-67.Zhang Shuchuan.Affection of Parameter Identification Method of Gray Theory in Predicting Overlength Pile Bearing Capacity[J].Fujian Architeeture & Construetion，2010(11)：64-67.