光纤布拉格光栅的分析及其剥层算法重构

刘丰年，李 娜，果 鑫，张文平，徐 勇，张 笛

（湖南工业大学 计算机与通信学院，湖南 株洲 412007）

0 引言

光纤布拉格光栅（fiber Bragg grating，FBG）是一种利用光敏光纤的光致折射率沿光纤轴向周期性变化的光纤波导。FBG独特的窄带滤波特性，及其易于同光纤系统集成的优势，使其成为目前最有发展前途、最具代表性和发展最为迅速的光纤元件，在光纤通信、光纤传感和光信息处理等领域得到了广泛应用[1]。在光纤光栅的研制中，想要达到理想的光纤光栅应用效果，需要对决定光纤光栅反射性能的调制参数进行计算，获取合适的参数才能得到理想的光纤光栅。因此，合适的参数设计对于制成拥有特定反射光谱的光纤光栅，具有重要的指导意义，对FBG基本原理及重构的分析和研究也更是广受关注。

为实现光纤光栅制作的理论指导，首先需掌握光栅光谱特性分析，在此基础上，还需研究实现光栅光谱重构的算法。因光谱分析较复杂且计算量庞大，目前基于耦合模理论的分段均匀传输矩阵法是较方便实用且常用的分析方法，其优势在于能对每小段光栅进行单独的参数设置，灵活性高，运算速度快，可快速计算具有105个周期的厘米级长度光纤光栅。光纤光栅重构即基于耦合模理论，通过某种算法计算出能够产生某种反射光谱及时延特性的光栅结构信息——耦合系数、反射率、折射率调制方式等。相对于根据光纤光栅的长度、周期、折射率调制方式来分析计算其反射谱而言，光纤光栅的重构又被称为光纤光栅的逆问题、耦合模逆问题[4]。

1 光纤Bragg光栅

从基本光学特性来看，FBG即是一个以其反射波长（亦称布拉格波长）为中心波长的窄带光学滤波器。其光学原理图如图1所示。

图1 光纤布拉格光栅的光学原理图Fig.1Schematic diagram of FBG based on optical theory

光纤光栅的布喇格波长λB取决于光纤纤芯的有效折射率neff和光栅周期Λ，即

FBG是利用光敏光纤的光致折射率变化，把光纤放置于紫外光形成的空间干涉场中曝光而在纤芯内形成的空间相位光栅。通常在光栅长度为L的小段光纤内写入周期为Λ的光栅前，纤芯芯区折射率为n1，写入后，芯区的折射率发生周期性的变化，下面给出有效折射率neff及其变化Δneff的关系，即

式中：Λ为光栅周期，即折射率周期；

当前众多的光栅写入技术，其光栅区域的折射率调制表示形式较复杂，但对通常采用相位掩模技术写入的FBG来说，其光致折射率的变化可简单表示为

式中ΔnDC和ΔnAC分别表示光栅折射率的直流调制幅度和交流调制幅度。

理想折射率调制情况下，条纹可见度V=l，即ΔnDC=ΔnAC。FBG属均匀光栅，其折射率分布如图2所示。从图中可见不变，=0，则FBG的折射率可写为

图2 FBG折射率分布图Fig.2The profile of FBG's refractive index

2 传输矩阵法分析FBG

运用分段均匀的传输矩阵法，将FBG分为无数个均匀光栅段，每个均匀光栅段由一个2×2矩阵进行描述，将无数个矩阵相乘，就得到描述完整光栅光谱特性的传输矩阵。对于均匀光栅，耦合模方程存在解析解，可给出其正反向光波通过光纤光栅前后光场间的关系，即

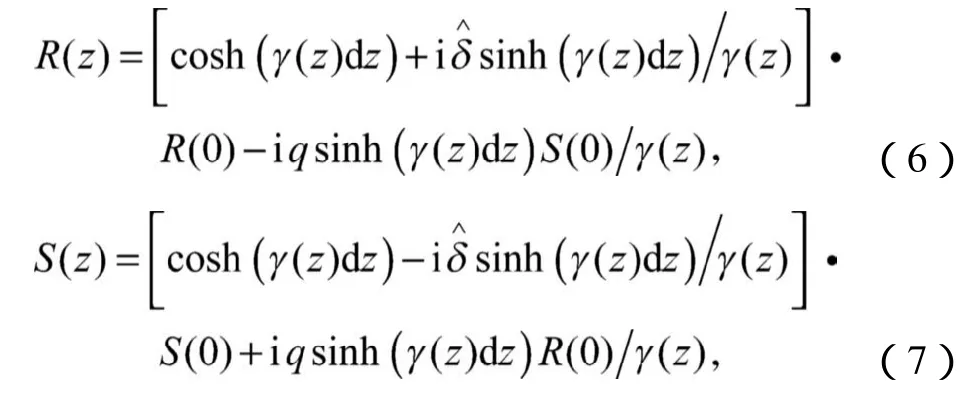
式中：R(z)为沿z轴正向传播的光波振幅；

S(z)为沿z轴反向传播的光波振幅；

q为耦合系数。

用矩阵形式描述正反向光波的光场为

式（8）等号右端的2×2矩阵即称为光栅传输矩阵。

采用均匀分段描述法，FBG可被分解为无数个均匀光栅段，每一段光栅的结束是另一段光栅的开始，利用式（8）对每一光栅段的正反向光场进行描述，若Fj（j=1, 2, …, ∞）表示任意一小段均匀光栅的传输矩阵[2]，即

那么，整个光栅的传输矩阵可用F表示为

对于整个折射率均匀的调制光栅，其入射波R和反射波S（见图3）之间的关系为[7]

式（11）中，对初始条件进行分析，由于在光纤光栅的起始端，前向传输波还没有与后向反射波发生耦合，所以必有

图3 光栅传输矩阵模型Fig.3Fiber grating transfer matrix model

3 剥层算法重构FBG

剥层（layer-peeling，LP）算法是一种基于因果规律的算法[6]。将长度为L的光栅分成足够多的N段，每一段长度为l，且周期均匀，同时，将每一段光栅看作一个反射系数为j(j=1, 2, …, N)的复反射器，耦合系数也被离散化为qj，光纤光栅就成为由多个复反射器级联而形成的因果系统，相当于上述传输矩阵分析法的离散分析系统，然后通过逐层递归计算光纤光栅的耦合系数，从而计算出光栅的折射率调制分布参数。

对反射率r进行归一化计算，可得其反射系数 。据剥层算法分析原理可知反射率的归一化振幅——反射系数可表示为，所以，光纤光栅的反射率可表示为

根据光栅耦合理论，反射系数与耦合系数的关系可表示为

同时，耦合系数与折射率调制的关系为

根据式（14）可计算耦合系数，由式（15）中q(z)的幅值即可求出光栅的折射率交流调制幅度ΔnAC(z)。

剥层算法重构FBG的具体实现步骤如下：根据因果系统的特性，光波在进入光栅前，第1层反射器的耦合系数q1仅由光波到达该层时的响应决定，从而获得第1段光栅的传输矩阵；据传输矩阵法，随着光波的传输，耦合效应传递到下一层，故当光波传输到第2层反射器时，只要基于因果效应剥离第1层反射器的耦合效应，就可以计算出第2层反射器的耦合系数q2；重复上述步骤逐层计算，就可得到每层反射器的耦合系数qj，然后，根据耦合系数qj的幅值求出光纤光栅折射率的调制规律，从而实现光纤光栅重构。

本文在理论研究的基础上，利用Matlab软件仿真一个目标带宽为1 nm、中心波长为1 550 nm的光栅反射光谱，仿真结果见图4。对比可知重构光栅的反射谱与目标反射谱的谱形基本一致，两者的反射率相差不到1.5%。

图4 光纤光栅的目标反射谱和重构反射谱Fig.4The reflection spectrum for the target and the reconstructed fiber Bragg grating

根据剥层算法计算得到目标FBG的耦合系数，图5所示为耦合系数的实数部分。利用耦合系数与折射率之间的关系，进而得到光栅的折射率调制幅度ΔnAC(z)的分布，如图6所示。由此可得Bragg光栅的折射率调制方式，同时计算了重构光栅反射谱的群时延，结果见图7。

图5 重构的光栅耦合系数Fig.5The coupling coefficient for reconstructed grating

图6 重构光栅的折射率调制分布Fig.6Refractive index modulation of reconstructed grating

图7 重构光栅的反射谱群延迟Fig.7The reflection spectrum of group delay for the reconstructed gratings

从图7中可看出：重构光栅的整个入射谱中最大的群延迟小于0.51 ps，相对于以往的计算结果[8]，其精度有了较大提高，且反射带宽区域内的群时延明显小于透射谱的群时延。根据剥层算法重构的FBG，反射出的光谱效果与目标光谱基本吻合，因此，剥层算法可以较好地指导能反射出目标光谱的FBG制作。

4 结语

本文从光纤光栅折射率调制原理入手，分析了FBG光栅的特性，利用传输矩阵法对FBG光谱进行分析，选择合适的切趾函数，对FBG重构原理进行了推导和详细阐述，并利用剥层算法实现了光栅的重构，达到了较理想的光栅反射要求。

[1]唐 利，彭拥军.光纤布拉格光栅非线性传输特性的数值研究[J].应用光学，2011, 32(2) ：308-316.Tang Li, Peng Yongjun.Numerical Simulation on Nonlinear Transmissive Characteristics of Fiber Bragg Grating[J].Journal of Applied Optics，2011, 32(2) ：308-316.

[2]Turan Erdogan.Fiber Grating Spectra[J].Journal of Lightwave Technology，1997(8) ：1277-1294.

[3]Feced Ricardo, Zervas Michalis N, Muriel Miguel A.An Efficient Inverse Scattering Algorithm for the Design of Nonuniform Fiber Bragg Grating[J].IEEE Journal of Quantum Electronics, 1999, 35(8)：1105-1115.

[4]黄 锐，周赢武，方祖捷.遗传算法及其在光纤光栅逆运算中的实现[J].光子学报，2002，31(增刊2)：79-86.Huang Rui, Zhou Yingwu, Fang Zujie.A Genetic Algorithm for the Synthesis of Fiber Bragg Grating[J].Acta Photonica Sinica, 2002，31(S2)：79-86.

[5]Belai O V, Frumin L L, Podivilov E V, et al.Finite Bragg Grating Synthesis by Numerical Solution of Hermitian Gel’fand-Levitan-Marchenko Equations[J].Optical Society of America, 2006(23)：2040-2045.

[6]Skaar Johannes, Wang Ligang, Erdogan Turan.On the Synthesis of Fiber Bragg Gratings by Layer Peeling[J].IEEE Journal of Quantum Electronics, 2001, 37(2)：165-173.

[7]刘长军，张伟刚，姜 萌，等.光纤布拉格光栅自致啁啾效应的研究[J].光学学报，2008, 28(9)：1671-1674.Liu Changjun, Zhang Weigang, Jiang Meng, et al.Study on Self-Induced Chirping for Fiber Bragg Grating[J].Acta Optica Sinica, 2008, 28(9)：1671-1674.

[8]黄力群，王 里，王 智，等.L波段掺铒光纤放大器的增益平坦滤波器设计[J].中国激光，2004, 31(7)：829-832.Huang Liqun, Wang Li, Wang Zhi, et al.Design on Gain-Flattening Filters of L-Band EDFAs[J].Chinese Journal of Lasers, 2004, 31(7) ：829-832.