运动TDMA系统目标时差定位算法❋
2011-06-28何子述
王 旭,何子述
(1.西南电子电信技术研究所,成都610041;2.电子科技大学电子工程学院,成都611731)
运动TDMA系统目标时差定位算法❋
王 旭1,2,何子述2
(1.西南电子电信技术研究所,成都610041;2.电子科技大学电子工程学院,成都611731)
根据时分多址(TDMA)系统的同步特征,利用TDMA运动目标准周期性信号的到达时间,提出了3种在三站时差定位系统中实现目标定位的算法。采用目标运动分析的方法,对TDMA目标位置的可观测性进行分析,提出了目标运动分析时差定位算法,利用目标航迹上多个位置的时差实现目标的定位。运用目标运动分析测距算法,提出了测距与传统时差定位和目标运动分析时差定位相结合的两种定位算法。3种定位算法充分利用了目标的运动特性,提高了TDMA目标的定位精度,避免了传统时差定位算法中的多解和无解现象。仿真结果验证了算法的有效性。
时分多址;无源定位;到达时差;目标运动分析
1 引言
无源定位技术因隐蔽性能强、作用距离远而获得了广泛应用。时差定位技术是利用目标信号到多个接收站的时间差,由多个双曲线(面)相交实现目标的定位。在多站时差定位系统中,三站时差定位系统在系统规模上容易实现,定位精度能够满足目标航迹估计的需要。三站时差定位系统能够实现二维空间目标的定位。三站时差定位算法需要求解非线性方程,常用的方法有Taylor展开法、两步最小二乘法、修正最小二乘法等[1-4]。由于3个站点的布站几何位置因素、噪声和测量误差的影响,三站时差定位存在多解和无解的现象[5,6],一般采用增加站点和数据融合的方法消除多解和无解现象[6,7]。
对于运动目标的定位,时差定位技术没有利用运动特性,只是在航迹跟踪算法(比如Kalman滤波器)中使用了运动模型。目标运动分析在单站目标定位中进行了广泛的研究,研究领域涉及运动参数可观测性[8-10]、定位算法[11,12]和观测站最优机动策略[13,14]等方面。目标运动分析的目的是利用信号到达时间、方位以及多普勒频偏等测量值对目标航迹进行估计。在目标运动分析中,一般利用了目标匀速运动和信号周期性的特征。一个实际的目标航迹可以认为是分段匀速运动。
时分多址(TDMA)通信系统是一个同步系统[15-17],TDMA目标(终端)发出时隙信号的时间与系统同步,并在每个时隙的起点,一般时隙信号的周期是固定的。TDMA系统是多目标共享无线信道,一个目标不能在每一个时隙都发出信息,因此可以认为一个TDMA目标的时隙信号具有准周期特性。利用准周期特性便能够对TDMA目标进行运动分析,实现包括目标位置在内的运动参数估计。
本文利用三站时差定位和目标运动分析相结合的方法,提出了3种二维空间TDMA运动目标定位的算法。第一种是目标运动分析时差定位算法(TDOA-M),利用信号到达3种接收站的时间差以及目标航迹上各信号到达同一个接收站的时间差,在三站时差定位系统中对二维空间的TDMA目标进行运动分析,实现目标的定位;第二种是传统时差定位与目标运动分析测距相结合的算法(TDOA-CM),传统两步最小二乘法的第一步是求出目标的距离,在TDOA-R算法中目标的距离由目标运动分析进行估计;第三种是目标运动分析时差定位与目标运动分析测距相结合的算法(TDOA-M-M),将运动目标分析时差定位分为测距和定位两个步骤,用目标运动分析测距测速算法实现距离的估计。在后续的仿真分析中验证了TDOA-M-M具有最好的定位性能。
2 TDMA目标时差定位模型
假设3个接收站位于R1(x01,y01)、R2(x02,y02)和R3(x03,y03),如果3个接收站接收到TDMA移动目标在位置Tk,Tk-1,…,Tk-N分别发出的N+1个信号,目标运动速度为(vx,vy),如图1所示。假设各信号对应的发射时间为tt(k-j)(j=0,1,2,…,N),第i个接收站对应的接收时间为tri(k-j)(i=1,2,3),TDMA系统的时隙信号的周期为Ts。

图1 运动目标三站时差定位Fig.1 Model of three-station TDOA location for moving targets
接收时间与发射时间的关系为

式中,i=1,2,3;j=0,1,…,N;c为电磁波的传播速度。目标在位置Tk-j到第i个接收站的距离rij为
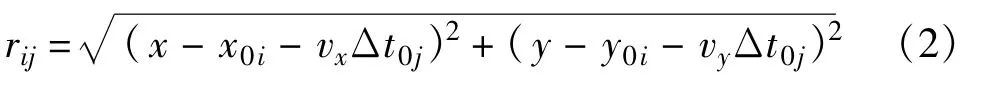
对于第1个接收站,目标在位置Tk-j和位置Tk-l的接收时间之差为

其中:
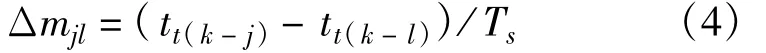
式(3)中r1j-r1l表示目标在位置Tk-j和位置Tk-l到接收站1的距离之差,一般远小于电磁波在信号周期Ts内传播的距离,在满足
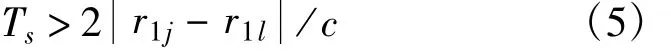
情况下有:

式中,round()为四舍五入函数。
由式(3),目标在位置Tk-j和位置Tk-l到接收站1的距离之差为

由式(4),目标在位置Tk-j和位置Tk-l信号发射时间之差为
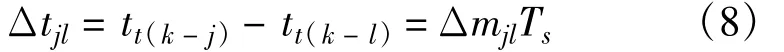
同理,可得目标在位置Tk-j和位置Tk-l到接收站2或接收站3的距离之差为

由式(1),目标在位置Tk-j到第1和第2个接收站的距离差为

目标在位置Tk-j到第1和第3个接收站的距离差为

式(7)、(9)和(10)为不同信号到同一接收站的距离差模型,式(11)和(12)为同一信号到两个接收站的距离差模型,式(8)为不同信号发射时间差模型。
3 目标运动分析时差定位算法
根据同一信号到接收站1和接收站2的距离差模型(11)有:

利用式(2):
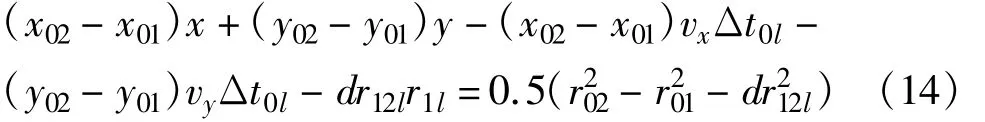
其中接收站到坐标原点的距离为
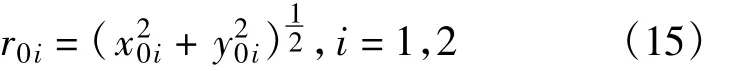
令
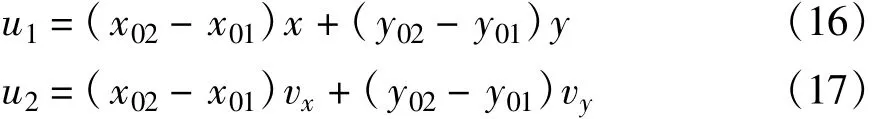
式(14)为
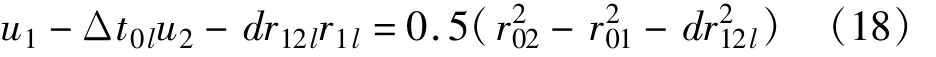
为求出目标位置Tk的距离,由式(7)有:

同理,对于同一信号到接收站1和接收站3的距离差模型(式(12)),令

在目标位置Tk-l处可得:

对于N+1个观测值,利用式(19)和式(22)可以建立2(N+1)个方程,矩阵形式如下:

其中:

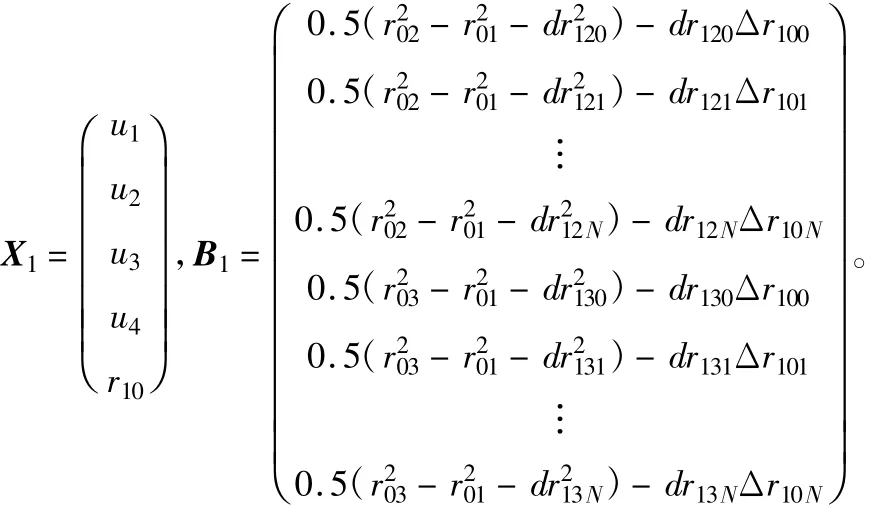
方程(23)有解的条件为A1的秩为5,即:

式(24)是在三站时差定位系统中目标距离可观测性条件,要求矩阵A1列满秩。
如果3个接收站在一条直线上,并且目标在3个接收站的延长线上运动,则目标距离是不可观测的,即式(24)不成立。在这种情况下,对任意l,dr12l和dr13l是接收站1到接收站2、3之间的距离,用dr12和dr13表示,都是常数,此时矩阵A1第5列与第1列、第3列线性相关,设A1i表示A1的第i列列向量,有:

因此,矩阵A1不是列满秩矩阵。这就证明了三站时差定位系统中匀速直线运动目标距离不可观测条件。
根据式(16)和式(20),目标定位的矩阵形式为

式(26)采用目标运动分析的方法实现运动目标的定位,称为目标运动分析时差定位算法(TDOA-M)。
根据式(17)和式(21)还可以求出目标运动速度分量。式(26)有解条件为

只要3个接收站不在一条直线上,即满足式(28)时,式(26)有解,能够对二维目标进行定位。式(27)是三站时差定位系统中目标位置可观测性条件。

4 三站测距测速算法
对于接收站1,将式(7)中r1l左移项、Δr1jl右移项、平方,有:

利用式(2),有:
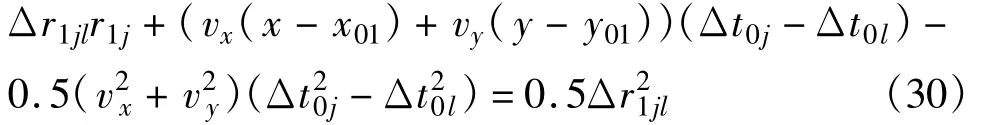
令

式中,v为目标运动的速度。由式(8)有:

式(30)可以变为
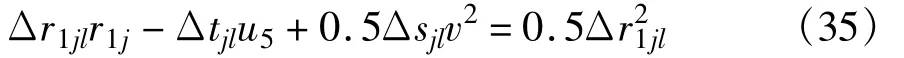
对任意j,当l∈(0,1,2,…,N)且l≠j时,可以建立N个以r1j为变量的方程组。对于接收站2,令

由式(9)有:

对于接收站3,令
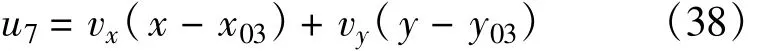
由式(10),有:

根据式(11),方程(37)中r2j用r1j表示,有:
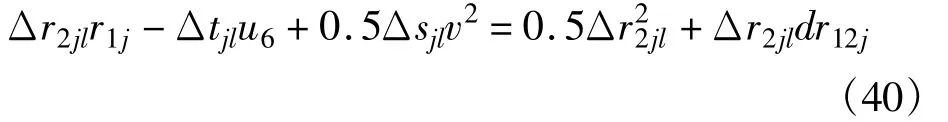
根据式(12),方程(39)中r3j用r1j表示,有:

对于N+1个观测值,用式(35)、(40)和(41)可以建立3N个方程,当j=0时求解r10,用矩阵形式表示为

其中:


方程(42)利用3个接收站的到达时间测量值实现了目标到第一个接收站的距离和运行速度的估计。当矩阵A3秩为5时,方程(42)有解,即:

5 通过测距的运动目标时差定位算法
对于目标位置Tk,传统时差定位算法为

式(44)的矩阵形式为

其中:

传统两步最小二乘法通过求解一元二次方程求解距离r10。在本文提出的传统时差定位与目标运动分析测距相结合的算法(TDOA-C-M)中,距离r10由目标运动分析算法式(42)给出。式(44)简称为TDOA-C-M算法。
在式(19)和式(22)中,将r10作为已知变量,有:
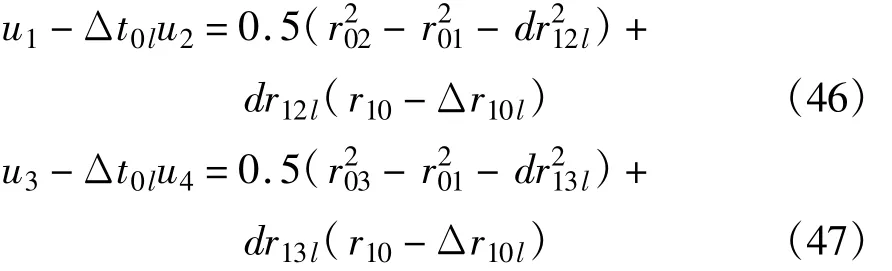
对于N+1个观测值,利用式(46)和式(47)可以建立2(N+1)个方程,矩阵形式如下:

其中:

将u1和u3代入式(26)便能够实现目标的定位,上式中距离r10由目标运动分析算法式(42)给出。该算法称为目标运动分析时差定位与目标运动分析测距相结合的算法(TDOA-M-M)。
6 运动目标时差定位仿真分析
假设3个传感器在平面坐标位于(0,0,0)、(20 000,5 000,0)和(-20 000,5 000,0),传感器位置坐标均方根误差3 m,距离差均方根误差30 m,目标系统同步均方根误差1μs。假设移动目标5 s发一个信号,但并不是每一个信号都用于距离估计,每间隔10个信号用于仿真分析。
假设目标在二维空间中平行于X轴由左向右飞行,匀速飞行速度为200 m/s。
6.1 目标距离估计仿真分析
本文提出了两种测距算法:X1r10(式(23))和X3r10(式(42))。X1r10利用目标航迹上各点到不同接收站的距离差进行测距,X3r10主要利用目标航迹上不同位置到同一个接收站的距离差进行测距。图2为距离估计仿真结果,图中Hr10表示传统时差的距离估计。
如图2所示,算法X3r10的精度最好,算法X1r10的精度好于算法Hr10。传统时差距离估计算法Hr10只利用了目标航迹上一个位置的数据进行估值,而X1r10和X3r10利用了所有位置上的数据,因此X1r10和X3r10的精度都高于Hr10。

图2 测距算法X1r1、X3r10和Hr10估计误差对比分析Fig.2 Range variances of X1r10,X3r10 and Hr10
6.2 时差定位仿真分析
仿真中对传统两步最小二乘法(TDOA-C)、目标运动分析时差定位算法(TDOA-M)、传统时差定位与目标运动分析测距相结合的算法(TDOA-CM)、目标运动分析时差定位与目标运动分析测距相结合的算法(TDOA-M-M)共4种算法进行了分析。图3和图4为4种算法定位精度仿真结果。定位精度用几何释度(GDOP)表示为

在图3中,传统时差定位算法TDOA-C的性能最差。传统时差定位算法中,采用目标运动分析的距离估计后,算法TDOA-C-M的性能好于TDOA-C。算法TDOA-M-M的性能最好。
图4用于比较算法TDOA-M和TDOA-M-M的定位性能。在算法TDOA-M-M中,采用了X3r10测距算法,其定位精度要好于TDOA-M。

图3 算法TDOA-C、TDOA-M-M和TDOA-C-M定位精度分析Fig.3 GDOPs of TDOA-C,TDOA-M-M and TDOA-C-M

图4 算法TDOA-M和TDOA-M-M定位精度分析Fig.4 GDOPs of TDOA-M and TDOA-M-M
7 结束语
本文利用目标运动特性,根据3个观测站接收到的目标周期性信号的到达时间,对二维目标的定位算法进行了研究,主要结论如下:
(1)采用目标运动分析的时差定位算法好于传统的时差定位算法。
(2)在定位算法中都需要对目标的距离进行估计,距离估计精度确定了定位精度。算法TDOA-M能够同时实现含目标位置、速度分量的中间变量以及目标距离的估计,算法TDOA-C、TDOA-C-M和TDOA-M-M先求取目标距离,再实现定位。
[1] Foy W H.Position location solutions by Taylor series estimation[J].IEEE Transactions on Aerospace and Electronic Systems,1976,12(2):187-194.
[2] Julius O Smith,Jonathan S Abel.Closed-form leastsquares source location estimation from range-difference measurements[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1987,35(12):1661-1669.
[3] Chart Y Ho K C.A simple and efficient estimator for hyperbolic location[J].IEEE Transactions on Signal Processing,1994,42(8):1905-1915.
[4] Huang Z,Lu J.Total least squares and equilibration algorithm for range difference Location[J].Electronics Letters,2004,40(5):12l-122.
[5]俞志强,叶朝谋.四站三维时差定位模糊分析[J].空军雷达学院学报,2009,23(5):370-372.
YU Zhi-qiang,YE Chao-mou.Analysis of Ambiguity of 4-Station 3D TDOA Positioning[J].Journal of Air Force Radar Academy,2009,23(5):370-372.(in Chinese)
[6]叶朝谋,俞志强.三维时差定位系统的模糊及无解分析[J].现代电子技术,2009,23(5):22-24,27.
YE Chao-mou,YU Zhi-qiang.Study on Ambiguity and Non-solution of 3-D TDOA Location Systems[J].Modern Electronic Technique,2009,23(5):22-24,27.(in Chinese)
[7]陈玲,李少洪.可消除定位模糊的无源时差定位算法[J].北京航空航天大学学报,2005,31(1):89-93.
CHEN Ling,LI Shao-hong.Passive TDOA location algorithm for eliminating location ambiguity[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(1):89-93.(in Chinese)
[8] Nordone S C,Aidala V J.Observability Criteria for Bearings-Only Target Motion Analysis[J].IEEE Transactions on Aerospace and Electronic Systems,1981,17(2):162-166.
[9] FOGEL ELI,GA VISH MOTTI.Nth-order dynamics target observability from angle measurements[J].IEEE Transactions on Aerospace and Electronic System,1988,24(3):305-308.
[10] Song T L.Observability of Target Tracking with Bearingonly Measurements[J].IEEE Transactions on Aerospace and Electronic System,1996,32(4):1468-1472.
[11] Nordone S C,Marcus L G.A closed-form solution to bearing-only target motion analysis[J].IEEE Journal of Oceanic Engineering,1997,22(1):168-178.
[12] Moon J R,Nordone S C.An Approximate Linearization approach to bearing-only Target Tracking[J].IEEE Transactions on Aerospace and Electronic Systems,2000,36(1):176-188.
[13] Fawcett J A.Effect of course maneuvers on bearings-only range estimation[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1988,36(8):1193-1199.
[14] Hammel S E,Liu P T,Hilliard E J,et al.Optimal observer motion for localization with bearings measurements[J]. Computer and Mathematics with Applications,1989,18(1-3):171-186.
[15] Lee K D,Chang K N.A real-time algorithm for timeslot assignment in multi-rate retern channels of interactive satellite multimedia networks[J].IEEE Journal on selected areas in communications,2004,22(3):518-528.
[16]刘丽宏,李维,刘海建.TDMA帧结构研究[J].无线电通信技术,2007,33(4):5-7.
LIU Li-hong,LI Wei,LIU Hai-jian.Research on TDMA Frame Structure[J].Radio Communications Technology,2007,33(4):5-7.(in Chinese)
[17]秦勇,张军,张涛.TDMA时隙分配对业务时延性能的影响分析[J].电子学报,2009,37(10):2277-2283.
QIN Yong,ZHANG Jun,ZHANG Tao.Effect of TDMA Timeslot Assignment on Traffic Delay[J].Acta Electronica Sinica,2009,37(10):2277-2283.(in Chinese)
W ANG Xu was born in Shehong,Sichuan Province,in 1964.He received the M.S.degree in Xidian University in 1988.He is currently working toward the Ph.D.degree.His research interests include target passive location,communication and array signal processing,etc.
Email:wangxu64@sina.com
何子述(1962-),男,四川新繁人,博士,电子科技大学电子工程学院教授、博士生导师,主要从事目标无源定位、相控阵技术、MIMO雷达技术、宽带数字阵等的研究。
HE Zi-shu was born in Xinfan,Sichuan Province,in 1962.He is now a professor with the Ph.D.degree and also the Ph.D.supervisor.His research interests include target passive location,phasedarray technology,MIMO radar and wide-band digital array,etc.
Email:zshe@uestc.edu.cn
TDOA Location Algorithms for Moving TDMA Target
WANG Xu1,2,HE Zi-shu2
(1.Southwest Electronics and Telecommunication Technology Research Institute,Chengdu 610041,China;2.Department of Electronic Engineering,University of Electronic Science and Technology of China,Chengdu 611731,China)
According to the time synchronization property of time division multiple access(TDMA)system,three location algorithms are proposed based on the measurements of time of arrival(TOA)of TDMA moving target.The method of target motion analysis(TMA)is used to analyse the observability condition of target position and realize the TMA time difference of arrival(TDOA)location(TDOA-M for short).Other two joint algorithms of conventional TDOA location(TDOA-C)and TDOA-M with TMA ranging algorithm are presented.The proposed algorithms make full use of the target motion property to improve location precision and avoid the phenomenon of multiple solutions and no solution.The simulation results illustrate the validity of the proposed algorithms.
time division multiple access(TDMA);passive location;TOA;target motion analysis(TMA)
TN953
A
10.3969/j.issn.1001-893x.2011.04.011
王旭(1964-),男,四川射洪人,1988年于西安电子科技大学获硕士学位,现为电子科技大学博士研究生,主要研究方向为目标无源定位、通信信号处理、阵列信号处理等;
1001-893X(2011)04-0048-06
2011-03-01;
2011-04-11
