混沌噪声产生器及其FPGA实现❋

王喜风，王可人，冯 辉，田上成

（解放军电子工程学院，合肥230037）

混沌噪声产生器及其FPGA实现❋

王喜风，王可人，冯 辉，田上成

（解放军电子工程学院，合肥230037）

为实时产生混沌噪声，设计了一种基于Tent映射双向耦合映象格子和“接收－拒绝”法的混沌噪声产生器，将其由浮点运算转换为定点运算后在FPGA上实现。所实现的混沌噪声产生器具有结构简单、运算复杂度低、资源占用少且易于控制等优点。性能测试结果表明：混沌噪声产生器能够产生具有任意分布和平坦功率谱的混沌噪声，且随机性较好。

混沌噪声；耦合映象格子；“接收－拒绝”法；FPGA

1 引言

传统噪声多由模拟噪声源产生，易受温度和其它环境因素影响而发生漂移，且可控性差，难于对其进行加工和复制［1］。随着数字电路的发展，数字化噪声逐渐取代模拟噪声，但现有的多种产生方法都有其缺陷：m序列的随机性较差，数量有限；多频选择调相方式和直接序列移相键控方式产生的信号频谱不满足白噪声的要求［1］。

混沌信号具有类噪声性、带宽较宽、可控性和可再生性等优点，可以替代以上方法来产生数字化噪声信号。

本文基于Tent映射双向耦合映象格子（Tent Double-way Coupled Map Lattice，TDCML）和“接收－拒绝”法提出了一种混沌噪声产生方法，并将该产生方法在FPGA上实现为混沌噪声产生器。对实际产生的混沌噪声序列进行性能测试，并与相应的理论值和仿真结果进行了比较，结果表明混沌噪声产生器能够产生具有任意分布和平坦功率谱的混沌噪声，且结构简单，易于控制。

2 混沌噪声的产生

与低维的混沌映射相比，TDCML映射在时间和空间上都是混沌的，具有更复杂的混沌行为和更丰富的混沌特性，通过序列间的相互扰动可以有效克服有限精度问题，同时不影响序列本身的混沌特性［2］。另外，TDCML映射运算简单，数据间没有乘除运算，且其并行运算的特点使序列的产生速度更快［3］，所以本文采用TDCML映射作为混沌噪声源。

2．1 TDCML映射

TDCML映射的数学表达式［4］为

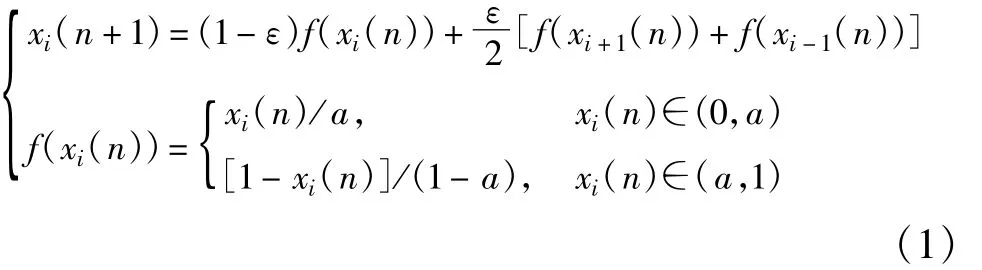
式中，ε是耦合系数且0＜ε＜1，L是系统尺寸，i为格点坐标，n为迭代次数，a是局部映射（Tent映射）的分形参数且0＜a＜1，边界条件为x0（n）＝xL（n），xL＋1（n）＝x1（n）。

TDCML映射在ε＜0.01时，各格点序列分布趋于均匀分布，而其局部映射（Tent映射）对扰动极为敏感，微小的扰动在格子间通过扩散而迅速放大，因此，在弱耦合情况下（ε＝0.01），TDCML映射仍具有良好的时空混沌性态［4］。另外，由于局部映射的功率谱是常数，所以TDCML映射各格点序列具有平坦的功率谱。

2．2 混沌噪声的产生

常用于产生高斯分布信号的算法有Box－Muller算法和Wallace算法等，这些算法只能产生特定分布的信号，且有数据间乘法运算［5］，影响信号的产生速度。文献［6］提出的“接收－拒绝”法可以产生任意分布的随机数，且算法简单，随机数产生速度快。由此，本文采用TDCML映射和“接收－拒绝”法提出了一种产生具有任意分布和平坦功率谱的混沌噪声设计方法，图1为其设计框图。

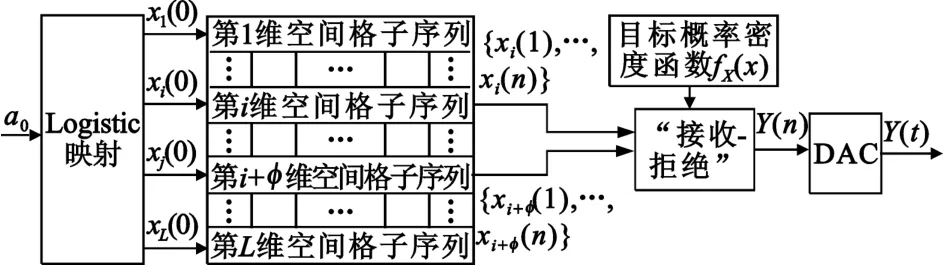
图1 混沌噪声产生器的设计框图Fig.1 Design block diagram of chaotic noise generator

在弱耦合情况下，TDCML映射的各格点序列都满足均匀分布，为减少数据间的相关性，选取TDCML映射中空间间隔为φ、长度为n的两个格点序列｛xi（1），xi（2），…，xi（n）｝和｛xi＋φ（1），xi＋φ（2），…，xi＋φ（n）｝，通过“接收－拒绝”法产生具有任意分布和平坦功率谱的混沌序列Y（n），将Y（n）经DAC后得到混沌噪声Y（t）。为便于控制，TDCML映射的L个初始值由Logistic映射提供，这样只要一个Logistic映射的初始值a0就可以驱动整个系统运行。

3 混沌噪声的FPGA实现

3．1 TDCML映射的定点运算模型

为降低资源占用率，提高运算速度，将式（1）由浮点运算转换为定点运算。经仿真分析，当p＝32时TDCML序列处于混沌态且性能较好，所以混沌噪声产生器在FPGA上实现时的计算精度取32 bit。为避免全同步现象［7］，考虑在降低资源占用率的同时提高序列性能，系统尺寸L取8。

为产生均匀分布的混沌序列，同时简化FPGA的定点运算，令ε＝2－7＝0.007 812 5，a＝0.5。此时，TDCML映射的定点运算模型为

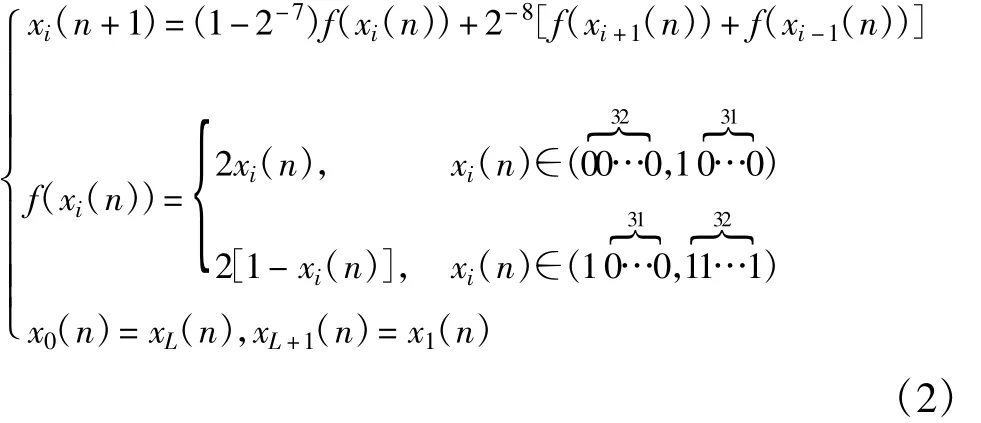
该模型中只有移位、加法、减法和判断等简单运算，所以占用资源少，信号产生速度快。

3．2 混沌噪声产生器

本文采用Xilinx公司的Spartan 3E系列的XC3S1600E芯片，以产生具有Gauss分布和平坦功率谱的混沌噪声为例来实现本文提出的混沌噪声产生方法。图2为该混沌噪声产生器的系统框图。

图2 混沌噪声产生器的系统框图Fig.2 System block diagram of chaotic noise generator

当FPGA的计算精度为32 bit、TDCML映射的系统尺寸L＝8、耦合系数ε＝2－7、分形参数a＝0.5时，该系统的工作流程如下。

（1）由于Logistic映射的数据产生周期为3个时钟周期，为减少相邻数据间的相关性，抽样器每间隔6个时钟周期抽取一次数据。

（2）在计数器控制下，串并转换器依次将抽样器输出的8个32 bit数据存储到寄存器中，到最后一个数据存储到寄存器为止，总共需要48个时钟周期，系统在计数器下一次计数时触发8个数据同时并行输出。

（3）当初值选择器第一次接收到数据时，将选通串并转换器传来的数据作为TDCML产生器的初始值，之后选通TDCML产生器传来的数据，让TDCML产生器循环迭代产生TDCML序列，图3为TDCML映射的算法流程图。

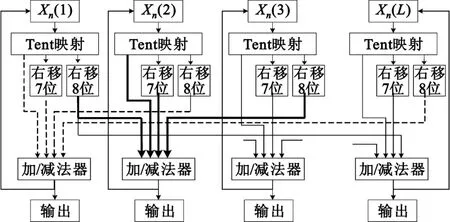
图3 TDCML映射的算法流程图Fig.3 Flow chart of TDCML-map arithmetic

（4）选取TDCML映射格点坐标是3和6的两路32 bit数据，将其输出到接收－拒绝模块，图4为“接收－拒绝”模块框图。ROM中预先存储了Gauss分布数据，将第3路的高10 bit作为地址码读取ROM中1 024个32 bit的分布数据，将其与第6路的数据进行比较，当a＜b时，控制模块使能FIFO的wr－en，将第3路的32 bit数据存入FIFO。当FIFO存储一定数据后，在接收数据的同时，控制模块使能rd－en，在clk－out时钟的控制下将存储的数据输出，得到混沌噪声序列Y（n），最后通过DAC将混沌噪声Y（t）输出。

另外，为保证FIFO的连续输出，根据“接收－拒绝”法原理［5］，若产生Gauss分布信号，设定clk－out＝1／21 clk，clk－in＝1／7 clk，即在主频100 MHz下，混沌噪声的输出速度是4.76 Msample／s。为更好体现分布数据的分布特点，本文对Gauss分布数据采用μ律量化后存储到ROM中。此外，为提高系统的可控性，本文设计了一个初值赋值模块，只需一个初始值a0就能驱动整个系统运行。

图4 “接收－拒绝”模块框图Fig.4 Block diagram of“acceptance-rejection”module

利用ISE Simulator对混沌噪声产生器进行功能仿真，当初始值a0＝1时，仿真结果如图5所示。可见，混沌噪声连续输出且信号产生速度符合设计要求。

图5 ISE Simulator功能仿真结果Fig.5 Functional simulation result with ISE simulator

4 性能测试与结论

本节对混沌噪声产生器产生的混沌伪随机序列Y（n）进行性能测试［8－9］，主要包括不变分布、功率谱和最大Lyapunov指数。本文选取满足Gauss分布和Rayleigh分布的两种混沌噪声序列进行测试。

4．1 Gauss分布混沌噪声序列性能测试

在ROM中预存1 024个32 bit的服从N（0，1）分布的数据。设混沌噪声产生器的初始值a0＝1，取其产生的50 000个样本数据进行不变分布和功率谱测试，图6为样本数据的不变分布直方图和功率谱图。

可见，该样本数据的直方图包络很好地逼近标准Gauss分布概率密度曲线，其功率谱没有较大的峰值，较平坦，同时计算得到样本数据的均值为0.001 2，方差为0.997 1，与标准Gauss分布的均值和方差的理论值非常接近。可见混沌噪声产生器能够按照ROM中存储的Gauss分布数据产生具有相应分布和平坦功率谱的混沌噪声。

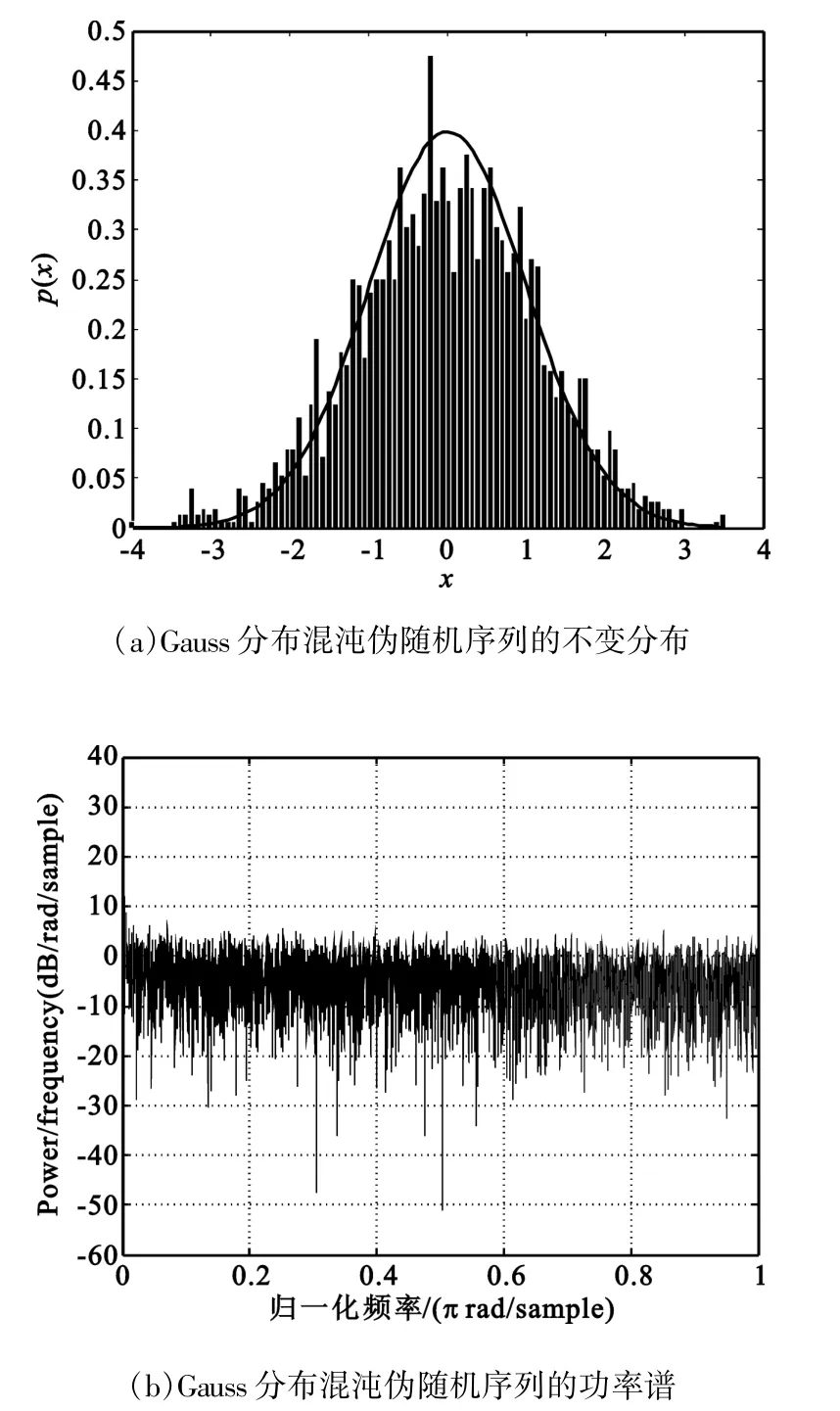
图6 Gauss分布混沌伪随机序列的性能测试Fig.6 Performance testing of chaotic pseudo sequences with Gauss distribution

混沌噪声作为一种类噪声，其随机性是衡量其性能好坏的一个重要指标。混沌信号的随机性通常采用最大Lyapunov指数来衡量，最大Lyapunov指数越大，随机性越强。

本文采用小数据量法来计算Gauss分布混沌伪随机序列的最大Lyapunov指数，当嵌入维数m＝3、时延τ＝3时，Gauss分布混沌伪随机序列的最大Lyapunov指数为2.806 9，远远大于低维混沌序列的最大Lyapunov指数，所以Gauss分布混沌伪随机序列具有良好的随机性。

4．2 Rayleigh分布混沌伪随机序列性能测试

在ROM中预存1 024个32 bit的Rayleigh分布数据，该Rayleigh分布服从R（2）分布，设混沌噪声产生器初始值a0＝1，取其产生的50 000个样本数据进行不变分布和功率谱测试，图7为样本数据的不变分布直方图和功率谱图。

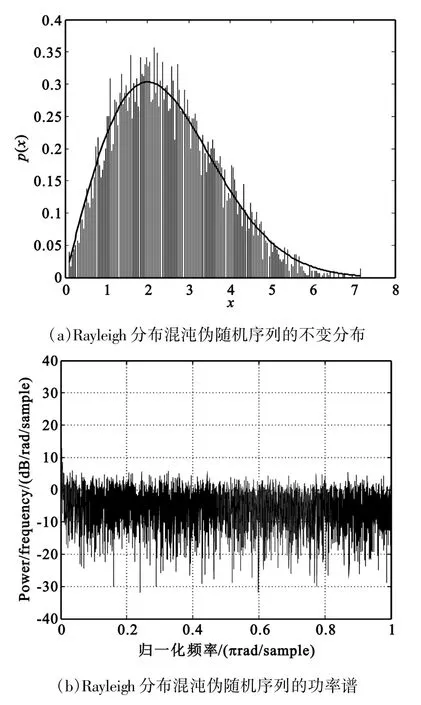
图7 Rayleigh分布混沌伪随机序列的性能测试Fig.7 Performance testing of chaotic pseudo sequences with Rayleigh distribution

可见，样本数据的直方图包络很好地逼近服从R（2）分布的Rayleigh分布概率密度曲线，其功率谱没有较大的峰值，较平坦。计算得到样本数据的均值为2.456，方差为1.732，与理论上的均值和方差8－2π很接近。同样，混沌噪声产生器能够按照ROM中存储的Rayleigh分布数据产生具有相应分布和平坦功率谱的混沌噪声。

当嵌入维数m＝3、时延τ＝3时，Rayleigh分布混沌噪声序列的最大Lyapunov指数为2.840 9，远远大于低维混沌序列的最大Lyapunov指数，所以Rayleigh分布混沌噪声序列具有良好的随机性。

综上所述，混沌噪声产生器能够按照ROM中的分布数据产生具有相应分布和平坦功率谱的混沌噪声，且该信号具有较强的随机性。

4．3 设计方法比较

采用XC3S1600E芯片，在100 MHz主频下，以产生Gauss分布混沌噪声为例，将本文的混沌噪声产生器的设计方法与文献［1］中两种基于Logistic映射产生混沌噪声的设计方法进行比较，结果如表1所示。

表1 设计方法比较Table 1 Comparison of design methods

由表1可见，设计方法1资源占用较多，几乎是本文方法的2倍，特别是乘法器已经超过芯片资源的1倍，但是其最大输出速度是本文方法的近7倍；本文方法的最大输出速度是设计方法2的近3倍，但资源占用是其近5倍；3种方法产生的Gauss分布的分布特性基本相同；本文方法最多能产生4路混沌噪声，而设计方法1和2只能产生1路信号。

［1］张家树，冯海涛.基于混沌的最佳压制干扰噪声源设计［J］.电波科学学报，2006，21（5）：701－707.

ZHANG Jia－shu，FENG Hai－tao.Chaos－based optimal radar jamming noise sources design［J］.Chinese Journal of Radio Science，2006，21（5）：701－707.（in Chinese）

［2］ Hu Hanping，Xu Ya，Zhu Ziqi.A method of improving the properties of digital chaotic system［J］.Chaos Solitons and Fractals，2008，38（2）：439－446.

［3］ Ping Li，Zhong Li，Wolfgang A Halang，et al.A multiple pseudorandom－bit generator based on a spatiotemporal chaotic map［J］.Physics Letters A，2006，349（6）：467－473.

［4］刘建东，付秀丽.基于耦合帐篷映射的时空混沌单向Hash函数的构造［J］.通信学报，2007，28（6）：30－38.

LIU Jian－dong，FU Xiu－li.Spatiotemporal chaotic one－way Hash function construction based on coupled tent maps［J］.Journal on Communications，2007，28（6）：30－38.（in Chinese）

［5］杜学峰，武杰.基于FPGA的任意分布高速伪随机数发生器［J］.中国科学技术大学学报，2006，36（9）：990－994.

DU Xue－feng，WU Jie.Arbitrary distribution high－speed pseudo－random number generator based on FPGA［J］.Journal of University of Science and Technology of China，2006，36（9）：990－994.（in Chinese）

［6］ Mao Y，Liu C，Liu W.Design and FPGA implementation of a pseudo－random bit sequence generator using spatiotemporal chaos［C］／／Proceedings of 2006 International Conference on Communications，Circuits and Systems.Guilin：IEEE，2006：2114－2118.

［7］曹骝，毛耀斌，刘文波，等.时空混沌伪随机比特发生器及其FPGA实现［J］.系统工程与电子技术，2008，30（9）：1606－1610.

CAO Liu，MAO Yao－bin，LIU Wen－bo，et al.Pseudorandom bit generator based on spatio－temporal chaos and its FPGA implementation［J］.Systems Engineering and Electronics，2008，30（9）：1606－1610.（in Chinese）

［8］杨瑛，邓鹏飞，刘春泉.混沌噪声调频信号对UWB－SAR／ISAR成像的干扰［J］.电讯技术，2008，48（9）：75－78.

YANG Ying，DENG Peng－fei，LIU Chun－quan.Chaotic Noise FM signal jamming on UWB－SAR／ISAR Imaging［J］.Telecommunication Engineering，2008，48（9）：75－78.（in Chinese）

［9］吕波，张晓发，袁乃昌.数字噪声宽带干扰源设计［J］.军械工程学院学报，2008，20（1）：54－57.

LV Bo，ZHANG Xiao－fa，YU Nai－chang.Design of digital noise FM broadband jamming source［J］.Journal of Ordnance Engineering College，2008，20（1）：54－57.（in Chinese）

W ANG Xi－feng was born in Jiashan，Zhejiang Province，in 1986.He received the B.S.degree from Electronic Engineering Institute of PLA in 2008.He is now a graduate student.His research interests include nonlinear signal processing and digital system design.

Email：wangxifeng815＠163.com

王可人（1957-），男，江苏镇江人，1986年于解放军理工大学获硕士学位，现为教授、博士生导师，主要研究方向为无线通信信号的分析和处理；

WANG Ke－ren was born in Zhenjiang，Jiangsu Province，in 1957.He received the M.S.degree from PLA University of Science and Technology in 1986.He is now a professor and also the Ph.D. supervisor.His research interests include wireless communication signal analysis and processing.

冯辉（1978-），男，山东荣城人，2009年于解放军电子工程学院获博士学位，现为讲师，主要研究方向为通信信号处理；

FENG Hui was born in Rongcheng，Shandong Province，in 1978.He received the Ph.D.degree from Electronic Engineering Institute of PLA in 2009.He is now a lecturer.His research direction is communication signal processing.

田上成（1985-），男，河北故城人，2008年于合肥工业大学获学士学位，现为硕士研究生，主要研究方向为通信信号处理、卫星通信技术。

TIAN Shang－cheng was born in Gucheng，Hebei Province，in 1985.He received the B.S.degree from Hefei University of Technology in 2008.He is now a graduate student.His research interests include communication signal processing and satellite communication technology.

Chaotic Noise Generator and its FPGA Realization

WANG Xi-feng，WANG Ke-ren，FENG Hui，TIAN Shang-cheng
（Electronic Engineering Institute，Hefei 230037，China）

To generate chaotic noise，a chaotic noise generator is designed based on Tent double-way coupled map lattice and“acceptance-rejection”.The generator is realized on FPGA after it is converted from floating pointed operation to fixed pointed operation.The realized generator has advantages including simple structure，low complexity of algorithm，accounting for few resources and easy control.The results of performance test show that the generator can generate chaotic noise with arbitrary distribution，flat power spectrum and good randomicity.

chaotic noise；coupled map lattice；“acceptance－rejection”method；FPGA

TN97

A

10.3969／j.issn.1001－893x.2011.04.006

王喜风（1986-），男，浙江嘉善人，2008年于解放军电子工程学院获学士学位，现为硕士研究生，主要研究方向为非线性信号处理和数字系统设计；

1001－893X（2011）04－0026－05

2011－01－13；

2011－03－03