雷达信号检测中解模糊的改进算法
2011-06-28韩红波
韩红波
(海能达通信股份有限公司,深圳518057)
0 引 言
脉冲多普勒雷达发射的脉冲频率有一定的范围,它的测量数据会有一定的限制,所以总会存在着模糊问题。当目标的回波延迟时间大于发射脉冲的重复周期时,采用高、中脉冲重复频率(PRF)的脉冲多普勒雷达会产生距离模糊。为了避免模糊现象,一般采用多重PRF工作方式的雷达系统[1]。
多重PRF工作方式的雷达解模糊常用的算法有一维集算法和查表法。其中,查表法计算简单,但对于单个重复频率下的测量精度要求较高;而一维集算法的解模糊精度很高但它的计算量很大[1,4]。基于此,本文提出了一种基于一维集算法的解距离模糊的改进算法,该算法吸收查表法思想,其运算速度大大提高,同时又有较强的纠错能力。
1 常用解距离模糊的算法
采用多重脉冲重复频率解模糊的原理是孙子定理。为了消除模糊,雷达系统成组的改变PRF,并得到一组相关测量值,即:
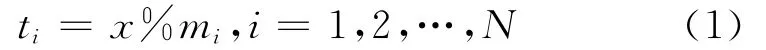
式中:x为真实距离;mi为脉冲重复周期;ti为相应脉冲重复周期上的测量值。
x、mi和ti都是以距离门为单位,共有N重脉冲重复周期,%表示求余运算。令t= (t1,…,tN),并称t为距离观测矢量,m= (m1,…,mN),称为模矢量。
1.1 孙子定理算法
孙子定理[1]:设m1,…,mk是两两即约的正整数,那么,对任意整数a1,…,ak,一次同余方程组:

必有解,且解数为1。事实上,同余方程组的解是:
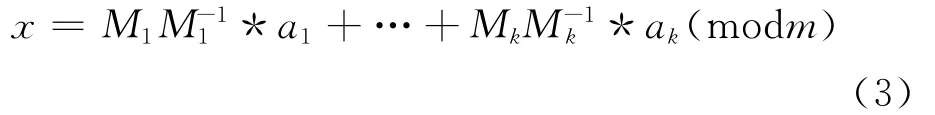
式中:m=m1…mk,Mj=m/mj(1≤j≤k),而是满足式(4)的一个整数:
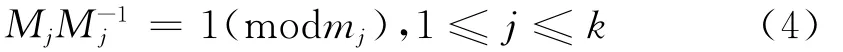
1.2 一维集算法[2]
一维集算法的实质是利用穷举法解同余方程组,算法基本原理:首先,对于每个测量值Ri(注意,Ri可能是1个距离单元的若干分之几),列出它所对应的全部可能的距离:

式中:Ri为第i个PRF对应的不模糊距离;Rui为第i重PRF对应的距离单元数;Rmax为雷达的最大作用距离。
由m个模糊的测量值产生的全部距离自小到大排队,并用Roi表示。m个顺序距离的平均平方误差为:
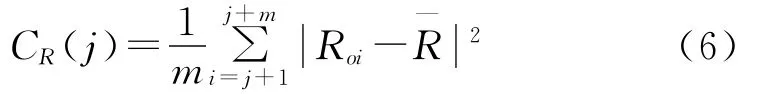
在CR(j)为最小的j值点上有最佳集出现,它可将所有可能的不模糊距离值正确解出。
1.3 查表法
余差查表法[3,5]是利用目标在各重脉冲重复周期(PRT)上的余数(模糊距离)之差(可为负值)进行解模糊。此方法选择其中一重PRT,以目标在该PRT上的余数作为基准,将其它各重PRT上的余数与基准相减,所得之差作为查找表中的查找项。其原理如图1所示。
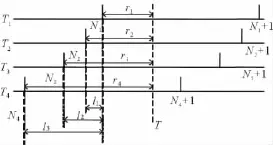
图1 余差查表法原理示意图
以四参差PRT的系统为例,由图1可见,以Ti(i=1,2,3,4)为重复周期,当目标处于某距离单元T(真实距离)时,它在各重PRT上的余数ri(即模糊距离)为:
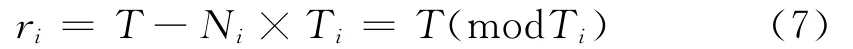
式中:i=1,2,3,4,Ni为模糊的PRT数(整型模糊数);mod(·)为求余数运算。
以Ti为基准可以求得Ni,因此有:
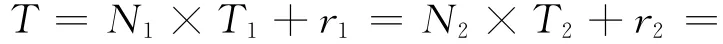

可以证明,当N1,N2,N3,N4为最小的互质整数时,它们与T是唯一对应的。即当选取适当的PRT组合,以保证N1,N2,N3,N4能够互质的情况下,如果测得目标在各重PRT上的余数,就可以唯一地求出目标的真实距离T。
比较3种算法,孙子定理可以给出真实距离和观测矢量间的解析关系,因此运算速度很快,但是孙子定理要求PRT两两即约,如果观测矢量存在误差,则计算结果的误差会很大;一维集算法有较强的误差纠错能力,但运算量大;查表法事先存储已建好的表,大大减少了运算量。
2 改进算法
本算法的思想是对一维集算法中花费运算时间的部分(即对所有可能距离的排序部分)进行改进。本算法中采用查表法的思想,首先对各重频的所有可能距离值进行建表存好,之后在计算的过程中,只要在表值上加上模糊距离即可。
2.1 算法的实现过程
假设通过n重频解模糊,脉冲重复周期为T1,T2,…,Tn,各重复周期对应的最大无模糊距离是Ru1,Ru2,…,Run,此时雷达最大探测距离为Rmax。
(1)首先选重频基数最小的重复周期作为基准周期,这里假设min(Ti)=T1,i=1,2…n。列出基准周期对应的所有目标距离可能值:
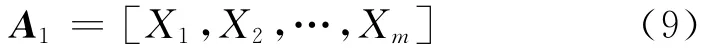
式中:Xi=i×Ru1,i=0,1,…,m,m=INT(Rmax/Ru1)为最大模糊度。
将其它非基准周期的最大不模糊距离所对应目标的所有可能距离值同样算出:
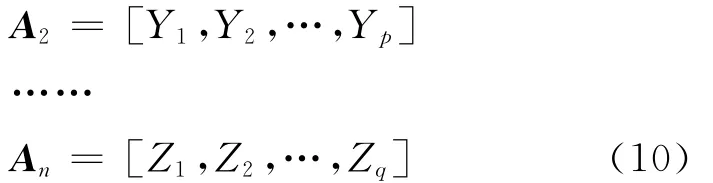
式中:Yi=i×Ru2,i=1,2,…,p,p=INT(Rmax/Ru2);Zi=i×Run,i=1,2,…,q,q=INT(Rmax/Run)。
由于T1是所有重复周期中的最小周期,所以必有m是所有模糊度中最大的一个,即m>p,…,m>q。
(2)将各组重频的所有目标可能距离值建表,表的行数为重频数n,列数为模糊度的最大值m。列数不为m的重频按一定准则对目标距离进行复制重新排列,得到表R。此时除了基准重频,其他重频中必然有相同的距离值,每一列对应的是同一距离单元。
(3)将信号回波中各个重频上的模糊距离值与表中各个重频上最大不模糊距离的所有可能距离值进行相加,得到一个新表R_new。这时表中得到的是各重频上目标的所有可能距离值。此时必然有某一列上的距离非常相近,此距离就为目标的真实距离。
(4)求表中各重频与基准重频之间差值的绝对值:
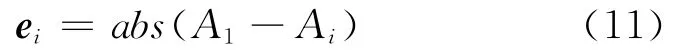
式中:i=1,2…n,ei是一个1×n的向量。
(5)求第4步中ei各列的对应项之和。
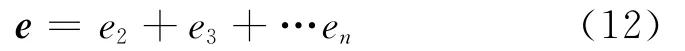
求行向量e中的最小值E,并记录位置k,当E小于某一个门限值时,就认为找到了目标的真实距离。在新表中相应位置的值就是目标的真实距离值,位置k-1就为模糊度。为了减小误差,目标的真实距离取该列和的平均值,即:
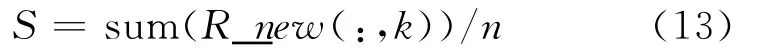
式中:sum(·)为求和运算;R_new(:,k)为新建表R_new中第k列的任意行。
2.2 算法的性能分析
算法速度方面,本文中改进算法的计算量要远小于一维集算法。一维集算法穷举了所有重频测量值对应的所有可能距离值,接着要对所有值排序,最后需要求出所有相邻的n个值的方差。当可能值较多时,一维集法对所有可能值排序就有很大的计算量。即使不考虑排序问题,仅求所有相邻n个值的方差计算量为次加法,次乘法。新算法是使用查表的一种方法,所以运算中同余差查表法一样,没有乘法运算,只有加法运算。而新算法比余差查表法多计算了n×m次加法运算。所以从运算量上,改进算法要比一维集算法少得多,比余差查表法稍多。
解模糊能力方面,当测量值有一定的误差时,改进算法能正确地解模糊,有较强的解模糊能力。但是当测量值有较大误差时,利用新算法解模糊可能出现错误。实际上若误差较大,一维集算法和余差法也有错解的情况。解模糊允许的最大测量误差、错解率与系统工作的PRF是密切相关的。PRF的选择是脉冲多普勒(PD)雷达的一个关键问题,它对测距性能有很大的影响。若雷达PRF选择不当,将导致距离遮挡变得严重,解模糊错解率上升。实际系统经常能提供多种重复频率。对于查表法,若查找表中没有某个重频的表值信息,就不能调用这组重频解模糊。
2.3 改进算法解距离模糊的实例仿真
某雷达以三重频解模糊,为了方便说明,选各重复周期对应的距离单元分别为T1=2、T2=3、T3=5,雷达的最大作用距离是30距离单元。
首先建表,建表步骤:
(1)选重频距离单元中最小的1个值为基准重频,本例中为2,列出其对应的所有可能距离。

表1 基准重频对应的所有可能距离值

表2 非基准重频对应的所有可能距离值
(3)将2中的两行按一定的原则将某些数复制后排列。
原则:比较其他重频距离与基准距离的关系,将其他重频中的距离值a放在基准重频中出现的第1个大于等于a对应的位置。
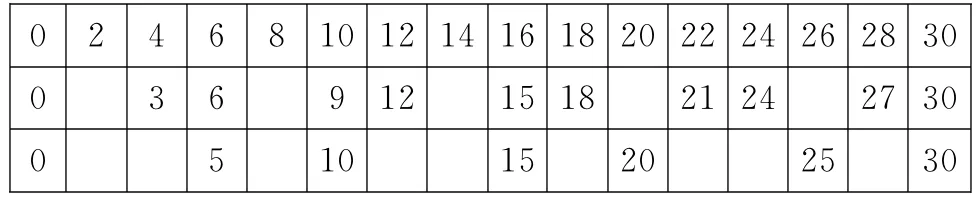
表3 非基准重频的所有可能距离值对应排列
(4)第3步结束后表中会有空余项,填充空余项。每空记录为本重频中的前一个距离值。

表4 非基准重频的某些可能距离值的复制
此时表建立完成。
其次,解模糊。设某目标在3个重频上得到的测量值为t1=1,t2=1,t3=3,将3个测量值加到表中得到1个新表,表5中的值就是该目标的所有可能距离值。

表5 某目标的三种重频可能的真实距离
求各列中相互间差值,找到最小一项,在无误差情况下,此项差值必然全部为0。在有误差情况下,若相互间差值的绝对值之和小于某给定允许值即认为此处为真实值。本例中找到距离值13。
本方法要注意的是加在事先建的表上的值不一定是模糊距离值。该方法中,当t1>t2时,要取t2=t2+T2;t1>t3时,要取t3=t3+T3。其中Ti为脉冲重复频率对应的距离单元。
图2给出该算法的解模糊正确率仿真图。
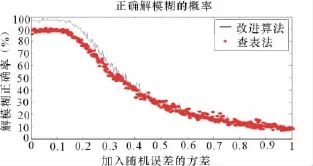
图2 误差大小对新算法正确率的影响
由图2可见新算法较查表法解模糊纠错率更高,从性能分析中知其速度要比一维集算法快很多。
3 结束语
本文提出的基于一维集算法的改进算法有很好的纠错能力,但运算速度远远大于一维集算法,故它的适应能力强于孙子定理法,实时性能好于一维集算法。由于这种算法是一维集算法的一个变体,所以它还可用于解速度模糊,在多目标情况下能有效地进行目标匹配,确定同一目标的测量值参数组。
[1]丁鹭飞,耿富录.雷达原理[M].西安:西安电子科技大学出版社,1995.
[2]Tomas A G,Berg M C.Medadwium PRF set selection:an approach through combinatories[J].IEE Proc-Radar,Sonar Navig,1994,141(6):307-311.
[3]Trunk G,Brockett S.Range and velocity ambiguity resolution[A].The Record of 1993IEEE International Radar Conference[C],1993:146-149.
[4]雷文,龙腾,曾涛,韩月秋.一种脉冲多普勒雷达解距离模糊的新算法[J].北京理工大学学报,1999,19(3):357-360.
[5]周闰,高梅国.余差查表法单目标距离模糊的分析与仿真[J].系统工程与电子技术,2002,24(5):221-224.
