一种对MIMO雷达侦察识别的新方法
2011-06-28盛志超盛骥松
盛志超,盛骥松,杨 旋
(1.江苏科技大学,镇江212003;2.船舶重工集团公司723所,扬州225001)
0 引 言
多输入多输出(MIMO)雷达作为一种新体制雷达,通过分集技术在低截获概率、目标参数估计、动目标检测、杂波抑制、目标成像等领域的性能要优于传统雷达,引起了雷达领域众多科研工作者的广泛关注。在现代战争条件下,电子对抗面临的环境日趋激烈,以MIMO雷达为代表的新体制雷达给现代电子战提出了新的挑战,所以,急切需要研究具有针对性的侦察和对抗方法。
本文介绍了MIMO雷达的特点和常规的雷达信号分选方法,分析了它们对MIMO雷达信号进行分选的适用性,提出了一种采用奇异值分解和盲信号处理的方法对MIMO雷达进行侦察识别。
1 MIMO雷达的特点
20世纪90年代,MIMO技术在无线通信领域得到成功应用,它能够克服无线信道产生的多径衰落,改善信道的容量。由于通信系统和雷达系统的可比性,之后科研人员将其引入到雷达领域[1,2],采用多个发射和接收天线,在发射端发射的是一组正交信号,接收端每个阵元接收所有的发射信号并通过匹配滤波器组进行分选。
目前,各国的科研人员对MIMO雷达的研究主要基于2种模型,即共址MIMO雷达和分布式MIMO雷达,本文主要分析对共址MIMO雷达的侦察识别。
MIMO雷达的信号处理流程如图1所示,主要特点有:(1)抗截获性能提高,具有低截获概率(LPI)优势;(2)利用波形分集可以得到灵活的发射波束,提高检测低速目标和微弱目标的能力;(3)通过发射正交信号具有虚拟阵元的优势,产生较窄的波束和较低的旁瓣;(4)采用自适应技术获得优异的分辨力。
MIMO雷达的信号处理流程如图1所示。
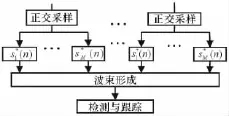
图1 MIMO雷达的信号处理流程
2 对MIMO雷达的侦察识别
2.1 常规的雷达信号分选方法
雷达信号分选是电子战信号处理的重要组成部分之一,其基本原理就是从大量混叠的脉冲信号流中分离出各个雷达脉冲序列,并选出有用信号,以此分析各个雷达的特征参数。
常规的雷达信号分选由两部分组成,即信号预分选和信号主分选。信号预分选根据瞬时参数到达角(AOA)、脉冲幅度(PA)、脉冲宽度(PD)和载频(RF)等参数来稀释脉冲信号流;接着,再利用到达时间(TOA)测量脉冲重复间隔(PRI)进行主分选。
可以发现,常规的雷达信号分选方法是按照串行规则进行检测的,无法分选同时到达的多个信号。由于MIMO雷达同时发射多个相互正交的信号,因此接收机侦收到的信号是同时到达的混合信号,如果信号设计不严格,这些信号的频域也会存在部分混叠现象。因此,常规的分选方法不能对侦收到的MIMO雷达信号进行有效的分选。
2.2 新的信号分选方法
针对常规的雷达信号分选方法无法胜任对侦收到的MIMO雷达信号的分选,本文提出了一种新的分选方法,它能够对MIMO雷达信号进行有效的侦察识别,具体包括2步:第一,采用奇异值分解对MIMO雷达所发射信号源数进行估计;第二,根据所估计的信号源数采用盲信号处理中的算法对所侦收到的混合信号进行分离处理,由所分离出信号之间的相关性判定MIMO雷达是否存在。与常规的雷达信号分选方法相比,盲信号处理技术适应复杂的信号环境,能够解决同时到达信号的分选问题。
2.2.1 对未知信号源数目的估计
在无噪声时,如果传感器数目大于信号源数目,并且信号源数据矩阵行满秩,则信号源数目等于传感器输出的混合信号数据矩阵的秩数[3]。
当存在噪声时,上述结论将不再成立。在实际
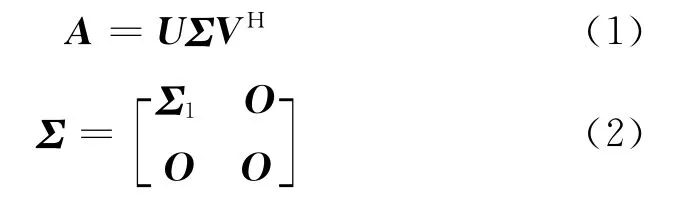
式中:Σ1=diag(σ1,σ2,…,σr),其对角元素按照顺序σ1≥σ2≥…≥σr>0,r=rank(A)排列;O为0矩阵。
设σ1≥σ2≥…≥σr>0为矩阵A的奇异值,若存在正整数ε,使得任意的i≥ε和j≤ε,总有σj≫σi,则称ε为矩阵A 的主奇异值数[4]。
在有噪声时,如果传感器数目大于信号源数目,并且信号源数据矩阵行满秩,则信号源数目等于传感器输出的混合信号数据矩阵的主奇异值数[3]。
具体的计算方法:对混合信号数据矩阵进行奇异值分解得到m个奇异值,去除最大奇异值σ1后,对剩余的按降序排列的奇异值进行如下运算:
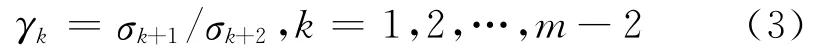
则选取ε=k+1作为矩阵的主奇异值数,选择的k满足γk= max(γ1,γ2,…,γm-2)。
另外,在有噪声时所采用的方法对无噪声的情况同样适用。
2.2.2 FastICA算法
盲信号处理包括3个主要方向:盲信号分离和提取、独立分量分析(ICA)以及多通道盲解卷积和均衡。FastICA算法[5]由荷兰赫尔辛基大学的科研人员提出,采用牛顿迭代算法,通过峭度的最大化得到伪逆矩阵W,算法的具体实现如下:
(1)对观测信号x(t)进行去均值和白化;
(2)选择初始化的随机矩阵,W = [w1,w2,…,wn]T,令p=1,g(u)=uexp(-u2/2);
(3)令k=k+1,计算y(t)=wp(k)Tx(t);
(4)根据:的信号处理过程中,噪声是不能免除的,因此,有必要考虑有噪声时对信号源数目的估计。
根据 矩 阵 的 奇 异值分解[4],对 于 矩阵A ∈Rm×n(或Cm×n),则存在正交矩阵U ∈Rm×m(或Cm×m)和V ∈Rn×n(或Cn×n)使得 :
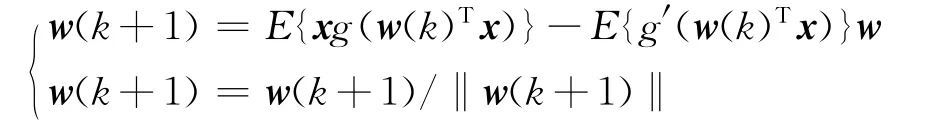
计算出 wi(k+1)。如果:‖wTi(k+1)·wi(k+1)-1‖ <ε,令p=p+1,否则转到(3),直至p=n。
(5)y=Wx得到分离信号。
3 仿真实验
MIMO雷达发射的是相互正交的信号,常见的有正交频分线性调频(OFDM-LFM)信号、正交多相编码信号和正交频率编码信号等,这里仅考虑正交频分线性调频信号。
对MIMO雷达的侦察识别是基于信号之间的相关性来判别的,首先,判断信号源数目;其次,通过盲信号分离算法估计源信号,对之做相关性处理来验证信号之间的相关性,进而可以判断是否是MIMO雷达。
为了验证前述理论,笔者做了一些仿真实验,实验参数设置为 MIMO雷达发射3个OFDM-LFM信号,频率间隔为3MHz,正交信号频率起点为10MHz,采样频率为50MHz,LFM 调频带宽为3MHz,脉冲宽度为100μs,侦察接收设备有5个阵列,混合矩阵A为一5×3随机矩阵,存在噪声时,信噪比为10dB。
3.1 仿真1,对信号源数目的估计
在无噪声时,观测信号矩阵最大的奇异值为113.928 5,将之去除后所得的4个归一化奇异值为σ2/σ2、σ3/σ2、σ4/σ2和σ5/σ2,从图2可以看出观测信号矩阵的非零奇异值有3个,而矩阵的秩数与非零奇异值个数相等,因此,在无噪声时根据观测信号矩阵的秩数就可以判断出未知信号源数目。

图2 无噪声时的奇异值
在有噪声时,观测信号矩阵最大的奇异值为113.936 0,将之去除后所得的4个归一化奇异值为σ2/σ2、σ3/σ2、σ4/σ2和σ5/σ2,从图3可以看出观测信号矩阵的非零奇异值有5个,根据2.2中的计算方法,如图4所示,最大值即为k=2处,主奇异值数ε=k+1=3,因此可以判断出未知信号源数目。
3.2 仿真2,对观测信号进行盲信号分离并作互相关处理

图3 有噪声时的奇异值
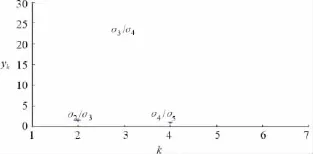
图4 比值γk
信号源数目为3,源信号波形如图5所示。在对混合信号经过FastICA算法分离后,盲信号处理结果如图6所示,可以发现盲信号处理所分离出的信号顺序与源信号顺序不是对应的,这是由于盲信号处理的不确定性所造成的。接着,对分离出的信号进行互相关处理,从图7可以看出它们满足正交性,可以基本判定MIMO雷达的存在。

图5 源信号波形
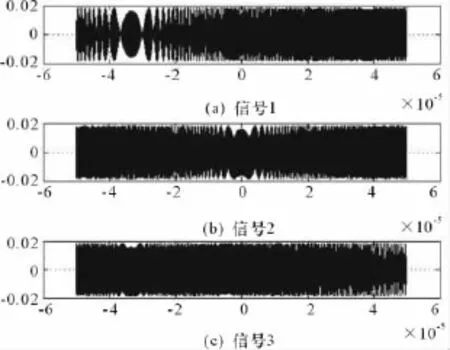
图6 盲信号处理结果

图7 信号互相关处理
4 结束语
本文将奇异值分解和盲信号处理应用到对MIMO雷达的侦察识别中,通过奇异值分解得到对MIMO雷达所发射信号源数目的估计,并且通过盲信号处理中的FastICA算法分离出MIMO雷达所发射的信号,通过互相关处理基本验证了MIMO雷达的存在。
[1]Rabideau D J,Parker P.Ubiquitous MIMO multifunction digital array radar[A].Proceedings of Signals,Systems and Computers,Conference Record of the 37th Asilomar Conference[C].Pacific Grove,CA,2003,1057-1064.
[2]Fisher E,Haimovich A,Blum R,Cimini L,Chizhik D,Valenzuela R.Spatial diversity in radars-models and detection performance[J].IEEE Transaction on Signal Processing,2006,54(3):823-838.
[3]张洪渊,贾鹏,史习智.确定盲分离中未知信号源个数的奇异值分解法[J].上海交通大学学报,2001,35(8):1155-1158.
[4]张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004.
[5]Hyvainen A,Oja E.A fast fixed-point algorithm for independent component analysis[J].Neural Computation,1997(9):1483-1492.
