迭代反馈约束下的城市轨道交通客流预测分析*

陈大伟 肖为周 李旭宏 何流

(1.东南大学交通学院，江苏南京210096;2.苏州大学城市轨道交通学院，江苏 苏州215021)

轨道交通客流预测是通过交通预测模型，在分析城市交通现状基本情况的基础上，依据城市总体规划、城市综合交通规划等上位规划，对特征年份轨道交通线路的客流规模、分布、特征进行预测，为轨道交通建设必要性、系统制式选择、建设效益分析、各项专业设计提供基础支撑，是城市轨道交通规划、设计、建设及运营各环节的基本依据，其结果可靠与否直接关系到城市轨道交通的建设投资规模、运营效率和经济效益.经过多年实践积累，我国许多城市已经逐步建立起一套完整的城市轨道交通客流预测方法和计算模型体系.吕慎等［1］采用四阶段法，利用分层次交通方式模型得到轨道交通、常规公交和接驳自行车组成的合作竞争类起讫点(OD)矩阵，采用联合方式分配模型进行轨道线网客流分析.吴祖峰等［2］采用二阶段交通方式划分模型的四阶段法，预测宁波市轨道交通线网客流.裴剑平等［3］以无锡市城市轨道交通1号线为例，应用拓展四阶段法对客流进行预测.李春艳等［4］以北京市轨道交通5号线为例，介绍了非集计基于行为的客流预测模型.由于客流预测内容和前提条件的复杂性，这些模型方法还没有达到较高的可信度.具体表现在3个方面:一是积累基础资料不足，难以掌握城市发展中的政策、经济和居民活动的变化;二是预测特征年限与作为依据的城市总体规划年限不一致，导致研究范围、城市用地与人口分布、结构形态难以稳定;三是市场经济条件下涉及诸如票制票价等因素的波动对客流的影响难以确定.文中以苏州市轨道交通2号线为例，依据城市总体规划和轨道交通沿线控制性详细规划，考虑路网机动车对地面公交出行的影响，利用分对数(Logit)公交子方式划分模型，采用迭代反馈的改进型四阶段法，探讨城市轨道交通客流预测方法.

1 模型框架

1.1 模型结构

相关研究表明:“四阶段”之间相互制约且存在循环迭代关系［5］.迭代反馈的改进型四阶段法综合考虑了社会经济、公交票价、出行时间价值、道路网络运行车速、轨道运营计划、交通发展政策等因素对出行分布及方式选择的影响，其模型结构如图1所示.该模型基于传统的四阶段法，道路网络机动车车流模型与交通分布、方式划分模型相互作用，循环迭代，达到平衡收敛.初始交通分配结果预加载到道路网络，用于出行成本计算，据此对出行分布、方式划分进行调整，并产生新的交通分配结果.

图1 轨道交通客流预测模型结构Fig.1 Structure of the forecast model for rail transit passenger flow

1.2 模型原理

1.2.1 交通生成模型

交通生成包括出行产生和出行吸引，前者以出行者的社会经济特征为主，与其出行强度关系最大，后者以土地利用的布局为要，与土地利用的性质、开发强度相关［6］.模型在小区人口、用地规模以及开发强度预测的基础上，按照出行发生和吸引率预测小区的出行产生和吸引.

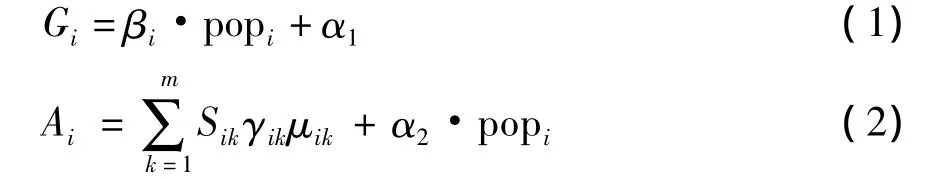
式中:Gi、Ai分别为交通小区i的产生量和吸引量;popi为该小区预测人口数;βi为该小区平均出行强度;Sik、γik、μik分别为 i小区第 k 类用地的面积、开发强度、单位建筑面积的出行吸引率;α1和α2为偏回归系数.

1.2.2 交通分布模型

交通分布采用双约束重力模型:

1.2.3 方式划分模型

从目前国内城市交通预测的实践来看，在进行居民出行方式划分的预测中，普遍的趋势是:宏观控制与微观预测相结合，宏观指导微观［7］.在宏观控制上，充分体现城市交通发展战略目标的控制作用，依据国家未来经济政策、交通政策对未来城市交通结构做出估计.在微观预测中，则根据城市各种交通方式的特征并考虑到轨道交通与其他交通方式的合作竞争关系，应用Logit交通方式划分模型预测各特征年包含轨道交通的公交交通方式分布矩阵，再利用居民SP调查建立的Logit公交子方式划分模型，预测轨道交通方式分布矩阵.

(1)步行交通方式.

步行出行方式主要受出行距离的影响，预测采用步行拟合曲线函数法.由居民出行调查资料可以获得出行者分距离各方式的出行次数，选取特定距离下各类交通方式出行数占此距离总出行数的出行比例，可以得到步行交通方式分担率曲线.

(2)自行车、电动自行车、小汽车、公交车出行方式.

自行车、电动自行车、小汽车、公交车之间存在竞争关系，考虑车内出行时间、等车时间和步行时间，同时考虑到不同方式间存在的IIA(Independent and Irrelevant Alternatives)问题，这里采用树状分对数(Nested-Logit)模型进行计算.

其中:

式(4)－(10)中:Pijn为 i和 j同时选择概率，Pj/in、Vj/in分别是在上层选择i的条件下，在下层选择j的条件概率和效用，Pin、Vin分别是在上层选择i的概率和效用;Vbike、Vebike、Vcar、Vbus分别为自行车、电动自行车、小汽车、公交车的出行效用;tvt为公交车的车内时间或自行车、电动自行车、小汽车的出行时间;twait和twalk分别为公交车出行的等车时间和步行到站时间;λ1、λ2、θ1－θ6为待定参数.

(3)轨道交通出行方式.

由居民SP出行调查信息，利用轨道交通和地面常规公交两种交通方式出行效用差，考虑步行到站时间、步行出站时间、等车时间、车内时间、换乘惩罚时间、换乘次数的影响，建立Logit公交子方式划分模型，预测轨道交通出行矩阵.

式(11)中:

式中:M1表示步行至轨道交通站、出站后步行达到目的地，出行过程中没有使用常规公交;M2为出行过程中通过常规公交换乘轨道交通;B1表示出行过程中没有使用轨道交通，仅使用一次常规公交;B2表示出行过程中没有使用轨道交通，但使用两次或者两次以上常规公交.

Pmetro为轨道交通出行概率;U为出行效用差;tgc为车内广义时间;tgo为车外广义时间;tM1gc为M1模式下的车内广义时间(其余类似);tvt为车内时间;FARE为票价;VOT为时间价值;tiw为初始等车时间;ttw为换乘等车时间;tt为换乘时间;ta为步行至车站的时间;te为出站后步行时间;MT为轨道交通出行换乘次数;BT为公交出行换乘次数;a～g为变量系数.

1.2.4 交通分配模型

交通分配模型包括道路网络机动车交通分配模型和公交网络轨道交通客流分配模型［8］.道路网络机动车交通分配采用用户平衡模型，公交网络轨道交通客流分配采用最短路径法，分配过程中的阻抗为广义出行费用.

1.3 收敛判定及迭代方法

根据交通分配模型得到的道路交通流量，对路段通行时间进行更新，进而改变交通分布模型中各OD对之间的最小效用d'ij，并以此重新计算交通分布T'ij=aiGibjAjf(d'ij).根据两次OD矩阵的相似程度，判断是否收敛［9］.收敛判断采用总方差根法(RSE)，计算公式如下:

式中:ε为用户设置的反馈收敛精度目标.当ε不满足式(13)时，需要对OD结果进行修正，这里采用连续平均法(MSA)［10］.将前后两次出行分布的结果进行加权平均，权重随迭代次数的增加而减小.

2 模型构建

2.1 基础数据

(1)居民出行调查数据.

主要包括居民家庭属性、个人属性以及个人出行特征.

(2)交通量调查数据.

主要包括路段和核查线交通量调查数据.路段交通量调查数据主要为路段不同出行时段各类车辆数量;核查线交通量调查数据主要为关键控制点不同出行时段各类车辆数量和人行流量.

(3)人口、用地、就业岗位分布数据.

将研究范围划分为轨道沿线地区、中心城区非轨道沿线地区和外围地区非轨道沿线地区.轨道交通沿线地区采用城市控制性详细规划，而非沿线地区采用城市总体规划进行研究范围内人口和就业岗位的总量控制，即通过协调城市用地建设的总体开发强度和局部地区的开发强度，从而保证城市用地总体开发强度的平衡.

(4)道路网络信息.

主要包括道路路段基本属性、容量、行车时间、步行时间、运营车速等.

(5)公交运营线路信息.

包括地面常规公交和轨道交通线路基本信息，主要为高峰发车间隔、平峰发车间隔、票制票价等.参考国内城市轨道交通票制票价设置情况，苏州轨道交通票制采用里程制，起步价为2元，全程为6元，表1为苏州轨道交通票价方案.

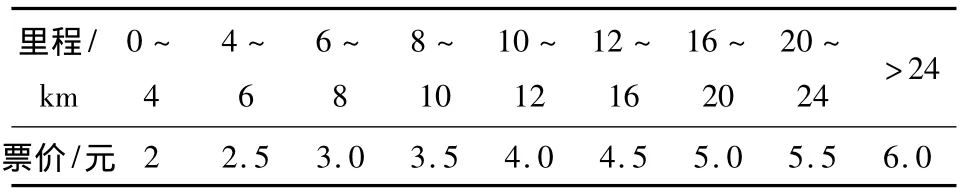
表1 轨道交通票价方案Table 1 Price scenarios of rail transit

2.2 网络构建

基础网络由物理网络和网络参数构成.物理网络包括道路网络、地面常规公交网络和轨道交通网络.地面常规公交和轨道交通网络均建立在道路网络之上.地面常规公交网络包括公交路段和车站两部分，出行者步行到达车站乘坐公共交通，其运行时间参数从道路网络上获取.轨道交通网络运行时间参数由轨道运营计划获取.

3 模型应用

3.1 苏州轨道交通2号线概况

苏州轨道交通2号线全长26.4 km，共设车站22座，其中换乘站4座，一般站18座，平均站间距为1.26km，计划2013年建成通车.该线路是苏州市计划实施的第2条轨道交通线路，起于相城区京沪客运专线新苏州站，由北至南沿古城区西外城河纵贯市区，止于吴中区迎春南路，途经苏州火车站、石路商业中心、宝带路地区，将相城区中心、中心分区、吴中区中心联系起来，属于交通疏导兼城市引导型线路，紧密联系了城市南北两端的城镇，有利于促进城市发展轴的快速构建.

客流预测研究范围为苏州市区，目前城市总人口424万人，总建筑面积36134万m2.根据城市总体规划，2020年城市总人口为500万人，总建筑面积为42067万m2.2号线两侧沿线800m范围内，目前总人口74.9万人，总建筑面积3085万m2.根据轨道交通沿线控制性详细规划，2020年苏州轨道交通2号线沿线地区总人口92.1万人，总建筑面积4885万m2.

3.2 应用结果

(1)模型迭代效果.

根据上述模型结构和原理，采用迭代反馈的方法对苏州轨道交通2号线客流进行预测.图2为采用迭代客流预测模型在不同目标年的迭代效果.结果显示，若取ε=5%，3个目标年迭代次数分别为7、9和10次时，预测模型即收敛.同时随着预测年份越远，收敛迭代次数越多.

图2 迭代效果图Fig.2 Iterative diagram

(2)线路客流量.

预测轨道交通2号线初期、近期、远期日均客运量分别为25.82、43.03和66.72万人次，高峰小时单向最大断面客流量分别为1.19、1.81和2.53万人次.表2为轨道2号线各特征年客流指标预测值.从客运量增长趋势看，轨道2号线开通10年内，客运量年增长7.6%，之后15年，年均增长3.0%，客流增长趋势符合一般增长规律［11］.

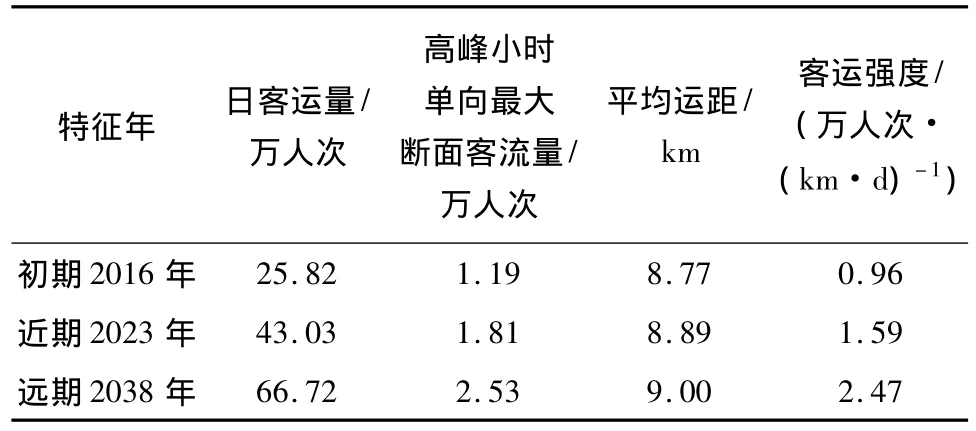
表2 轨道线路特征年客流指标预测值Table 2 Predictive value of rail transit passenger flow for target years

4 结论

文中采用迭代反馈模型对城市轨道交通客流进行预测分析和研究，在数据处理、模型构建和模型应用等方面有一定的进展.

(1)保持研究范围基础数据的协调性.突破传统研究范围内基础数据难以把握的特点，根据区位特征提出将研究范围划分为轨道沿线地区、中心城区非轨道沿线地区和外围地区非轨道沿线地区.轨道交通沿线地区采用城市控制性详细规划，而非沿线地区采用城市总体规划，通过协调总体与局部的开发强度，从而保证城市人口和就业岗位的重新平衡.

(2)对传统四阶段模型进行了改进.通过考虑机动车车流对公交车运行的影响，使机动车车流分配模型与交通分布、方式划分模型相互作用，迭代反馈，达到平衡收敛.道路路段货车车流对公交车运行也会产生一定的影响，这方面的研究有待深化.

(3)以苏州市城市轨道交通2号线为例，采用迭代反馈模型对其进行了客流预测和分析，迭代结果表明，在3个预测目标年，当分别迭代至7、9和10次时，预测结果即达到精度要求，符合收敛条件;从客流指标预测结果来看，客流增长趋势也符合一般客流增长规律.

［1］吕慎，过秀成.轨道线网客流预测方法研究［J］.系统工程理论与实践，2001(8):106-110.Lü Shen，Guo Xiu-cheng.Method of the URT’s passenger flow forecast［J］.Systems Engineering Theory ＆ Practice，2001(8):106-110.

［2］吴祖峰，沈菲君.轨道交通客流预测方法研究［J］.宁波高等专科学校学报，2004，16(4):24-28.Wu Zu-feng，Shen Fei-jun.Method of estimate passenger flow of URT ［J］.Journal of Ningbo College，2004，16(4):24-28.

［3］裴剑平，范东涛.基于拓展四阶段法的城市轨道交通客流预测［J］.都市快轨交通，2010，23(5):57-61.Pei Jian-ping，Fan Dong-tao.Passenger flow forecast for urban rail transit based on extended four step model［J］.Urban Rapid Rail Transit，2010，23(5):57-61.

［4］李春艳，陈金川，郭继孚，等.基于行为的客流预测方法探讨及应用［J］.交通运输系统工程与信息，2006，6(6):143-148.Li Chun-yuan，Chen Jin-chuang，Guo Ji-fu，et al.Research of activity-based passenger forecast used in Beijing metro line 5 ［J］.Journal of Transportation Systems Engineering and Information Technology，2006，6(6):143-148.

［5］全永燊.城市交通客流预测的若干问题［J］.城市交通，2008，6(6):5-8.Quan Yong-shen.Comments on issues regarding urban travel forecasting ［J］.Urban Transport of China，2008，6(6):5-8.

［6］张晓明.城市交通出行生成模型的研究［D］.北京:北京工业大学交通学院，2000.

［7］李旭宏.道路交通规划［M］.南京:东南大学出版社，1997.

［8］过秀成，吕慎.基于合作竞争类OD联合方式划分轨道客流分配模型研究［J］.中国公路学报，2000，13(4):91-94 Guo Xiu-cheng，Lü Sheng.Study of URT’s joint modal split assignment model on cooperative and competitive OD matrix［J］.China Journal of Highway and Transport，2000，13(4):91-94.

［9］曲云超，徐猛.求解交通出行预测的反馈四阶段法研究［J］.中国科技论文在线，2008，3(10):725-730.Qu Yu-chao，Xu Meng.Study on four step procedure with feedback solving travel forecasting problems［J］.Sciencepaper Online，2008，3(10):725-730.

［10］陈大伟，徐中，李旭宏.高速公路网互通立交布局优化模型 ［J］.交通运输工程学报，2010，10(3):72-77.Chen Da-wei，Xu Zhong，Li Xu-hong.Layout optimizing model of alternative interchange in highway network［J］.Journal of Traffic and Transportation Engineering，2010，10(3):72-77.

［11］叶霞飞，明瑞利，李忍相.东京、首尔轨道交通客流成长规律与特征分析［J］.城市交通，2008，6(6):16-20.Ye Xia-fei，Ming Rui-li，Li Ren-xiang.Rail Transit in Tokyo and Seoul:development trends＆characteristics of passenger flow ［J］.Urban Transport of China，2008，6(6):16-20.