复杂系统中基于场与结构耦合效应的一些涌现特性及其物理机制

黄吉平

(复旦大学物理系,上海 200433)

复杂系统中基于场与结构耦合效应的一些涌现特性及其物理机制

黄吉平

(复旦大学物理系,上海 200433)

复杂系统涌现性的场与结构的耦合效应是一个非常值得关注的研究课题,这是因为该耦合效应能够描述各种复杂系统具有的一个共性,即这些系统都包含两类基本相互作用.一类是个体之间的相互作用(它确定了系统的初始“结构”);另一类是个体与环境(该“环境”给定了系统所处的外“场”)之间的相互作用(该相互作用通过与系统内部的相互作用耦合,确定了系统的最终“结构”).本文综述了一些复杂系统的涌现特性,主要介绍了其中的场与结构的耦合效应的研究进展.这些特性的介绍不仅有助于特定系统自身的发展和应用,而且有助于为发展描述各种复杂系统的普适理论奠基.

涌现性;复杂性;统计物理

1 复杂系统及复杂性概述

自20世纪90年代Holland[1]提出复杂适应系统理论起,复杂性科学的研究蓬勃兴起,至今方兴未艾[2-25].复杂性科学是描述复杂系统的复杂性的科学.复杂系统从研究对象上看,它可以包含的范围很广,小到基本粒子、胶体颗粒,大到经济市场、人类社会……甚至宇宙.但是,尽管如此,这些系统必需具有复杂性,方才是名副其实的“复杂系统”,否则,就是简单系统或随机系统——这两种系统运用牛顿力学或简单的统计平均(基本)就能分别解决了.例如:“复杂流体”和“经济物理”的研究领域都可以视为“复杂系统”的研究范畴,这是因为“复杂流体”具有复杂性,“经济物理”的主要研究对象是经济市场,这个研究对象正以其复杂性而让“无数英雄竞折腰”.虽然自20世纪90年代起,复杂系统的研究才白热化起来,但是,随着研究的不断深入,复杂系统的范畴被逐渐扩大了,人们把之前广泛研究过的“分形”等系统也都囊括其中——这是因为,随着研究的深入,学者们发现这些“古老的”系统也具有“复杂性”.

至此可见,复杂性是复杂系统的基本特性,主要指复杂系统的学习性、适应性和涌现性.学习性和适应性是指系统主体(agent,或译为“行为人”)的属性,其中“学习性”指主体具有学习和纠错的能力,而“适应性”与“学习性”是相辅相成的,它表示主体具有适应外界环境(和众多其它主体)的能力,“适应性”可以视为单个主体“学习”的目的,而“学习”就是主体实现“适应性”的过程.“涌现性”是指系统整体性质大于部分之和,或整体具有单个个体所不具有的性质.涌现本身具有层次性,底层的主体涌现出高层的性质,高层的性质可以涌现出更高层的性质,依次类推.鉴于涌现性的重要性,研究复杂系统的“复杂性科学”就是研究复杂系统的“涌现性科学”.因为,学习性和适应性可以看做是实现涌现性的过程,而涌现性则是学习性和适应性的演化结果.从“涌现性”的角度看,化学是物理学的涌现结果,而生物学则是化学的涌现结果,社会学则是生物学的涌现结果……这也从一个侧面说明,复杂系统的研究是一个交叉学科.或许,原本的学科划分就是源于学者们的孤陋寡闻,因为当今世界没有几个人能够精通数个学科,所以只能在特定的学科中摸爬滚打.

复杂系统的涌现性主要源于(低层次上)个体之间及个体与环境之间的非线性相互作用,这种相互作用是主动的、反复的.正是这种相互作用的存在导致该系统趋向混沌的边缘,即成为介于有序与无序之间的具有涌现性的特殊区间.

目前尚无适用于复杂系统的普适理论[1],或说,人们迄今尚未发现描述复杂系统中非线性相互作用机制的一般理论.也许,这不是学者们无能,而是复杂系统本身的复杂性(或狭义地讲——涌现性)导致一般的普适理论客观上并不存在.例如,这些系统因与环境有交互作用而边界模糊(或没有边界)也算一个可能的客观原因.这里有必要提及的是,对于耗散系统(复杂系统中的一个亚类)而言,耗散结构理论却是一个非常成功的理论.

2 复杂系统的方法论

处理复杂系统的具体方法不一而足,对不同系统,方法迥异,但总的来说,这些方法可以简单地分为两类:一类是自下而上的“涌现”方法,另一类是自上而下的“控制”方法.但是,不论哪一类,从方法论角度看,复杂系统中比较常用的是“整体论”,这与处理一些简单系统的“还原论”不同.“整体论”主要用的是“归纳法”,而“还原论”主要用的却是“逻辑演绎”.当今科学界,特别是物理领域,仍旧是“还原论”大行其道的年代,希望“整体论”的引入能够解决“还原论”还没有解决的硬骨头,例如神经网络、生命的起源、经济危机等.因为“还原论”的成功使用,所以物理学家们认为“世界是简单的”；因为“整体论”的引入,所以复杂系统领域的专家们认为“世界是复杂的”.作为一般读者,不必混淆,这并不矛盾,“世界是简单的”的论断基于“整体=部分之和”的“简单性”而言,而“世界是复杂的”仅仅是基于“整体不等于部分之和”的“复杂性”而言的.这里“简单”和“复杂”,仅仅是相对的、而非绝对的,它们可以视为是人们在认识自然或社会时的两个不同的侧面而已.例如,西医是以还原论来治病救人的,所以,在西医眼中,人的一些脏器是可以切除的,因为他们认为“人”是“简单的”——“人”的各个部分之和等于“人”这个整体；而中医则是以整体论来治病救人的,所以,在中医眼中,人的脏器是断断不可切除的,因为他们认为“人”是“复杂的”——“人”的各个部分之和不等于“人”这个整体.从这里也可以看出,所谓中西医之争似乎就是两种方法论之争.

3 研究复杂系统的一个重要手段:基于多主体的模拟研究

对“涌现性”的研究是研究复杂系统的核心问题,既有的基于多主体(multi-agent-based)的研究绝大多数都是基于计算机模拟来实现的.对于初学者而言,这里有兴趣推荐一些比较好的基于主体模拟的模型平台,从而有助快速入门,以便可以把时间花在课题本身的研究内容上,而不必花在计算机编程

这类的技术活上,这些平台有:SWARM,REPAST, ASCAPE和TNG Lab.这些平台都是基于多主体模拟设计的,它们已经取得很大的成功.但是,人们用基于多主体模拟的手段来研究复杂系统,仍旧用的

是隐喻的方法论思想,他们把研究对象(复杂系统)本身,在不同的层次上划分为不同的主体,从而抽取其中一些主要的特性,赋予主体,再设计模拟方法(建模),并进行运行.显然,这样的模拟是对原系统的一种隐喻式的研究,这样的研究暂时摒弃了一些不必要的因素,可以有助于挖掘导致“涌现性”的主要因素.

4 描述复杂系统的模型

从研究复杂系统的模型角度出发,除了在特定学科中原有的模型(例如物理学、化学、生物学、生态学等中与复杂系统有关的已有的模型或方法)外,目前广泛使用的、新发展的模型有:元胞自动机(cellular automation)模型、网络模型、受限生成系统模型、博弈模型、统计分析模型等[2-20].“元胞自动机模型”就是一个描述在规则格点上的元胞随着时间和空间演化的动力学系统.网络模型,就是把主体之间的关系视为网络的一种研究模型,相关网络主要有无标度网络、随机网络等,在此领域,国内学者的成果非常显赫[2-16].至于受限生成系统模型,主体在与其它主体或环境发生交互作用时,既有正反馈也有负反馈,负反馈可以导致主体的消亡或衰减,而正反馈能够导致主体的适应(生存),受限生成系统模型就是对各种反馈进行内生的、非外部强加的限制,从而使主体更好的适应其它主体和环境.至于博弈模型,也比较容易理解,经济物理学研究中常用的少数者博弈(minority game)模型就属此类,少数者博弈模型及其衍生版本的主要目的就是研究如何合理分配有限资源,这也正是传统经济学研究的核心课题.值得一提的是,当前在博弈模型领域的经济物理研究,已经有一些可控的真人实验的研究工作[21-22],这些工作的出现标志着对于经济市场复杂系统的研究已经不再局限于单纯的理论探索或基于经验数据的统计分析,而是可以以“主体或行为人”为研究对象,开展真正意义上对真人的可控实验研究.所谓统计分析模型就是指以复杂系统产生的海量数据为研究对象,利用统计(物理)学的手段分析数据的关联、分布(等等)的方法,此方法有助揭示该类复杂系统的相关统计规律(涌现性之一种),例如,幂律分布等.

5 复杂系统研究的一个前沿领域简介

复杂系统中场与结构耦合诱导的涌现特性研究正如前文所述,复杂系统的“复杂性”通常体现在系统宏观性质与微观性质的不同,或说,部分加部分的简单叠加不等于整体.可是,复杂系统的“涌现特性”则是指系统高层次的性质是由低层次的性质决定的.显然,该“涌现特性”与“复杂性”有关联,也有区别.一个系统是否能够被称为“复杂系统”,主要就看它是否具有“复杂性”,至于“涌现特性”,它通常伴随“复杂性”而存在(主要源于系统内部的非线性动力学机制).正如上文所提及的,从研究对象来看,复杂系统可以包含的系统很广,有自然系统,亦有社会系统,原则上,只要这些系统具有上述的“复杂性”,这些系统也就可以视为复杂系统了.例如:

a.胶体悬浮液——微观上,悬浮颗粒自身具有三次光学非线性响应,而宏观上,该胶体悬浮液系统具有源于局域场增强的有效三次光学非线性响应,这个“有效三次光学非线性响应”非微观颗粒自身的“三次光学非线性响应”简单叠加所能获得,所以,这里就体现了胶体悬浮液的一种复杂性.

b.经济市场——微观上,每个行为人的决策都是自利的,但是,宏观上却(可以)导致一种利他的(有序)结果,这里的利他结果同样非单个行为人的“自利行为”简单叠加所能够获得的,所以,这里也体现了经济市场的一种复杂性.

当前复杂性科学研究的一个前沿领域是复杂系统中场与结构耦合诱导的涌现特性研究,仍以上述例子说明:

a.胶体悬浮液中光波的电场分量,其强度和分布,可以由胶体颗粒们不同的微结构来给定,同时亦可反过来调节胶体颗粒们的微结构,这就导致了体系内不同强度或分布的局域场增强效应,该效应直接导致该系统具有增强的有效三次非线性光学响应,这是场-结构耦合诱导的涌现特性之一.

b.对经济市场而言,单个行为人做自利的决策时,通常都是对所能获得的外界信息响应的结果,这个响应可以视为一种“场”.在不同场的影响下,不同的行为人作出了不同的决策,这可以使得整个市场中行为人的结构(例如:买卖人数比、交易量等)发生改变,而结构改变的同时,行为人所受的“场”也相应变化了,最终,整个市场好像有只“看不见的手”在起着调节作用,这是场-结构耦合诱导的涌现特性之二.

据此,可以清楚地看到,尽管在看似迥异的复杂系统中(如:胶体悬浮液与经济市场),场与结构耦合诱导的涌现现象皆可出现.只是,此时的“场”既可以是传统物理学中的电场、磁场等,也可以是一种由多种因素产生的外力合成而生的“等效场”,例如:经济市场中各种信息流合成的“等效场”.从这两种在传统观念中似乎很不一样的体系的分析过程中也可以看出,复杂系统的研究内容确实非常广泛.但是,当我们把这些广泛的研究对象都合理地归于“复杂系统”的这个大旗之下时,将有助于启发人们寻找描述复杂系统的普适理论[1].其实,“复杂流体”(如胶体悬浮液)一直就是“复杂系统”的一个分支,只是因为其自身源于非凡的应用需求而发展迅猛,所以,常常单立开去,无疑,此举对寻找复杂系统的普适理论不是很有利.

总之,“涌现特性”是复杂系统的一个重要性质,一般而言,研究涌现特性的方法非常复杂.但是,基于场与结构耦合效应的探索,有望为复杂系统的涌现特性研究开辟一条比较明朗的大道.

6 复杂系统中场与结构耦合诱导的涌现特性研究成果简介

在此,将介绍本课题组取得的4项成果,即:

a.揭示了经济市场复杂系统中外场(即外部信息)与市场结构的耦合诱导的涌现结果——“看不见的手”[21]；

b.揭示了经济市场复杂系统中外场(即外部信息)与市场结构的耦合诱导的涌现结果——宏观资源分配中的有益跟风[22]；

c.揭示了铁磁流体复杂系统中外场与系统结构耦合诱导的涌现结果——光学负折射现象[23]；

d.系统研究了颗粒复合材料复杂系统中光场与材料结构耦合诱导的涌现结果——增强非线性光学响应[24-25].

这些研究成果可以有两层意义:一是把这类场-结构耦合涌现机制应用到特定的复杂系统中获得特定的、有用的涌现结果,推动了特定系统所在特定领域的研究进展；二是通过研究尽可能多的特定的复杂系统,可以把这类场与结构耦合涌现机制推广到尽可能多的复杂系统,从而为寻找描述复杂系统中非线性相互作用机制的一般理论奠基.下面逐一介绍。

6.1 揭示了经济市场复杂系统中外场(即外部信息)与市场结构的耦合诱导的涌现结果——“看不见的手”[21］

“看不见的手”是经济市场复杂系统中的一个涌现结果,这是因为市场整体所呈现出的这个性质并非单个行为人所具有,而是主要通过市场微结构与外场(如:各种外部信息)的非线性耦合而涌现出来的,这是从一般复杂系统的角度说的.下面将从本课题组的研究对经济市场所在的这一特定领域(即“复杂适应性系统”)的意义进一步进行阐述.

230多年前,亚当·斯密在《国富论》中指出:自由市场表面看似混乱而毫无拘束,实际上却是由一双所谓的“看不见的手”(invisible hand)所指引,引导市场生产出正确的产品数量和种类.这只“看不见的手”不仅存在于经济市场中,也广泛存在于各种社会或生物系统中.这些由大量相互作用的个体组成的“复杂适应性”系统,对环境具有高度的适应能力.系统内的个体以自利为原则决策各自的行为,在对系统内分布不均的有限资源的竞争中导致系统整体上有效的(合理的、均衡的)或非有效的资源配置.实际生活中的资源分配现象往往面临资源的非均匀分布.通常认为,在普遍存在的“看不见的手”的引导下,系统资源的配置最终可以达到一种理想的均衡状态,即有效配置状态.然而,现实当中这种所谓“看不见的手”有时也会失效,即所谓的“市场失灵”现象.

传统经济学通常关注于上述现象的应用,而对其背后的微观动力学机制所涉不多.该项研究聚焦于非均匀分布的资源分配问题,通过开展一系列真人实验发现:即使完全没有实验参加者之间的直接交涉,也完全没有外部力量对参加者进行的协调,实验中的虚拟资源的配置还是达到了有效状态(见图1).然后,在“少数者博弈”(minority game)模型的基础上构建了“市场导向的资源分配博弈”(marketdirected resource allocation game,MDRAG)模型.新模型很好地解释了实验结果.与此同时,通过MDRAG模拟,提出了“看不见的手”作用的一种可能的微观机制,并且发现了使其发挥调节功效的充分条件:第一,资源竞争的参与者所持的竞争战略必须具备足够的多样性,对分布于各处的资源的偏好能随环境演化而自动调整；第二,市场参与者的决策能力必须与环境的复杂程度相匹配.更为有趣的是, 在MDRAG的模拟结果中存在多个相变过程[21],而正是在这些相变的临界点附近,“看不见的手”的调节功效可以被发挥到极致,此时的资源分配市场呈现出配置有效、波动稳定、波动方向不可预测的状态.

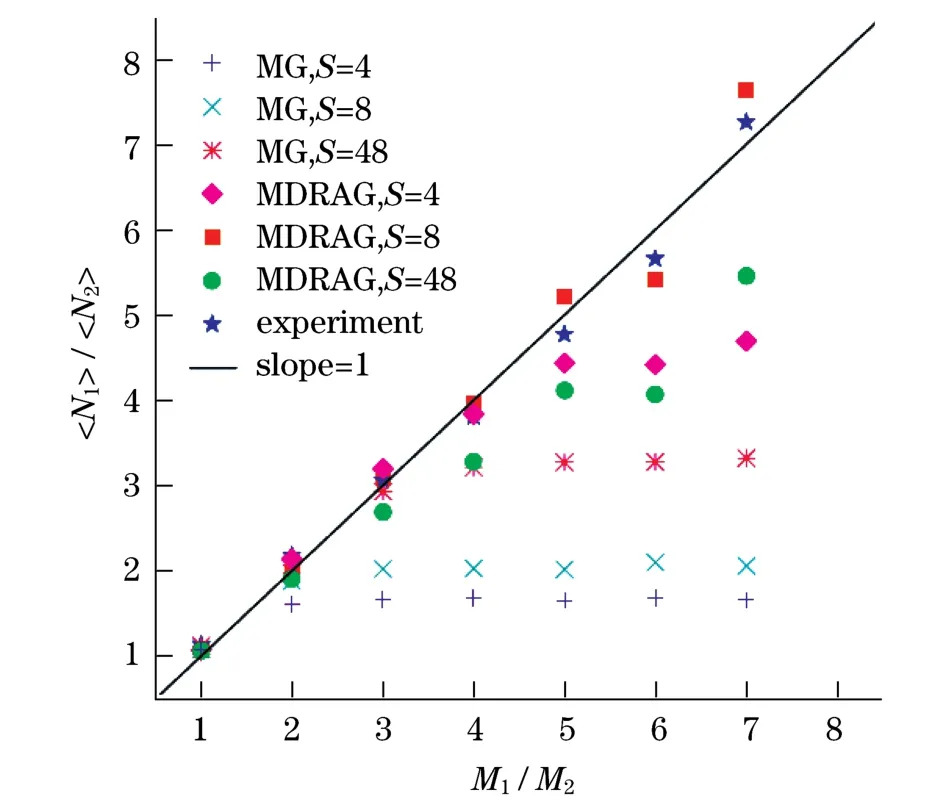
图1 真人经济物理实验结果及基于市场导向资源分配博弈模型(MDRAG)的计算机模拟结果图[21］Fig.1 Experimental results of human econophysics experiments and computer simulation results based on the Market-Directed Resource-Allocation Game(MDRAG)[21］

6.2 揭示了经济市场复杂系统中外场(即外部信息)与市场结构的耦合诱导的涌现结果——宏观资源分配中的有益跟风[22］

跟风是经济(金融)市场中司空见惯的现象,已有不少学者就跟风的理性与非理性进行了深入的研究.研究结果发现,跟风在某些情况下是理性的——例如当行为人在对环境不了解的情况下选择的“跟风”；但是,跟风在某些情况下却是非理性的——例如当行为人有自己的决策但却选择了放弃而盲目“跟风”.这些研究都是从行为人这个微观个体层面上来进行分析的.当涉及到宏观层面时,普通的看法是,跟风会导致市场中的波动加剧,从而可能导致市场崩溃,这也正是人们一直把跟风看作是导致经济危机出现的罪魁祸首的重要原因.

但是,通过一系列真人经济物理实验和基于行为人的计算机模拟研究发现,就市场的宏观资源分配效率而言,跟风在某些情况下却起着非常积极的意义(见图2).进一步的理论分析表明,统计物理中的相变理论有助于界定有益跟风与有害跟风.此项研究对经济学、社会学、生态学以及物理学等皆有一定的意义.

6.3 揭示了铁磁流体复杂系统中外场与系统结构耦合诱导的涌现结果——光学负折射现象[23］

光学负折射现象是基于铁磁流体复杂系统的一个涌现结果,这是因为系统整体所呈现出的这个性质并非单个个体(例如其中悬浮的纳米铁磁颗粒)所具有的,而是主要通过系统微结构与外场的非线性耦合涌现出来的,这是从复杂系统的角度说的.下面再从该成果对该系统所在特定领域的意义进行阐述.

本课题组运用有限元数值模拟方法在外加直流磁场作用下的铁磁流体中揭示了全角宽频光学负折射现象(见图3).该铁磁流体是由四氧化三铁颗粒外面包裹银壳层分散在水中形成.在不加外磁场的情况下,复合颗粒均匀分散在水中.在外加直流磁场的情况下,颗粒会聚集成链或柱状结构,链/柱的长短依赖于外磁场的大小,换言之,外加磁场可以用来调节系统内部的微结构.其中揭示的可调的全角宽频光学负折射来源于磁场诱导的链/柱状结构(即磁场感应各向异性微结构)与光场的耦合.

6.4 系统研究了颗粒复合材料复杂系统中光场与材料结构耦合诱导的涌现结果——增强非线性光学响应[24-25］

增强非线性光学响应是基于颗粒复合材料复杂系统的一个涌现结果,这是因为系统整体所呈现出的这个性质并非单个个体(例如颗粒)所具有,而是主要通过系统微结构与光场的非线性耦合而涌现出来,这是从复杂系统的角度说的.下面将进一步阐述其在特定领域的研究意义.

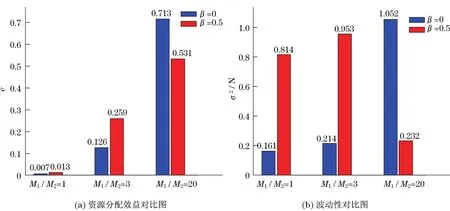
图2 真人经济物理实验结果图[22］Fig.2 Experimental results of human econophysics experiments[22］

图3 铁磁流体的光学负折射现象的有限元模拟结果[23］Fig.3 Optical negative refraction of ferrofluids: Results of the finite element method[23］

具有增强非线性光学响应的光学材料(也叫增强非线性光学材料)在许多方面有着重要的应用,例如可以用于光学开关等.一般说来,只要能够获得这类高性能的光学材料,已经经过实验论证的非线性光学的许多应用都可以变为现实.

复合材料通常是由两种或多种材料复合而成,这类材料往往具有单个组元材料不具备的物理性质(涌现性).非线性光学复合材料是指由两种或多种非线性光学材料(其中至少一种组元材料具有非线性光学响应)复合而成的材料,这类材料的非线性光学响应因为可以比单个组元材料的更强,而拥有比较广阔的用途.我们基于复杂流体的场感应各向异性的特性,设计并研究了一类新颖的软物质非线性光学复合材料.这里提及的“软物质非线性光学复合材料”由两种或两种以上的组元材料复合而成,其中至少有一种组元材料是液态的,并且这类复合材料的微结构在外场(例如电场、磁场、光场等)作用下可实时调节(见图4).这类因结构可调而性质变得可调的材料能够具有更为丰富的非线性光学响应.

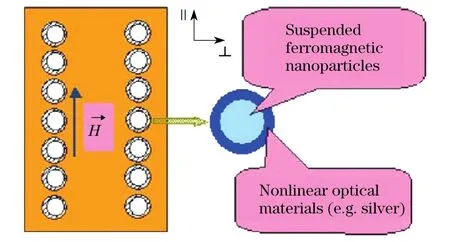
图4 具有增强非线性光学响应的软非线性光学材料设计[24］Fig.4 Design of soft nonlinear optical materials with enhanced nonlinearity[24］

7 结语与展望

复杂系统涌现性的研究是个极富挑战性的研究领域,该挑战性主要体现在系统种类的多样性(近乎无穷),以及已有理论和实验的局限性与片面性.研究涌现性的场与结构的耦合效应应该是一个值得关注的切入口,这是因为该耦合效应能够描述各种复杂系统都具有的一个共性,即它们都包含两类基本相互作用,一类是个体之间的相互作用(它确定了系统的初始“结构”),另一类是个体与环境(该“环境”正给定了系统所处的外“场”)之间的相互作用(该相互作用通过与系统内部的相互作用耦合,确定了系统的最终“结构”).已有的研究表明这些工作对特定的系统有一定的价值,推而广之,它们亦有助于建立描述复杂系统涌现性的普适理论,可是,现在离这个梦想的实现还非常遥远.

[1] HOLLAND J H.Can There be a Unified Theory of Complex Adaptive Systems[M].New Jersey:Addison-Wesley,1995.

[2] 方锦清.驾驭强流束晕与探索网络科学[M].北京:原子能出版社,2008.

[3] 何大韧,刘宗华,汪秉宏.复杂系统与复杂网络[M].北京:高等教育出版社,2009.

[4] 汪秉宏,王文旭,许伯铭.复杂网络[M].上海:上海科技教育出版社,2006.

[5] 汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社,2006.

[6] 王林,戴冠中.复杂网络的Scale-free性、Scale-free现象及其控制[M].北京:科学出版社,2009.

[7] 史定华.网络度分布理论[M].北京:高等教育出版社,2011.

[8] YANG H,NIE Y,ZENG A,et al.Scaling properties in spatial networks and their effects on topology and traffic dynamics[J].Europhysics Letters,2010,89 (5):58002

[9] XIA Q Z,LIAO X H,LI W,et al.Enhance cooperation by catastrophic collapses of rich cooperators in coevolutionary networks[J].Europhysics Letters,2010,92 (4):40009.

[10] ZHANGJ B,LIU Z R,XU J H.Synchronization in oscillator networks with coupling balance[J].Chaos, Solitons&Fractals,2009,39(2):556-566.

[11] ZHONG L X,ZHENG D F,ZHENG B,et al.Networking effects on cooperation in evolutionary snowdrift game[J]. Europhysics Letters,2006,76(4):724-730.

[12] XIONG D X,ZHAO H.Estimates of storage capacity in the q-state Potts-glass neural network[J].Journal of Physics A:Mathematical and Theoretical,2010,43 (44):445001.

[13] QIU T,ZHENG B,CHEN G.Financial networks with static and dynamic thresholds[J].New Journal of Physics,2010,12(4):043057.

[14] YEUNG C H,WONG K Y M.Self-organization of balanced nodes in random networks with transportation bandwidths[J].The European Physical Journal B, 2010,74(2):227-233.

[15] GU C G,ZOU SR,XU X L,et al.Onset of cooperation between layered networks[J].Physical Review E, 2011,84(2):e026101

[16] ZHAN W H,ZHANG Z Z,GUAN J H,et al.Evolutionary method for finding communities in bipartite networks[J].Physical Review E,2011,83(6):066120.

[17] LUO L,CHEN X S.Chain formation in a monolayer of dipolar hard spheres under an external field[J].Science China:Physics Mechanics&Astronomy,2011,54 (9):1555-1560.

[18] DENGW,LI W,CAI X,et al.On the application of the cross-correlations in the Chinese fund market:Descriptive properties and scaling behaviors[J].Advances in Complex Systems,2011,14(1):97-109.

[19] CUI L Y,LIU F,OU-YANGZC.The study of the elasticity of spider dragline silk with liquid crystal model [J].Thin Solid Films,2009,518(2):735-738.

[20] SONG D M,TUMMINELLO M,ZHOU W X,et al.Evolution of worldwide stock markets,correlation structure,and correlation-based graphs[J].Physical Review E,2011,84(2):026108.

[21] WANG W,CHEN Y,HUANG J P.Heterogeneous preferences,decision-making capacity and phase transitions in a complex adaptive system[J].Proceedings of the National Academy of Sciences of the United States of America,2009,106(21):8423-8428.

[22] ZHAO L,YANGG,WANG W,et al.Herd behavior in a complex adaptive system[J].Proceedings of the National Academy of Sciences of the United States of A-merica,2011,108(37):15058-15063.

[23] GAO Y,HUANG J P,LIU Y M,et al.Optical negative refraction in ferrofluids with magneto-controllability [J].Physical Review Letters,2010,104(3):034501.

[24] HUANGJ P,YU K W.Enhanced nonlinear optical responses of materials:Composite effects[J].Physics Reports,2006,431(3):87-172.

[25] HUANGJ P,YU K W.New nonlinear optical materials:Theoretical research[M].New York:Nova Science Publishers,Inc.,2007.

Some emergent features based on couplings between fields and structures in complex systems and their physical mechanisms

HUANGJi-ping
(Departmemt of Physics,Fudam Umiversity,Shamghai 200433,Chima)

It is of importance to investigate the effect of couplings between fields and structures on emergent properties of complex systems,because such couplings can be used to describe one of the common features of various complex systems.Namely,these systems have two basic interactions, one of which is the interaction between individuals,and the other of which is the interaction between individuals and environments.Here,some emergent features of complex systems were reviewed with a focus on the effect of such couplings.These emergent features are not only useful for developing specific systems,but also of potential value for establishing the universal theory for describing various kinds of complex systems.

emergemcy；complexity；statistical physics

N 94文献标示码：A

1007-6735(2011)05-0418-07

2011-09-16

国家自然科学基金资助项目(11075035,10874025)

黄吉平(1977-),男,教授.研究方向:软物质与交叉学科.E-mail:jphuang@fudan.edu.cn