一类含潜伏时滞的SIS传染病模型的定性研究

赵 瑜, 原三领, 李 盼

(1.宁夏师范学院数学与计算机科学学院,宁夏 756000；2.上海理工大学理学院,上海 200093)

一类含潜伏时滞的SIS传染病模型的定性研究

赵 瑜1, 原三领2, 李 盼2

(1.宁夏师范学院数学与计算机科学学院,宁夏 756000；2.上海理工大学理学院,上海 200093)

利用构造Liapunov泛函的方法,研究了一类含有潜伏期时滞的SIS传染病模型.得到了地方病平衡点和无病平衡点局部及全局渐近稳定的充分条件;当时滞超过某一临界值时,地方病平衡点失去稳定性,通过Hopf分支在其附近跳出极限环.揭示了时滞对疾病传播的影响.

传染病模型;时滞;Liapunov泛函;稳定性;Hopf分支

由于人类或动物侵入新的生态系统、全球变暖、环境退化、国际旅行增加等因素的影响,将增大新产生或已存在的传染病流行的机会.数学建模已经成为分析流行病传播和控制的重要工具[1].文献[2]考虑了一类具有染病期时滞和常数人口输入的SIS传染病模型,文_献[3]考虑了两类具有染病期时滞的SIS传染病模型.文献[4]考虑了具有时滞和总人口变动的SIS传染病模型,类似的还可参见文献[5-10].

在通常的SIS传染病模型中,易感者被感染后成为染病者,染病者康复后又再次成为易感者.在以往考虑的有关SIS模型的文献中大多假设易感者与染病者充分接触后立即成为染病者,未考虑易感者被疾病感染后的潜伏过程.本文在以往文献的基础上,假设易感者被感染后不是立即对外呈现传染力,而是具有一定的潜伏时间,并把此考虑为时滞因素,建立了一类含有相当于潜伏期时滞的SIS传染病模型.利用构造Liapunov泛函的方法,得到了各类平衡点局部和全局渐近稳定的充分条件；当时滞超过某一临界值时,地方病平衡点失去稳定性,通过Hopf分支在其附近跳出极限环,疾病的传播会呈现周期性的振荡现象.

1 模 型

假设t时刻总人口为N(t),把总人口分为易感者类,染病者类,即N(t)=S(t)+I(t),其中S(t) 和I(t)分别表示t时刻易感者类和染病者类的数量,考虑模型

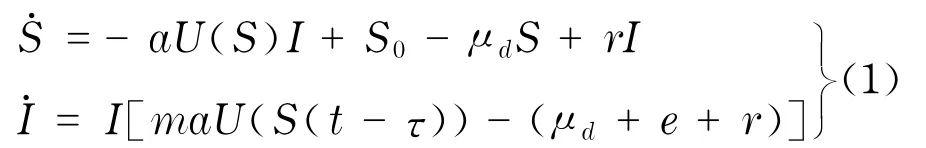
其中,所有的参数均为正常数.a为疾病最大传染力；S0为人口的净迁入；μd为人口的自然死亡率；r为疾病的恢复率；e为因病死亡率；τ为易感者感染疾病后的潜伏期；m为易感者被感染经潜伏期后进入染病者类的比率；aU(S)表示染病者具有的传染力,且满足

2 正平衡点的稳定性

2.1 正平衡点E*的局部稳定性

首先考虑正平衡点E*=(S*,I*)的局部稳定性,令

由式(12)可证明如下结论:

证明 设(x1(t),x2(t))是系统(7)的任一解, 令T0＞τ,对式(12)的两边由T0到t(≥T0)积分,得到

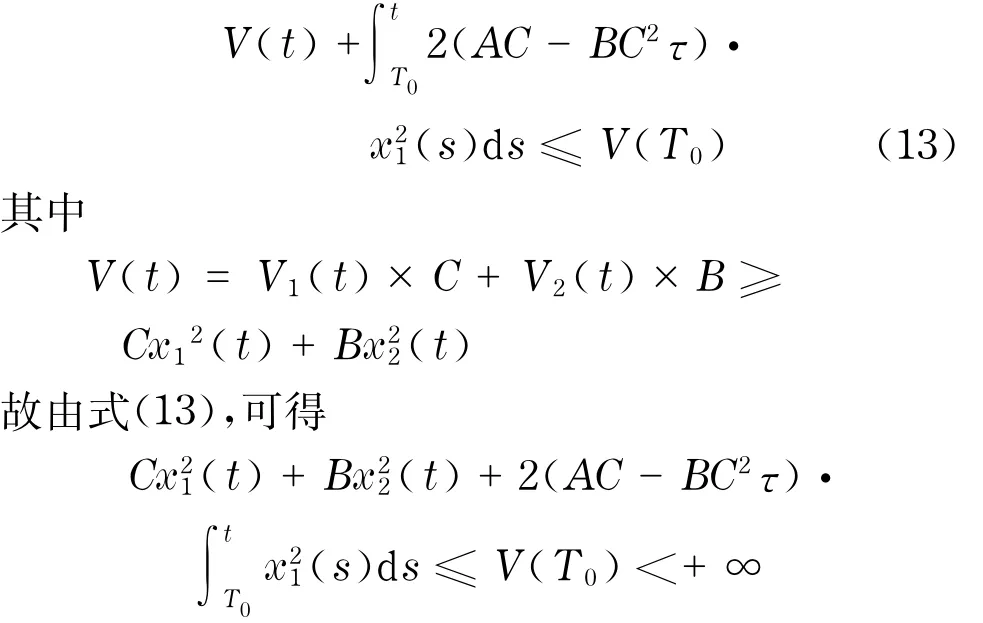
因此x1(t)和x2(t)是有界的,并且x1(t)∈L1[0,∞),由系统(7)和中值定理有x1(t),x2(t)及其微分泛函在[0,∞)上是一致连续的.由Barbalat引理(见Gopalsamy[9]引理1.2.2和1.2.3),可得当t→∞时,(x1(t),(t))→0.因此由系统(7)的第一个方程,可得

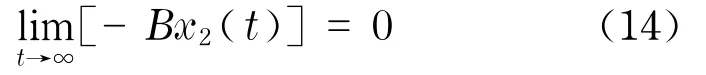
即当t→∞时,x2(t)→0.因此对系统(7)的任一解都有(x1(t),x2(t))→0(t→∞).

2.2 正平衡点E*的全局渐近稳定性

为了研究E*的全局稳定性,考虑系统(1)的任一正解X(t)=(S(t),I(t)).做变换

且对任意的x1∈[-S*,+∞]都有x1ξ(x1)＞0,当且仅当x1=0时,x1ξ(x1)=0.由式(15),系统(1)可写成

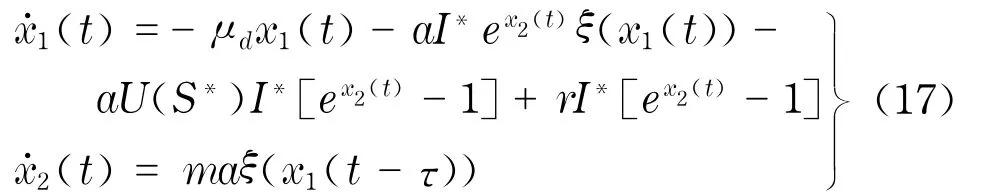
此时,系统(1)的正平衡点被变换成系统(17)的平衡点(0,0).

定理2 如果μd+e+r＜ma,S0＞μdS*, Tr＜1,则正平衡点E*是全局渐近稳定的.其中

证明 首先,证明E*是全局吸引的.令(x1(t),x2(t))是系统(17)的任一解,考虑泛函

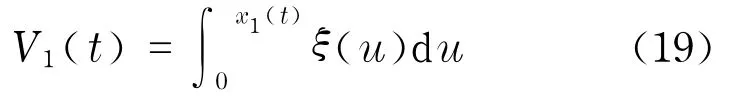
则V1(t)≥0,当且仅当x1(t)=0时V1(t)=0.沿着系统(17)的解求导,可得

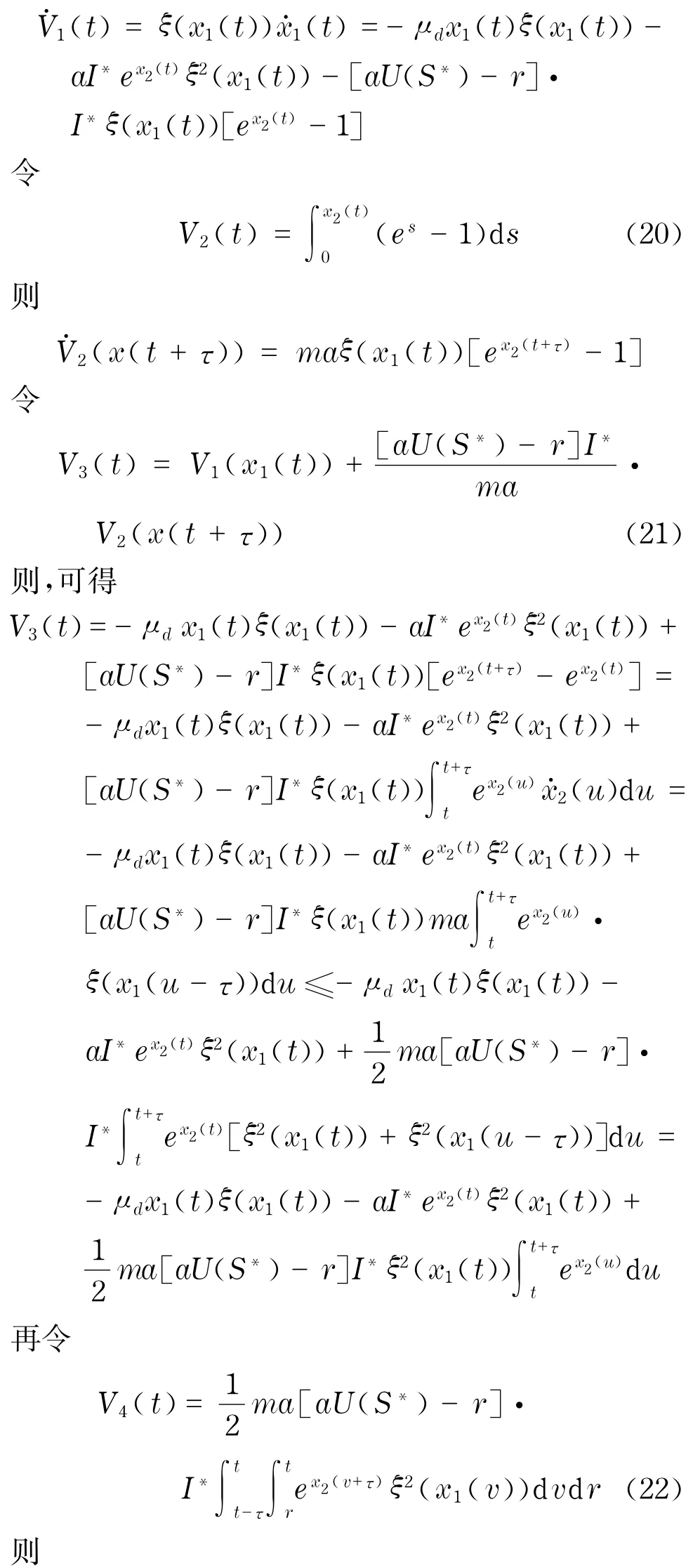
类似于定理1的证明过程,可以证明当Tr＜1时,正平衡点E*是全局吸引的.又由定理1,E*是局部渐近稳定的,因此E*是全局渐近稳定的.

3 E*处的Hopf分支

系统(7)的特征方程为

4 无病平衡点E0的稳定性

5 讨 论

将易感者被感染后的潜伏期作为时滞因素,考虑了一类含时滞的SIS传染病模型.利用构造Liapunov泛函的方法,得到了各类平衡点局部和全局渐近稳定的条件:如果μd+e+r＞ma,无病平衡点E0是全局渐近稳定的；如果μd+e+r＜ma, S0＞μdS*,Tr＜1,则正平衡点E*是全局渐近稳定的.当τ∈(0,τ0)时,平衡点E*是稳定的,当τ＞τ0时,平衡点E*失去稳定性,且系统(1)在τ0附近从E*处通过Hopf分支产生周期解,此时,疾病的传播呈现周期性的振荡现象.

[1] 马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].北京:科学出版社,2004.

[2] COOKE K L,YORKE J A.Some equations modeling growth processes and gonorrhea epidemics[J].Math Biosci,1973,16(1/2):75-101.

[3] HETHCOTE H W.The mathematics of infectious diseases[J].SIAM Review,2000,42(4):599-653.

[4] HETHCOTE H W,DRIESSCHE P van den.Two SIS epidemiologic models with delays[J].J Math Biol, 2000,40(1):3-26.

[5] YUAN San-ling,MA Zhi-en.Global stability and Hopf bifurcation of an SISepidemic model with time delays [J].Journal of Systems Science and Complexity,2001, 14(3):327-336.

[6] YUAN San-ling,MA Zhi-en,JIN Zhen.Persistence and periodic solution on a nonautonomous SIS model with delays[J].Acta Mathematicae Applicatae Sinica,2003, 19(1):167-176.

[7] 胡宝安,孙利民,夏爱生,等.一类时滞SIS传染病模型的讨论[J].数学研究,2007,40(1):103-108.

[8] 赵瑜,原三领,李盼.一类具有染病者隔离的非线性传染病模型的研究[J].上海理工大学学报,2009,31 (5):414-416.

[9] 周艳丽,王美娟.含时滞具有饱和传染率的SIQRS接种传染病模型[J].上海理工大学学报,2009,31(5): 417-421.

[10] YANG Kuang.Delay Differential Equation with Applications in Population Dynamics[M].Boston:Academic Press,1993.

[11] MARSDEN J E,MCKRACKEN M.The Hopf Bifurcation and its Applications[M].New York: Springer,1976.

Qualitative analysis of an SIS epidemic model with latent delay

ZHAOYu1, YUANSan-ling2, LIPan2
(1.School of Math amd Computer Sciemce,Nimgxia Teachers College,Nimgxia 756000,Chima；2.College of Sciemce,Umiversity of Shamghai for Sciemce amd Techmology,Shamghai 200093,Chima)

An SISepidemic model with a delay corresponding to the latent period was investigated. By means of constructing Liapunov functionals,some sufficient conditions for the local and global stability of the endemic equilibrium and the disease-free equilibrium were obtained,respectively. When the delay increases above some threshold,the endemic equilibrium loses its stability and Hopf bifurcation occurs,i.e.,a family of periodic solutions bifurcates from the endemic equilibrium.The effect of the delay on the spread of disease was disclosed.

epidemic model；delay；Liapumov fumctiomal；stability；Hopf bifurcatiom

O 175.1文献标示码：A

1007-6735(2011)05-0480-05

2009-12-09

国家自然科学基金资助项目(10871129)；上海市教委专项基金资助项目(09YZ208)；宁夏自然科学基金资助项目(NZ102228)

赵 瑜(1982-),男,讲师.研究方向:生物数学.E-mail:zhaoyuzy123@163.com

原三领(联系人),男,副教授.研究方向:微分方程与动力系统、生物数学.E-mail:yuansanling@263.net