拥塞服务网络上的寡头竞争

胡一竑, 干宏程, 张建同

(1.同济大学经济与管理学院,上海 200092;2.上海理工大学超网络研究中心,上海 200093)

拥塞服务网络上的寡头竞争

胡一竑1, 干宏程2, 张建同1

(1.同济大学经济与管理学院,上海 200092;2.上海理工大学超网络研究中心,上海 200093)

研究拥塞服务网络中寡头快递服务商关于价格竞争的均衡问题.描述了拥塞服务网络并构建了寡头服务商竞争的二层均衡EPEC模型.证明了寡头服务商竞争的Nash均衡的性质以及存在性.给出简单算例.研究结果对服务网络环境下的寡头服务商竞争有借鉴意义.

拥塞服务;变分不等式;Wardrop均衡;Nash均衡

考虑拥塞服务网络上寡头服务商的价格竞争均衡问题.很多现代服务业具有拥塞效应,如交通网络、物流运输网络、电力网络、计算机网络等等,在这些服务网络上由于拥塞效应的存在,使用者的选择

具有负的网络外部性,即使用者选择某条服务路径或服务产品将给其他使用者带来成本增加.在服务网络上的寡头服务提供商具有服务路径的控制权,对使用者收取服务费用,服务商之间互相以价格进行竞争,以求实现各自的利润最大化.服务商的价格决策影响使用者的选择,因此他们做决策时预先将使用者反应考虑在内.典型的例子如交通网络中的收费道路[1]、无线接人网络服务商[2]、电力网络中的电力提供商[3]及物流网络中的物流运输公司[4]等等.地面交通是典型的拥塞性网络,私家车出行会根据出行成本最小选择相应的道路,收费道路在制定过路费的时候将考虑行人的选择,以及和它平行竞争的其它收费道路的决策.又如无线网络发展迅速,网络商的竞争也日益激烈,接人网络中某接人点的使用人数增加将降低接人速度,从而影响顾客选择.所以无线网络服务商的价格制定也将考虑顾客选择和竞争对手的价格决策.本文将研究在这种具有拥塞特性的服务网络中对服务路径拥有控制权的寡头服务商之间的价格竞争和均衡问题.

国外近年来有不少文献研究拥塞服务业竞争. Acemoglu等[5]研究平行边上以价格进行竞争的寡头企业的均衡问题,顾客根据效用最大化进行路径选择,当效用为零时顾客选择退出.而后他们[6]将其推广到平行路径上包含有序贯边的网络结构.Xiao等[1]针对私营收费道路这一典型的拥塞服务业,研究以过路费和道路容量投资进行竞争的寡头企业的Nash均衡.他们以行人的Wardrop均衡为下层约束,以私人寡头企业竞争为上层问题,研究得到随着竞争者数量增多、寡头竞争趋向完美竞争时,过路费和道路容量都趋向于社会最优的结论.Xiao并没有给出寡头竞争Nash均衡的存在性证明,这一问题在Johari等[7]中得到了解决.Johari等研究不同的投资回报率情况下服务商的服务能力投资决策和市场均衡结构,给出Nash均衡的存在性和唯一性证明,并扩展研究了服务商的市场进人决策.Cominetti等[4]以物流运输网络为背景,研究以价格和服务水平(即运送时间)竞争的寡头物流公司之间的Nash均衡.这些现有文献对于拥挤服务竞争都采用二层均衡的结构,即在考虑消费者均衡的前提下考虑服务商的竞争和均衡.国内据作者所知还未看到相关文献.

本文旨在分析由平行边组成的拥塞服务网络上服务商竞争均衡模型.考虑拥塞服务业中由多家寡头服务商为消费者提供具有拥塞特性的服务,面对的是固定需求的服务需求市场.整个过程是领导者-跟随者两阶段博弈,领导者服务商之间互相以服务价格相互竞争,从利润最大化出发做战略性的定价决策.服务价格决定后,需求市场上的消费者根据自己成本最小化选择服务产品,由于拥塞性的存在,消费者的决策相互影响,存在市场均衡.因此问题可以在数学上描述为二层均衡EPEC模型(equilibrium problems with equilibrium constraints),上层是服务商竞争的Nash均衡,下层是消费者的Wardrop均衡,如图1所示.下层均衡用变分不等式来进行描述.关于EPEC模型的均衡求解和计算,目前学术界还处在起步阶段,Su[8]和Andrew[9]提出了NCP算法、演化多目标优化算法等求解方法.本文只给出服务商竞争均衡的存在性证明,具体均衡的计算方法可参见这些文献.

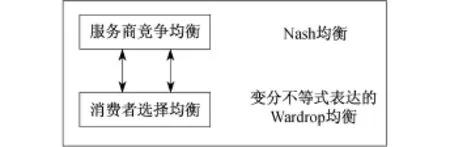
图1 拥塞服务网络中的寡头服务商竞争示意图Fig.1 Oligopolistic competition in service network with congestion

1 拥塞服务网络均衡模型

首先描述拥塞服务网络模型,在此基础上建立服务商竞争的模型.假设服务市场由n个服务提供商构成,提供可替代的服务给顾客.顾客在不同的服务之间进行选择以最小化其成本,由于拥塞性的存在,个人选择彼此影响选择结果聚集后构成市场均衡.

数学符号和决策变量：d为总市场需求;Xi为选择服务i的顾客人数;pi为服务商i的服务价格;Fi(Xi)为服务i的延迟时间成本函数,是Xi的函数.

假设顾客是完全理性的,每一位顾客依循自己成本最小化原则选择服务,而所有的选择某服务的顾客人数就是该服务的市场份额.将消费者对服务的选择问题转化为出行者的道路选择问题,见图2 (见下页).其中第i条道路的出行成本等于消费者选择第i种产品的负效用.消费者选择道路i,等同选择服务i.假设有一群出行者要从O地到D地去,在选择道路的时候,消费者会首先选择成本最低的道路,随着选择人数逐渐增多,超过该道路正常服务能力而变得拥挤,提高了消费者感知到的服务成本.消费者将转而选择效用较高的道路,直至该道路又开始变得拥挤.消费者的成本最小化选择受道路流量影响,消费者的选择又影响了流量.如此经过一段时间,交通网络达到一种均衡状态,每条有行人走的道路上出行成本都相同,而无人走的道路出行成本必定高于有人走的道路,单个出行者不能通过单方面改变自己的选择而降低出行成本,即达到了Wardrop均衡.均衡时,道路上的交通流量等同服务的市场份额.

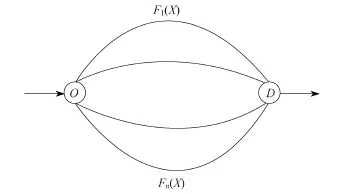
图2 由平行边组成的拥塞服务网络Fig.2 Service network composed of parallel links with congestion

首先给出关于服务的延迟时间函数的假设,再给出Wardrop均衡定义.

条件1延迟时间函数Fi(xi)是连续可微、严格递增的凸函数.

定义1(Wardrop均衡)对于给定的价格p,如果xOE满足下述的变分不等式(1),就称xOE是Wardrop均衡解.记给定价格p下的Wardrop均衡解为W(p).

该变分不等式的经济含义是：当服务需求市场中顾客的选择达到均衡时,在其他顾客不改变选择的请求下,单个顾客不能通过单独改变选择而使其成本降低.此时顾客的选择是使其成本达到最大的选择.

对于下层服务需求市场上顾客选择的均衡存在性和唯一性,许多文献已经做过深人讨论,这里简述如下,不做证明.

定理1 (WE均衡存在性和唯一性)当延迟时间成本函数Fi(xi)满足条件1时,存在唯一的Wardrop均衡.

下层问题达到Wardrop均衡时,弧上的流量应该满足条件

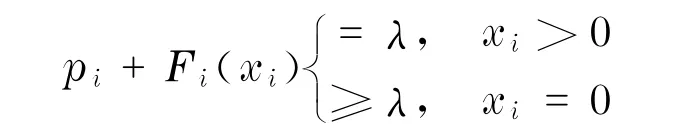
式中,λ为最低的服务成本.该式在后面的分析中较为方便,因此将用此均衡条件表示Wardrop均衡.

2 服务商竞争均衡

假设服务商对市场需求、消费者反应完全了解,具有完全信息,在消费者选择之前决定他的服务能力,然后消费者再进行对服务的选择,这样构成一个有前后次序的博弈过程,本质上是两阶段Stackelberg博弈.服务商在决策过程中拥有较高的决策权,是主导者,消费者处于从属地位,是博弈的从属者.讨论服务商价格竞争的Nash均衡的性质和存在性.首先给出关于寡头Nash均衡的定义.

命题1纯策略寡头均衡时,记A为均衡流量大于零的弧的下标集合,则均衡价格和均衡流量之间满足关系

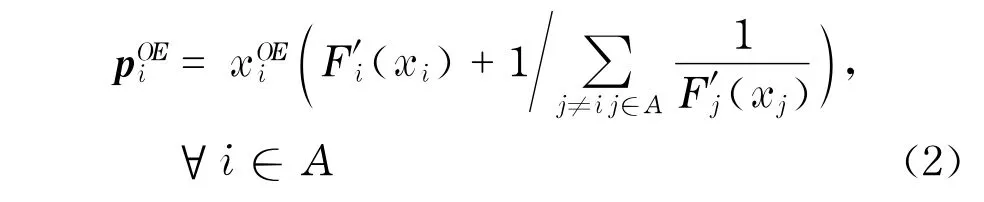
证明不失一般性,假设1属于A.则可以写出其他服务商价格给定下服务商1的优化问题

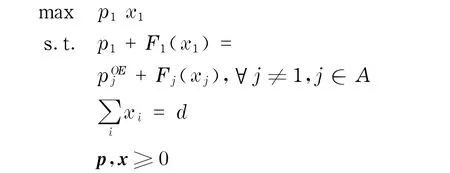
容易验证,此约束条件满足约束规格,因此KKT条件是最优解的必要条件[10].若记μj和λ为相应约束条件的拉格朗日乘子,那么目标函数可以写成定理2寡头服务商的价格竞争存在纯策略寡头均衡(pOE,xOE).

证明 利用角谷静夫不动点定理来证明.令BS()为给定其他所有服务商的价格情况下服务商s的最优价格反应映射.也就是说,对于某个服务商s来说,BS()是优化问题的解

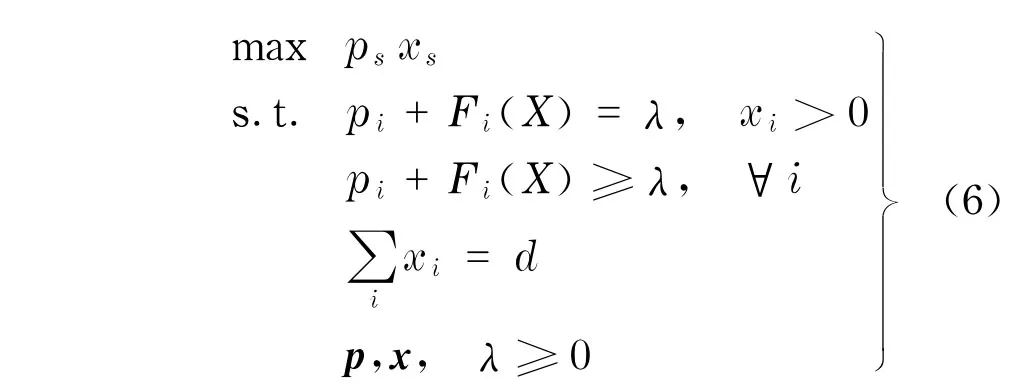
3 算 例

考虑一个简单的类似Pigou网络的算例.假设市场上有2家寡头服务商,总需求是1.如图3,路径的成本函数分别为1和k X,总流量为1.不考虑服务商收费的时候,可以通过Wardrop均衡得到路径上的流量分配为((k-1)/k,1/k),社会总成本为1.此时所有的消费者都选择下面的边,两条边上的边际成本相等,达到均衡状态,任何消费者都不愿再改变自己的选择.

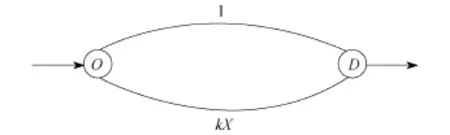
图3 算例图示Fig.3 A simple example

系统最优(社会总成本最低)时,假设有个中央控制者以最小化社会成本为出发点做路径选择决策,可以得到最优流量为((2k-1)/2k,1/2k),社会总成本为(4k-1)/4k.现在考虑网络上的边由不同寡头服务商控制并分别向消费者收取费用,以最大化各自利润为出发点做价格决策.通过简单的计算可以得到,服务商1的最优价格反应函数p1应为(p2+k-1)/2,服务商2的最优价格反应函数p2应为(p1+1)/2,则两个服务商的Nash均衡价格应为((2k-1)/3,(k+1)/3),相应流量分配为((2k-1)/3k,(k+1)/3k).此时若不考虑服务商和消费者之间的支付转移,则社会总成本为(k2+8k-2)/9k.将系统最优和寡头竞争情况做对比,可以看到由于寡头服务商追求自身利益最大化,不考虑自身设定价格的决策对其他服务商和消费者的影响,所以通过收费将流量从道路1推向道路2,提高了社会总成本,造成了效率损失.

4 结 论

研究拥塞服务网络中的寡头服务商之间的竞争均衡问题.将问题构建成数学上的二层均衡问题(EPEC问题).下层顾客根据自己成本最小原则进行服务选择,由于拥塞特性的存在,顾客选择彼此影响形成均衡.上层寡头服务商基于价格进行竞争,利用角谷静夫不动点定理证明了Nash均衡存在性,并给出均衡时的均衡价格的性质.最后给出简单算例,并进行了讨论.在本文建立了服务商竞争均衡的基础上,可以进行更一步的深人分析,如寡头竞争相对社会福利的效率损失、寡头服务商的竞争策略设计等.

[1] XIAO F,YANG H,HAN D.Competition and efficiency of private toll roads[J].Transportation Research Part B,2007,41：292-308.

[2] DUSIT N,EKRAM H.A game theoretic analysis of service competition and pricing in heterogeneous wireless access networks[J].IEEE Transactions on Wireless Communications,2008,7(12)：5150-5155.

[3] COMINETTI R,CORREA J R,STIER-MOSES N E. The impact of oligopolistic competition in networks [J].Operations Research,2009,57(6)：1421-1437.

[4] ACEMOGLU D,OZDAGLAR A.Competition and efficiency in congested markets[J].Mathematics of Operations Research,2007,32(1)：1-31.

[5] ACEMOGLU D,BIMPIKIS K,OZDAGLAR A.Price and capacity competition[J].Games and Economic Behavior,2009,66(1)：1-26.

[6] ACEMOGLU D,OZDAGLAR A.Competition in parallel-serial networks[J].IEEEJournal on Selected Areas in Communications,Special Issue on Non-Cooperative Behavior in Networking,2007,25(6)：1180-1192.

[7] JOHARI R,WEINTRAUB G Y,VAN R B.Investment and market structure in industries with congestion [J].Operations Research,2010,58(5)：1303-1317.

[8] SU Che-lin.Equilibrium problems with equilibrium constraints：stationeries,algorithm,and applications [D].Stanford：Stanford University,2005.

[9] ANDREW K,SHEPHERD S.Tolling,collusion and equilibrium problems with equilibrium constraints[J]. European Transport,2010,44：3-22.

[10] BERTSEKAS D P,NEDI'C A,OZDAGLAR A E.Convex Analysis and Optimization[M].Belmont：Athena Scientic,2003.

[11] BERGE C.Topological Space[M].New York：Reprint Dover Publication,1963.

Oligopoly competition in service networ ks with congestion

HUYi-hong1, GANHong-cheng2, ZHANGJian-tong1
(1.School of Economics and Management,Tongji University,Shanghai 200092,China; 2.Center for Supernetworks Research,University of Shanghai for Science and Technology,Shanghai 200093,China)

The price equilibrium between oligopoly service providers in service networks with congestions was studied.The bi-level MPEC model of service competition in service networks was described.The lower level is Wardrop equilibrium between customers,while the upper level is the Nash equilibrium between service providers.The existence of the price oligopoly equilibrium was proved and its properties were analysed.The practice in the express service industry in China was discussed.A numerical example was given to show that service providers should take the customer preference into consideration when making decisions.

service with congestion;variational inequality;Wardrop equilibrium;Nash equilibrium

N 94

A

1007-6735(2011)03-0292-05

2011-05-11

国家自然科学基金资助项目(70832005,71090404/71090400);高校博士点新教师基金资助项目(20100072120045)

胡一竑(1978¯),女,讲师,研究方向：物流供应链和服务科学.E-mail：yhhu@tongji.edu.cn.张建同(联系人),女,教授.研究方向：服务科学、统计学.E-mail：jtzhang@163.com