生产中断风险下的供应链网络设计

刘祖刚

(宾夕法尼亚州立大学黑泽尔顿分校商业与经济系,黑泽尔顿PA 18202)

生产中断风险下的供应链网络设计

刘祖刚

(宾夕法尼亚州立大学黑泽尔顿分校商业与经济系,黑泽尔顿PA 18202)

主要研究生产中断风险下的供应链网络设计问题.基于超网概念和变分不等式的理论构建供应链网络模型,模型包括多个供应商和制造商并且考虑生产中断的风险对供应链中决策者成本、利润以及生产网络产能设计的影响.使用变分不等式的形式来表达网络均衡状态下的各个决策者的最优解.同时还提供了模型解存在性证明以及变分不等式函数的单调性证明.

供应链;生产中断风险;超网;变分不等式

供应链网络设计与优化在近年来成为越来越受关注的领域.文献中大多数的研究都是集中于单一公司的供应链设计决策问题并且一般使用另一变量或者整数变量建构模型.对于这一领域的研究和模型读者可以参考文献[1-4]概述和讨论.Nagurney[5]研究了最优的供应链网络设计和再设计,考虑了需求满足的条件和最小化成本的目标.Nagurney[6]进一步讨论了多公司竞争下的供应链设计模型,基于变分不等式理论建模并且考虑了利润最大化的目标.Nagurney等在文献[7-8]中又分别研究了供应链设计中的可持续性问题以及生产外包和关键需求的满足问题.另外,近年来许多理论和应用研究从不同角度讨论了供应链中断风险以及相关的决策、成本以及影响.Craighead等[9]指出在当今的全球化环境中供应链中断导致的运营以财物风险是众多公司所面临的最具紧迫性的问题.Hendriks等[10]分析了800例供应链中断的案例.他们发现这些经历了供应链中断的公司的股票价格比同一领域的其它公司低30%～40%.Snyder等[11]提出了考虑供应风险的仓库位置选取模型更多有关供应链中断风险的研究可见文献[12-14].然而以上的研究主要集中在一个或两个公司的决策和分析.基于超网理论的模型为研究由众多不同公司组成的供应链网络的供应中断风险提供了可能.Nagurney等[15]考虑了供应链网络的供应风险和需求风险.Qiang等[16]提出的考虑供应中断的供应链网络模型,运用了多目标优化的方法并使用了成本的方差来衡量风险. Cruz等[17]研究了供应中断风险与投机风险在多时期供应链网络中的关系与影响.笔者提出文献中首个考虑供应中断风险的供应链网络设计模型,定义所需的决策变量和成本函数并建构供应链网络设计模型.本模型不仅考虑供应中断风险并且考虑多个制造商之间的竞争,同时提供存在性和单调性的结果以及一个求解本模型的算法.

1 考虑供应中断风险的供应链网络设计模型

模型基于超网的概念以及变分不等式的理论[18-19].本文中的模型考虑n=1,…,N个供应商,m=1,…,M个制造商,如图1所示.下面将分别讨论供应商和制造商的决策过程和优化问题并且提出表达供应链网络均衡的变分不等式.

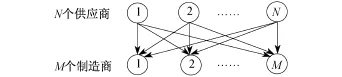
图1 供应链网络Fig.1 Supply chain network

1.1 供应商的决策和优化问题

每一个供应商n决定对每个制造商的供应量,本身生产总量qn,以及最大产能yn.另外,用表示供应商n与制造商m之间的交易价格,用hn(qn)表示生产成本函数,用gn(yn)表示产能建设成本,用cnm表示供应商n与制造商m之间的单位交易成本,用Kn表示最大产能.供应商n首先考虑利润最大化并优化问题

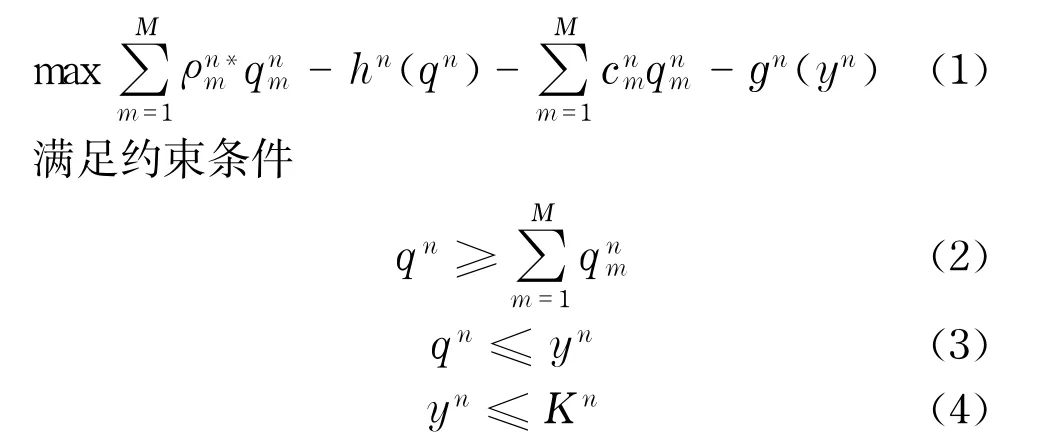
供应商n还需要考虑生产中断风险rn.用生产中断导致的惩罚期望值来表示生产中断风险.用fn(x)表示供应商无中断生产x的概率密度,使用wn表示单位惩罚.中断风险可表示为

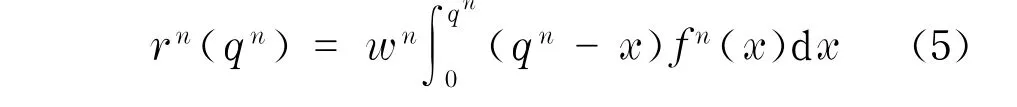
引理1供应商生产中断风险rn是qn的凸函数.

证明

现在综合利润最大化和风险最小化供应商n的最优化问题可表示为

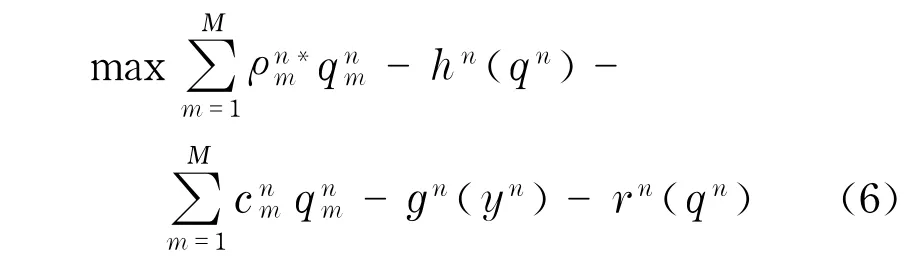
满足拘束条件式(2)～(4).

现在假设所有供应商的成本函数都是凸函数并且所有供应商都采取不合作的纳什均衡方式竞争.用Q1表示所有qn的矢量,用Q2表示所有qnm的矢量,用Y1代表所有yn的矢量.那么根据文献[18]和文献[20-21]所有供应商的最优化条件同时可表示为如下变分不等式：决定(Q1*,Q2*,Y1*)∈K1,满足条件

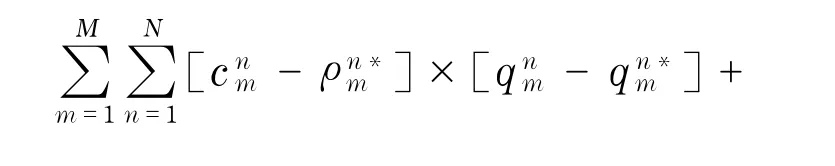
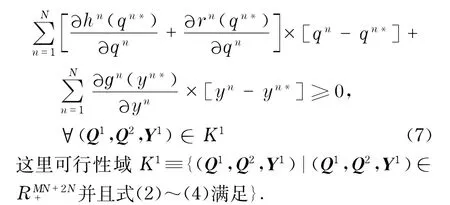
1.2 制造商的决策和优化问题

每一个制造商m决定从每个供应商的的交易量,本身生产总量qm,以及最大产能ym.另外,用表示供应商n与制造商m之间的交易价格,用hm(qm)表示生产成本函数,用gm(ym)表示产能建设成本,用Km表示最大产能,用vb表示单位产品所需材料,用Pm(qm)表示反需求函数.供应商n首先考虑利润最大化并优化问题制造商m还需要考虑生产中断风险rm.用生产中断导致的惩罚期望值表示生产中断风险.用fm(x)表示制造商无中断生产x的概率密度,用wm表示单位惩罚.中断风险可表示为

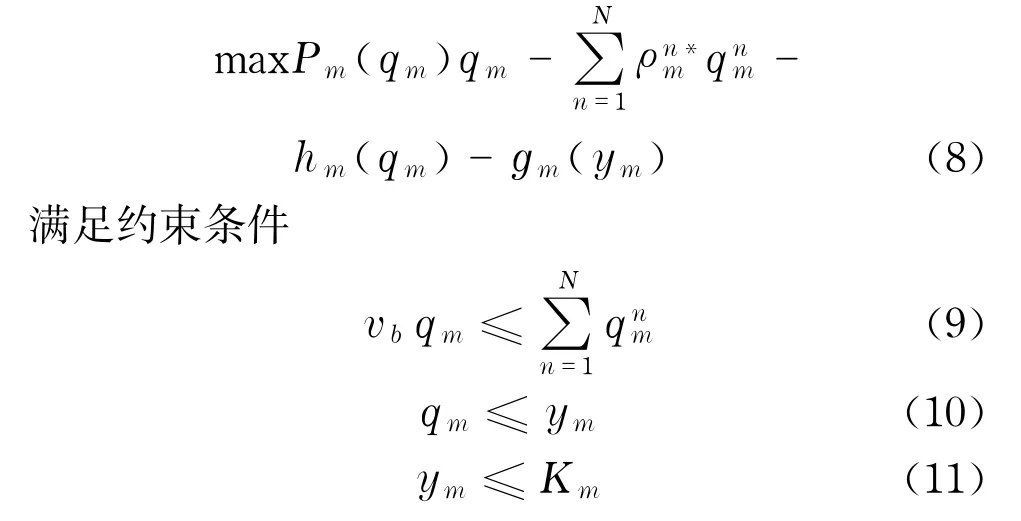
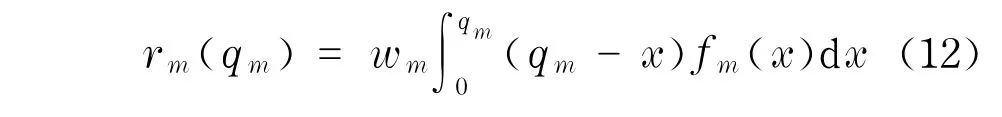
引理2制造商生产中断风险rm是qm的凸函数.

证明同引理1的证明.

现在综合利润最大化和风险最小化制造商m的最优化问题可表示为

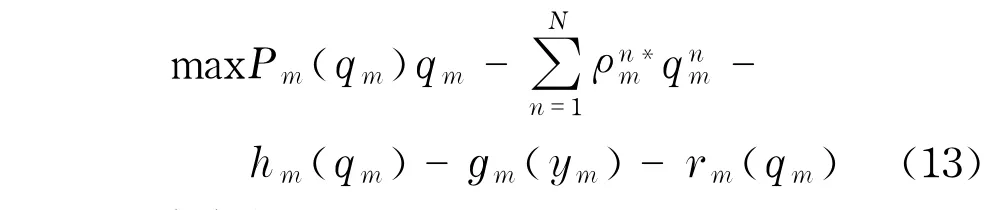
满足约束条件式(9)～(11).

现在假设所有制造商的成本函数都是凸函数,反需求函数都为减函数,并且所有制造商都采取不合作的纳什均衡方式竞争.用Q3表示所有qm的矢量,用Y2表示所有ym的矢量.那么根据文献[18]和文献[20-21]所有供应商的最优化条件同时可表示为变分不等式：决定(Q2*,Q3*,Y2*)∈K2,满足

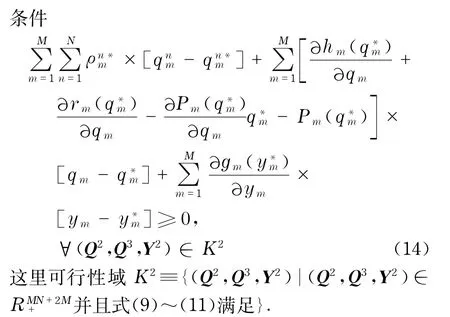
1.3 供应链网络的均衡条件

当整个供应链网络处于均衡状态下时,所有供应商的最优化条件以及所有制造商的最优化条件必须同时满足以至于没有决策者有改变决定的意愿.另外每个供应商送出到每个制造商的材料数量必须与每个制造商所受到的材料数量吻合.

定义1在考虑供应中断和网络设计条件下整个供应链网络的均衡满足式(7)与式(14)的总和.在这种情况下所有决策者都没有单方改变决定的意愿.

定理1(变分不等式形式)

考虑供应中断和网络设计条件下整个供应链网络的均衡条件可表示为变分不等式：决定(Q1*, Q2*,Q3*,Y1*,Y2*)∈K3,满足条件

证明首先将式(7)和式(14)加在一起得到式(15),再在式(15)的第一项中加人等于0,并不能改变式(15).加人+变分不等式可拆分成式(7)和式(14).

2 解的存在性和单调性

定理2(存在性)

假设成本函数,反需求函数都是连续的.变分不等式(15)存在一个解.

证明由于左右的决策变量都有上限式(15)的可行性域是封闭的和有限的.所以式(15)存在至少一个解[18].

定理3(单调性)

假设所有的成本函数是凸函数(含线形),反需求函数是线性减函数.则F(U)是单调的.F(U)的Jacobian矩阵是半正定的.

证明依据引理1和引理2可知风险函数是凸函数.于是可以验证F(U)的Jacobian矩阵是半正定的.由此导出F(U)是单调的.

所提出的模型可用Modified Projection Method求解[18].如果F(U)是单调的和Lipschitz连续该方法保证会收敛于一个解.

3 结 论

提出了一个考虑供应风险和网络设计的供应链网络均衡模型.使用了超网的概念和变分不等式来表示此供应链网络的均衡状态.本文同时还提供了模型解的存在性以及函数单调性的结论并且提出了求解方法.

[1] BEAMON B M.Supply chain design and analysis：Models and methods[J].International Journal of Production Economics,1998,55(3)：281-294.

[2] MIN H,ZHOU G.Supply chain modeling：past,present,future[J].Computers and Industrial Engineering, 2002,43(1/2)：231-249.

[3] MEIXELL M J,GARGEYA V B.Global supply chain design：A literature review and critique[J].Transportation Research E,2005,41(6)：531-550.

[4] GEUNESJ,PARDALOSP M.Network optimization in supply chain management and financial engineering： An annotated bibliography[J].Networks,2003,42(2)： 66-84.

[5] NAGURNEY A.Optimal supply chain network design and redesign at minimal total cost and with demand satisfaction[J].International Journal of Production E-conomics,2010,128(1)：200-208.

[6] NAGURNEY A.Supply chain network design under profit maximization and oligopolistic competition[J]. Transportation Research E,2010,46(3)：281-294.

[7] NAGURNEY A,NAGURNEY S.Sustainable supply chain network design：A multicriteria perspective[J]. International Journal of Sustainable Engineering, 2010,3(3)：189-197.

[8] NAGURNEY A,YU M,QIANG Q.Supply chain network design for critical needs with outsourcing[J]. Papers in Regional Science,2011,90(1)：123-142.

[9] CRAIGHEAD C W,BLACKHURST J,RUNGTUSANATHAM M J,et al.The severity of supply chain disruptions：Design characteristics and mitigation capabilities[J].Decision Sciences,2007,38(1)：131-156.

[10] HENDRICKS K B,SINGHAL V R.An empirical analysis of the effect of supply chain disruptions on longterm stock price performance and risk of the firm[J]. Production and Operations Management,2005,14(1)： 35-52.

[11] SNYDER L V,DASKIN M S.A reliability model for facility location：the expected failure cost case[J]. Transportation Science,2005,39(3)：400-416.

[12] GUPTA D.The(Q,r)inventory system with an unreliable supplier[J].INFOR,1996,34：59-76.

[13] PARLAR M,PERRY D.Inventory models of future supply uncertainty with single and multiple suppliers [J].Naval Research Logistics,1996,43(2)：191-210.

[14] TANG CS.Robust strategies for mitigating supply chain disruptions[J].International Journal of Logistics,2006,9(1)：33-45.

[15] NAGURNEY A,CRUZ J,DONG J,et al.Supply chain networks,electronic commerce,and supply side and demand side risk[J].European Journal of Operational Research,2005,164(1)：120-142.

[16] QIANGQ,NAGURNEY A,DONGJ.Modeling of supply chain risk under disruptions with performance measurement and robustness analysis[C]∥WU T,BLACKHURST J.Managing Supply Chain Risk and Vulnerability：Tools and Methods for Supply Chain Decision Makers.Berlin：Springer,2009：91-111.

[17] CRUZ J M,LIU Z.Modeling and analysis of the multiperiod effects of social relationship on supply chain networks[J].European Journal of Operational Research,2011,214(1)：39-52.

[18] NAGURNEY A.Network Economics：A Variational Inequality Approach[M].2nd.Dordrecht：Kluwer Academic Publishers,1999.

[19] NAGURNEY A,DONG J.Supernetworks：Decision-Making for the Information Age[M].Cheltenham： Edward Elgar Publishing Inc,2002.

[20] BAZARAA M S,SHERALI H D,SHETTY C M.Nonlinear Programming：Theory and Algorithms[M].New York：John Wiley&Sons,1993.

[21] GABAY D,MOULIN H.On the uniqueness and stability of Nash equilibria in noncooperative games[C]∥BENSOUSSAN A,KLEINDORFER P,TAPIERO C S.Applied Stochastic Control in Econometrics and Management Science.Amsterdam：1980,271-294.

Supply chain networ k design under production disruption risk

LIUZu-gang
(Department of Business and Economics,Pennsylvania State University,Hazleton,PA 18202,USA)

A model reguarding the supply chain network under production disruption risk was developed based on the concept of supernetworks and the theory of variational inequalities.The model consists of multiple suppliers and multiple manufacturers,and considers the impact of production disruption risks on the costs,profits,and capacity decisions of the supply chain firms.The variational inequality formulation was used to express the equilibrium conditions of the supply chain network where all decision makers'optimal conditions are simultaneously satisfied.The conditions for the existence of solution and conditions of monotonicity were provided.

supply chains;production disruption risk;supernetworks;variational inequality

N 94

A

1007-6735(2011)03-0264-04

2011-05-11

刘祖刚(1977¯),男,助理教授.研究方向：供应链管理、运输与物流、风险管理、运筹学等.E-mail：zxl23@psu.edu