基于模型预测控制的快速路网匝道调节方法

干宏程

(上海理工大学超网络研究中心,上海 200093)

基于模型预测控制的快速路网匝道调节方法

干宏程

(上海理工大学超网络研究中心,上海 200093)

探索了基于模型预测控制(MPC)的匝道调节方法.提出了匝道MPC调节的非线性动态时间离散最优控制模型及其解法.最优控制模型采用动态网络交通流模型作为过程模型,采用遗传算法求解.考察了匝道MPC调节的效果和鲁棒性,并将其效果与经典的ALINEA匝道调节方法相比.针对三起点三终点快速路网的仿真案例显示,匝道MPC调节能明显缓解拥堵,改善路网总体运行效率,较之ALINEA调节能够更连续平稳地调节交通流,在存在预测误差的情况下控制效果依然很好,其路网总耗时改善率明显高于ALINEA调节,具有很好的鲁棒性和应用前景.

匝道调节;模型预测控制;非线性优化;动态最优控制模型;遗传算法;鲁棒性

人口匝道调节(ramp metering)作为快速路控制的常见手段,一直是学术研究热点[1-11].动态的匝道调节方法主要有响应式(reactive)策略和最优控制(optimal control)策略两类.响应式策略的方法很多,如ALINEA法、需求容量法、各类启发式算法(如bottleneck法)、以及专家系统、神经网络、模糊控制等.不少实地研究显示,ALINEA法的控制效果在响应式方法中较为突出.最优控制力求从系统全局眼光将受控系统调控在最佳运行水平上.应用最优控制,需要有精确的过程模型(交通流模型).最优控制属于开环控制,实际应用时需将其置于滑动窗口(sliding horizon)框架下执行,以增强控制鲁棒性,这种执行方法称为模型预测控制(model predictive control,MPC).匝道MPC调节是当前研究前沿,国内外仅有少量研究报道[1-5],这些研究的仿真测试均显示了匝道MPC调节的良好应用前景.但是以往文献很少给出匝道MPC调节的鲁棒性分析.笔者紧跟研究前沿,探索匝道MPC调节方法,以期为实施先进匝道调节策略提供理论储备和技术参考.文中先阐述匝道MPC调节方法的基本原理,然后提出匝道MPC调节的数学模型及解法,针对算例路网测试匝道MPC调节的效果,并与ALINEA法的效果相比,最后考察匝道MPC调节的鲁棒性.

1 匝道MPC调节的基本原理

匝道MPC调节方法作为在线控制方法,在滚动窗口框架下执行最优控制方法.记滚动优化的周期为Ts,控制的离散时间标为ks.匝道MPC调节方法的运行结构如图1所示,其主要特点如下：

a.需要一个能够预测受控系统(快速路网)在给定控制信号(输人)作用下演化行为的时空离散模型,即快速路网交通流模型;

b.以某一性能指标最优为目标,考虑输人与输出的实际约束,求解所构造的非线性动态最优控制模型,得到的最佳控制信号作用于系统;

c.控制器每隔一个滚动周期(匝道调节率更新周期),根据交通实测数据确定系统当前状态,执行新的匝道调节率优化计算,优化计算所包含的预测时长为多个滚动周期,以考虑控制在今后相当长时间内的影响.优化得到的最优控制信号序列只实施预测时段中第一个滚动周期的信号.下一个滚动周期,控制器根据实测交通数据更新系统状态,重新执行优化计算,以此循环;

d.连接控制器与交通系统的闭环每隔一个滚动周期,把系统状态反馈给控制器,从而减少控制器预测误差的影响,使控制器具备自适应功能,能够通过更新过程模型及时考虑系统状态或系统参数的变化.

对于大型路网,为提高计算效率,每次滚动优化时可以只对预测时段的前若干个滚动周期的控制信号进行优化计算,其余控制信号恒定[2].

图1 匝道MPC调节的运行结构示意Fig.1 Schematic operational structure of MPC ramp metering

2 匝道MPC调节的数学模型

每一次滚动优化,都需求解带控制变量约束的离散时间动态非线性最优控制问题.极小化的目标函数

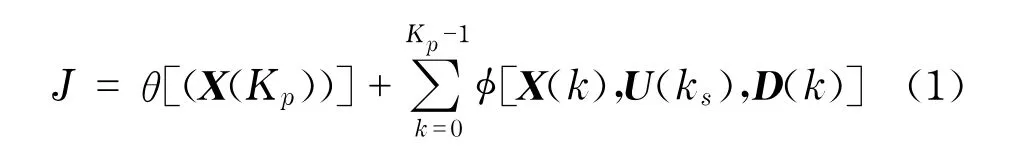
式中,φ、θ为任意的二次可微的非线性函数,具体形式根据交通管理需要设定.

过程模型(快速路网交通流模型)

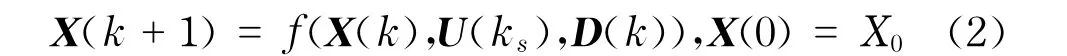
式中,X∈Rn为n维状态向量,由所有交通状态变量(如密度、速度、排队)组成.U为p维控制向量,由控制变量ui组成,i=1,2,…,p,p为需要实施调节的匝道个数.k为离散时间标,k=0,1,…Kp,Kp为预测时段长度.令T表示状态演化步距(即交通流模型取样周期).滚动优化周期Ts为T的整数倍,即Ts=zT,z为正整数,令ks=integer[k/z], integer表示取整;这表示实际控制中决策变量更新周期(几十秒到几分钟)通常是交通流模型取样周期(一般为10 s左右)的数倍.D由所有作用于过程的外扰(如交通需求)组成.

约束条件

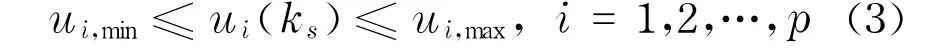
实际控制中,匝道MPC调节要决策的控制信号是取值域为[0,1]的匝道调节率,其物理意义为匝道信号灯周期内显示绿灯时间的比例.通常,ui,min=0,ui,max=1.

2.1 网络交通流模型

采用Papageorgiou提出的经典的多起点-多终点动态交通网络建模方法建立快速路网交通流模型[12-14],作为过程模型.交通流模型包含路段模型、节点模型、起点排队模型3部分,简述如下.

网络由节点和有向路段组成,节点为存在出(人)口匝道或道路属性发生变化的位置,路段是属性(如车道数、坡度)相同的一段道路,路段分为若干等长小段.例如,路段m分为Nm个长度为Δm的小段,小段车道数记为λm.路段m的第i小段在k时刻的交通状态用密度、速度和流量表示,分别记作ρm,i(k)、vm,i(k)和qm,i(k).

2.1.1 路段模型

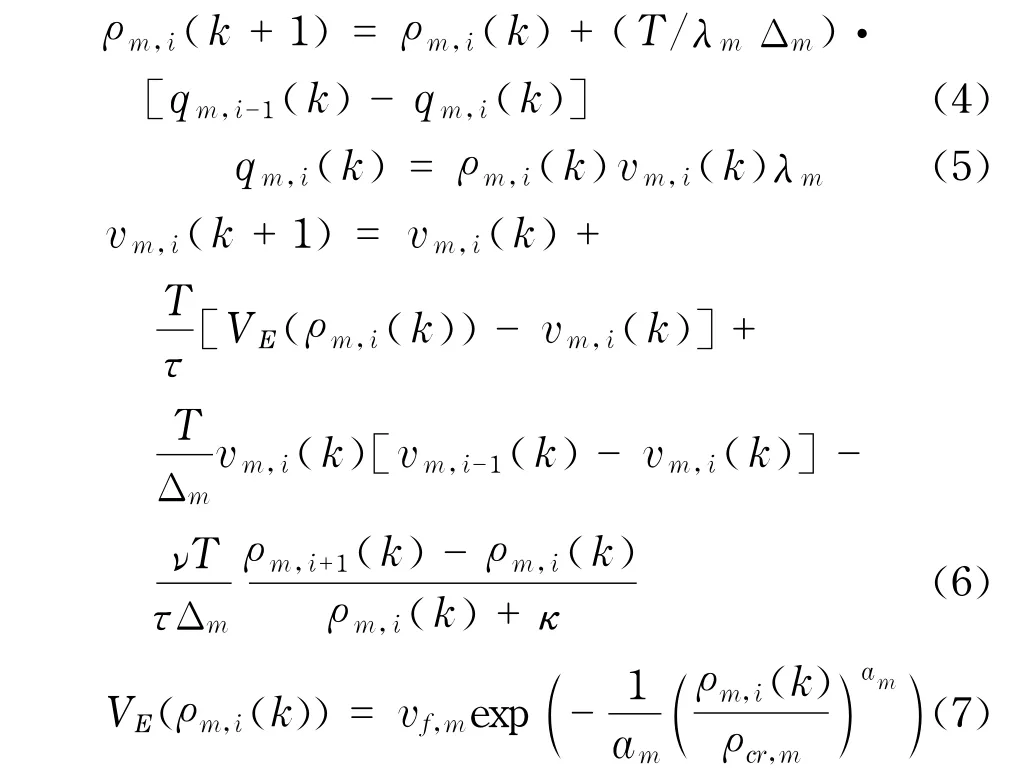
式中,κ、ν、τ为常量参数;VE(·)为稳态速度-密度关系;vf,m、ρcr,m分别为路段m的自由流速度和临界密度;am为与路段m有关的参数.

2.1.2 节点模型

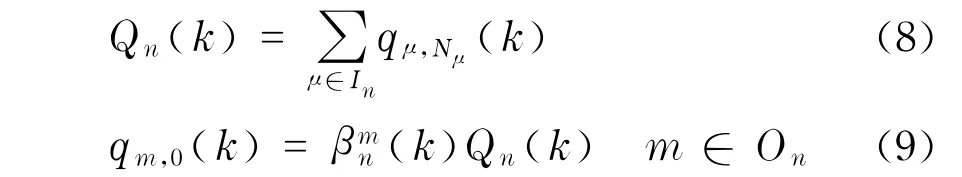
式中,In为流人节点n的路段集合;On为流出节点n的路段集合;Qn为进人节点n的总流量;为转弯比例,即Qn中选择路段m的流量所占比例;qm,0(k)为路段m人口处流量.

2.1.3 起点排队模型

路网起点(包括主线起始点和人口匝道)车辆排队现象可表示为

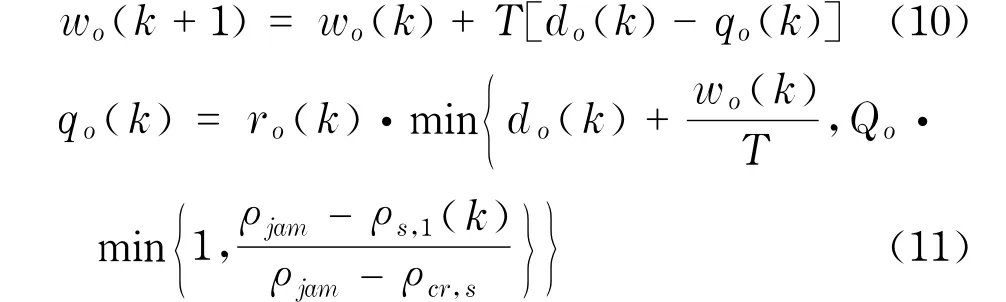
式中,wo为起点o处排队车辆数;do是交通需求;qo是实际流人路网的流量;Qo为最大流人能力; ρjam为阻塞密度;ρs,1为起点下游快速路主线的密度;ro∈[0,1]或{0,1}为匝道调节因子,属于控制输人,由决策变量uo转换而来.

如前所述,决策变量更新周期Ts往往是交通流模型取样周期T的数倍,因此优化得到的决策变量uo(ks)需转化为过程模型中的ro(k).转换方式为：以匝道o为例,根据决策变量uo(ks)取值,得到绿灯时间go(ks)=uo(ks)Ts,并将go(ks)做四舍五人为T的整数倍,假设go(ks)为T的NS倍,NS为正整数,则在时间段[ksz T,ksz T+NS T)内,ro=1;在时间段[ksz T+NS T,(ks+1)z T)内,ro=0.

归纳起来,上述过程模型中,状态向量X包括所有的ρm,i、vm,i和wo,系统外扰D包括所有的do,决策向量包括所有的uo.

2.2 目标函数

采用常用的性能指标“网络总耗时”(total time spent,TTS)作为最优控制问题的目标函数.TTS的表达式为

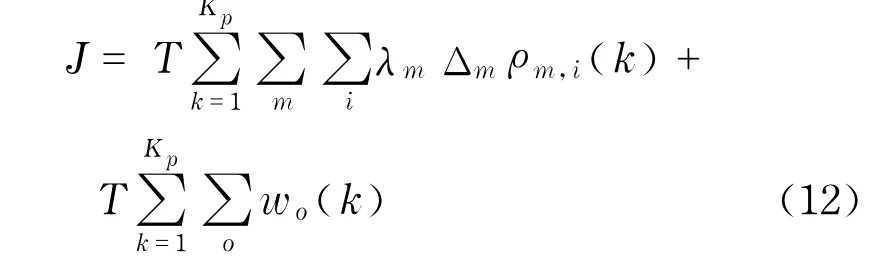
式(12)右侧前一项表示车辆在路网中的总运行时间,后一项则表示路网起点处总排队等候时间.

2.3 优化算法

采用非线性优化中常用的遗传算法求解匝道MPC调节的动态最优控制模型.每一轮滚动优化的算法执行过程如下：

步骤1确定初始条件.设置交通流模型参数、遗传算法的参数(种群规模、等位基因数、交叉概率、变异概率、最大进化代数等)、滚动优化周期Ts和预测时长Kp;

步骤2进化代数为0.随机产生一组初始种群,为二进制编码.种群中每个个体的染色体是潜在解;

步骤3解码.将种群中每个个体的染色体解码为对应的决策变量取值,即所有匝道的调节率ui;

步骤4交通流模型计算.将每个个体解码后获得的匝道调节率ui转换为交通流模型中的匝道调节因子ri,供交通流模型使用.快速路网初始状态根据实测交通数据更新,交通需求为预测时段内的交通需求;

步骤5计算每个个体的适应度.通过上一步骤可获得每个个体在预测时段内的性能指标.个体的适应度函数Fitness取路网总耗时TTS的倒数;

步骤6选择.采用轮盘赌选择方法,选择适应度大的染色体复制,为了加快算法的收敛性,将每代群体中适应度最大的个体直接复制进人下一代;

步骤7交叉.采用单点随机交叉法,将复制得到的种群的染色体随机两两配对交叉两个个体后半部分染色体,得到两个个体;

步骤8变异.以一定的变异概率随机地将子代某些位置的基因实现0-1转换;

步骤9进化代数判别.若达到最大进化代数,转步骤10;否则转步骤3;

步骤10获得匝道调节率.将进化得到的种群中适应度值最大的个体进行解码,转换为匝道调节率,得到匝道信号灯的绿灯时间,作用于交通系统.

3 匝道MPC调节的仿真案例

3.1 路网描述与仿真条件

快速路网拓扑结构如图2(a)所示,路网包含3个起点(O1、O2、O3)和3个终点(J1、J2、J3),节点和路段编号标于图中.路段L1和L8都为4车道,都为2.4 km.路段L3、L5、L7都为2车道和2.1 km,路段L2、L4、L6都为2车道和2.4 km.每一条路段等分为3小段.人口匝道O3处安装有匝道信号灯.从O1到J1一共有两条路径：L1-L3-L5-L7-L8(记为主路径)和L1-L2-L4-L6-L8(记为次路径).交通流模型参数取值参考上海高架快速路实测数据.自由流车速取90 km/h,临界密度取39辆/(km·车道),阻塞密度取160辆/(km·车道),起点O1的单车道通行能力为2 000辆/h,匝道O2和O3的通行能力为1 600辆/h.起点的交通需求见图2(b),模拟需求激增情形,以考察匝道MPC调节对拥挤路网的交通流调控效果.

匝道MPC调节的遗传算法中,种群规模为30,等位基因数目为120,最大进化代数为60,交叉概率为0.7,变异概率为0.01,滚动优化周期为100 s,滚动优化预测时长为20 min.

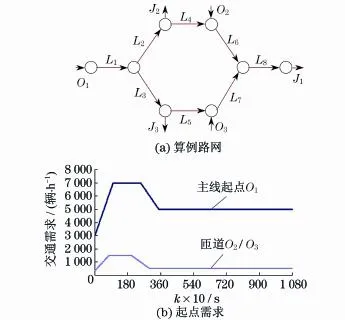
图2 快速路网Fig.2 Freeway network

3.2 匝道MPC调节的基本效果测试

图3为匝道O3的匝道调节率时变轨迹图和排队车辆数.图4(见下页)给出了匝道与主线汇合区域的密度和速度变化轨迹.图5(见下页)给出了主次路径的共用路段的流量.图6(见下页)是k=325时刻路网全局状态截图.

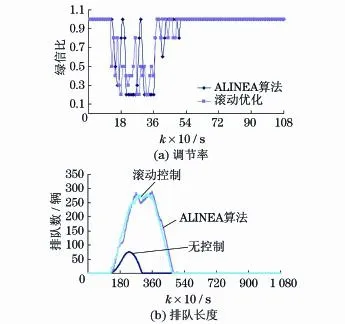
图3 匝道O3的调节率和排队长度时变轨迹Fig.3 On-ramp metering rate and queue trajectories

“不控制”情况下,主路径上,随着主线与匝道需求快速增加,人口匝道与快速路主线汇合区车流密度增大(图4(a)),首先出现拥挤,车速降低(图4 (b)),流量不能维持在较高水平.O3一度出现了排队(图3(b)).汇合区拥挤向主路径上游传播,使得主次路径的共用路段L1也发生阻塞,从而造成L1路段流量有一个急剧跌落又慢慢回升的过程(图5),说明共用路段因出现拥堵而不能发挥应有的通行能力,而随着拥挤消散,通行能力又得以恢复,使得流量上升.相应地,次路径因为共用路段拥堵,也遭受流量先跌落又回升的过程,次路径的通行能力也未充分发挥.TTS是2 789.611辆·h.

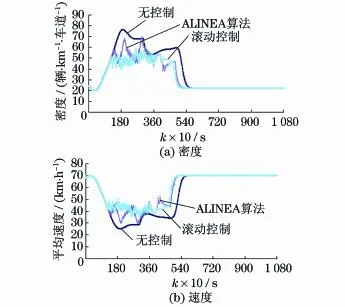
图4 L7第1小段的密度和速度Fig.4 Density and speed of the first segment of link L7

“匝道MPC调节”情况下,匝道O3排队车辆数有所增加(图3(b)),但是显著降低了汇合区瓶颈路段的车流密度(图4(a)),提高了平均车速(图4(b)),缓解了拥堵,需求高峰时段汇合区下游主线始终能维持接近通行能力的高流量水平,更好地发挥了道路通行能力.汇合区拥挤并没有向上游传播至共用路段,共用路段始终处于畅通状态,没有出现因拥挤造成流量先跌落再回升的现象,如图5和图6所示.次路径的流量也不受影响.对比图6(a)和图6(b)可见,不控制时在k=325时刻路段L1最末小段呈红色显示,表明拥挤已经传播至共用路段,造成其阻塞,而匝道MPC调节后在同一时刻路网呈畅通状态.

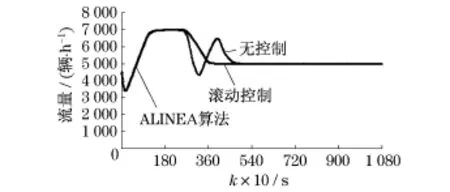
图5 L1第3小段流量时变轨迹Fig.5 Flow of the third segment of link L1

图6 k=325时刻路网全局状态图Fig.6 Snapshot for global network condition at k=325

匝道MPC调节下的TTS是2 653.353辆·h,比不控制减少了4.88%.现实世界中,控制系统每减少1%的TTS,产生的社会经济效益是显著的.对匝道实施MPC调节,虽然增加了匝道排队,但是显著缓解了拥挤,改善了路网整体运营效率.

目前,ALINEA单点匝道控制方法[6]以“简单、实用、能连续平稳地调节交通流”等特点已得到广泛

应用.为更好地理解和评价匝道MPC调节的效果,将ALINEA控制和MPC调节放在同一仿真情境下加以比较.如图3(a)所示,匝道MPC调节下的匝道

调节率变化比ALINEA条件下的更平稳,震荡更小,因而更有利于连续、平稳地调节快速路主线交通流,图4所示匝道与主线汇合区域的密度和速度变化轨迹说明了这一特点.两种控制下的匝道排队情况相似(图3(b)).ALINEA控制下,TTS为2 666.542辆·h,比不控制减少了4.41%,可见ALINEA缓解拥挤的效果低于MPC调节.

3.3 匝道MPC调节的鲁棒性测试

本文还初步探索了MPC调节的鲁棒性,以考察MPC控制器在存在预测误差情形下(模拟真实世界的控制情境)的效果.考察误差的方式为：真实世界的转弯比例在控制器预测的转弯比例的正负百分之五误差范围内随机波动,真实世界的需求在控制器预测的需求的±5%误差范围内随机波动.为降低随机测试的偶然性因素对计算结果的影响,共仿真测试5次,取平均值作为最终测试结果.表1给出了同时存在转弯比例和交通需求预测误差情况下的鲁棒性测试结果.如表1所示,在“真实控制情境”下,MPC控制器仍然具有明显高于ALINEA控制的TTS改善率(5.44%对比4.27%).TTS改善率提高近1.2%,这在现实世界中产生的交通效益和社会经济效益是很大的.这一结果显示,匝道MPC调节具有很好的应用前景,且优于ALINEA.

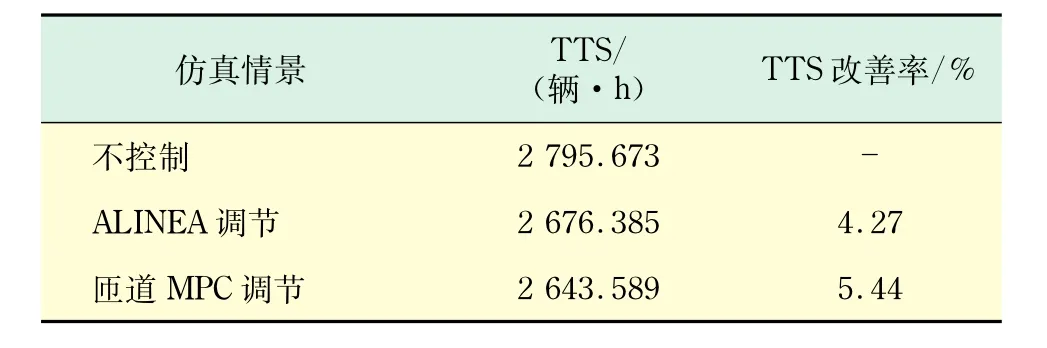
表1 匝道MPC调节的鲁棒性测试结果Tab.1 Robustness test results for MPC ramp metering

4 结束语

瞄准研究前沿,探索了匝道MPC调节这一在线运用非线性优化技术的匝道调节方法,提出了非线性动态时间离散最优控制模型及算法.仿真案例测试结果显示,匝道MPC调节能够显著缓解拥堵,改善路网运行效率,鲁棒性强,控制效果优于ALINEA方法,应用前景良好.下一步将进一步探索匝道MPC调节模型的高效求解算法和控制的鲁棒性.本文成果旨在为我国实施智能化水平更高的匝道调节策略提供理论储备和技术指导.

[1] BELLEMANS T,DE SCHUTTER B,DE MOOR B. Model predictive control for ramp metering of motorway traffic：a case study[J].Control Engineering Practice,2006,14：757-767.

[2] HEGYI A,DE SCHUTTER B,HELLENDOORN H. Model predictive control for optimal coordination of ramp metering and variable speed limits[J].Transportation Research Part C,2005,13(3)：185-209.

[3] KOTSIALOS A,PAPAGEORGIOU M,MANGEAS M,et al.Coordinated and integrated control of motorway networks via non-linear optimal control[J].Transportation Research Part C,2002,10(1)：65-84.

[4] KOTSIALOS A,PAPAGEORGIOU M.Motorway network traffic control systems[J].European Journal of Operational Research,2004,152(2)：321-333.

[5] GAN H C,WEI Y,FAN B,et al.Integrated feedback control of urban freeway networks via nonlinear optimization[C]∥Transportation Research Board.Proceedings of the 86th annual meeting of Transportation Research Board.Washington：2007：0892.

[6] DIAKAKI C,PAPAGEORGIOU M.Simulation studies of integrated corridors control in Glasgow[J].Transportation Research Part C,1997,5(3/4)：211-224.

[7] 丁同强,郑黎黎,常云涛.高速公路人口匝道控制策略研究[J].武汉理工大学学报(交通科学与工程版), 2006,30(2)：755-758.

[8] 郑建湖,董德存,陈洪.城市快速路人口匝道控制策略比较分析[J].计算机测量与控制,2006,14(2)：196-199.

[9] 干宏程,陈建阳,汪晴.高速公路网络路径诱导与匝道控制集成[J].系统工程,2009,27(3)：78-82.

[10] 邹智军.城市快速路人口匝道控制仿真分析[J].同济大学学报(自然科学版),2009,37(2)：631-636.

[11] 柴干,黄琪,方程炜,等.高速公路人口匝道启发式控制的仿真研究[J].系统仿真学报,2009(21)：6829 -6832.

[12] PAPAGEORGIOU M.Dynamic modeling,assignment, and route guidance in traffic networks[J].Transportation Research Part B,1990,24(3)：471-495.

[13] MESSMER M.Papageorgiou,METANET：A macroscopic simulation program for motorway networks[J]. Traffic Engineering and Control,1990,31(8/9)： 466-470,549.

[14] PAPAGEORGIOU M,BLOSSEVILLE J.Modeling and real-time control of traffic flow on the southern part of Boulevard Peripherique in Paris：Part I：Modeling[J]. Transportation Research Part A,1990,24：345-359.

Expressway ramp metering strategy based on model predictive control

GANHong-cheng
(Center for Supernetworks Research,University of Shanghai for Science and Technology,Shanghai 200093,China)

The model predictive control(MPC)based ramp metering strategy was explored,in which online non-linear optimization was applied.The dynamic non-linear time-discrete optimal control model was established and the associated solving algorithm was presented.In the optimal control,a dynamic expressway network traffic flow model was adopted as the process model,and a genetic algorithm was applied to solve the optimization problem.By a simulated case study the efficiency and robustness of the MPCstrategy was tested.The results show that,the MPCstrategy can obviously alleviate congestion and improve the overall network performance.It can control vehicle flow more smoothly comparing to the widely used ALINEA feedback control strategy.The performance criterion of TTS(total time spent)is 1.2%higher,thus it is of good control robustness.

ramp metering;model predictive control;non-linear optimization;dynamic non-linear optimal control model;genetic algorithm;robustness

U 491

A

1007-6735(2011)03-0268-06

2011-05-11

国家自然科学基金资助项目(51008195);上海市教委科研创新资助项目(09YZ205);上海市重点学科建设资助项目(S30504)

干宏程(1978¯),男,副教授.研究方向：交通系统工程、智能交通等.E-mail：hongchenggan@126.com