价值工程在直升机远洋物资保障中的运用

饶 卿 ，谢 骏 ，杨 俊

（1.海军工程大学，湖北 武汉 430033；2.解放军91911部队，海南 三亚 572000）

在远洋条件下，由于受到舰船空间和载重条件的限制，在舰载直升机保障资源的准备中，总会涉及到资源携带量与任务量能否相当的问题。如何在有限的条件下发挥最大的效益，以解决有限的维修资源与可靠性维修之间的矛盾，是远洋条件下舰载机保障必须考虑的问题。

本文运用价值工程的方法，在舰载直升机远洋条件的约束下，对物资准备与预备飞行时间的总体概况进行价值分析，目的在于确保舰载直升机的技术性能，达到预期的任务效果，并最大可能地节省成本，降低费用开支。

1 价值概念

价值工程（VE，Value Engineering）源于二战后的美国。当时通用电气公司工程师麦尔斯发现，人们使用某种材料的目的，在于材料所具有的功能，因此可以考虑用功能相同但价格低廉的替代品，来取代原来昂贵的材料。于是促生了“价值分析”的问世[1]。

尔后，美国防部和政府部门开展价值工程活动，都取得了显著成效。我国在1978年下半年开始推广价值工程活动。价值工程作为一种有效的现代化管理技术，是以提高产品价值为目标的定量分析方法，着重于功能分析，力求用最低的寿命周期费用，可靠地实现必要功能的有组织的创造性活动。其价值的概念不包含政治经济学中社会必要劳动的释义，而是指产品的功能与取得该功能所需成本的比值，是衡量产品经济效益的尺度，是效率公式在价值工程中的具体体现[2-3]，其一般表达式为

价值V=功能F／成本C （1）

维修保障系统的投入，就是维修保障的消耗，包括零部件、器材的消耗，以及人力的消耗等；系统的产出，就是维修保障过程的结果，包括维修后的良好装备或有效的维修服务等。对维修保障系统投入与产出进行分析，就是通过研究维修保障的投入与产出之间稳定的数量依存关系，运用价值工程分析方法，来建立以投入产出为主要目标的评价模型，来合理的分配维修资源[4]，即

维修保障系统的价值V=系统的产出E／系统的投入C （2）

2 远洋物资模型

舰载直升机执行远洋任务时，由于任务飞行时间的不确定性和携带的物资（工具、备件、油料等）有限，所以飞行时间总量受到限制，具体的分析目标就是如何准备与飞行时间相应的物资，以保证飞行任务正常完成的概率最大化。舰载机远洋保障系统中，投入的是保障的资源费用，产出的是舰载机的飞行时间，即

舰载机的价值V=完成任务的时间T／物资费用C（3）

当准备的物资数量大于保障任务飞行的时间，将浪费一定的维修物资费用，比如不易储存的油料和消耗件；当准备的物资数量少于保障任务飞行时间，则不能满足使用的要求，也要造成相应的损失，比如出口运输备件的高费用，任务执行率低等，相较于前者，该损失的后果更为严重。

如何满足一定的使用功能，而所使用的费用又最少，即期望有一个高的价值系数。因此需要选择一个最佳的任务预备飞行时间，来确定物资准备量，使平均损失费用值最小。

根据舰载直升机每50 h定检的特点，以每50 h飞行时间为一单位，设：

C1为每多准备50 h飞行时间的损失费；

C2为每少准备50 h飞行时间的损失费；

P（t）为任务需求飞行时间的概率；

T为预备任务飞行时间。

远洋任务结束时可能出现以下3种情况：

（1）第一种情况，准备时间与实际飞行时间相等。即

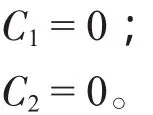
（2）第二种情况，准备时间多于实际飞行时间。则平均损失费为

显然，随着准备时间的增加，该费用逐渐增加。

（3）第三种情况，准备时间少于实际飞行时间。则平均损失费为

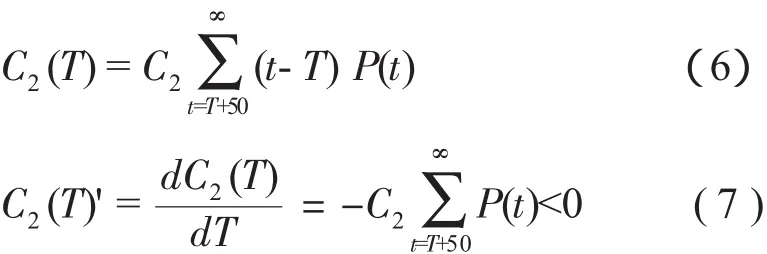
显然，随着准备时间的增加，该费用逐渐减少；

综合这3种情况，平均损失费为

为了确定使平均损失费最小的最佳准备时间T，首先应求出与最佳准备时间对应的临界值，对式（8）求极值，得

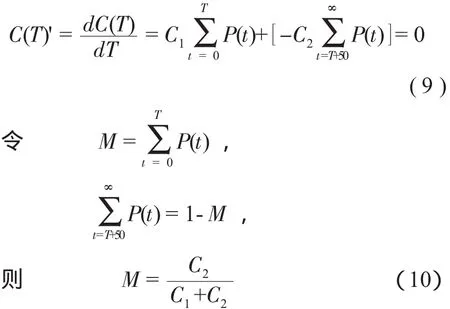
可见，临界值M就是最佳预备飞行时间的累计概率值，是确定最佳准备时间的标准。取累计概率等于或大于临界值M的T值，就是最佳准备时间。

3 实例分析

以某型舰载直升机为例，过去该型机每次执行远洋任务总飞行时间的统计量见表1。

表1 某型机每次远航任务总飞行时间的统计量

以准备时间T=100 h来分析。

第二种情况平均损失费为

C1(100)=P(50)(100-50)C1=5C1

第三种情况平均损失费为

综合来看，当T=100 h，平均损失费为

C(100)=C1(100)+C2(100)=5C1+75C2

利用平均损失费C（T）的一般公式，计算出各种准备时间的平均损失费为

假设C1=0.01，C2=0.02，即损失费用为所需费用的1%和2%，计算各准备时间下的平均损失值，并列入表2中。

表2 各种准备时间的平均损失值

借助MATLAB绘图工具，将时间与费用损失的关系绘制于图1中。

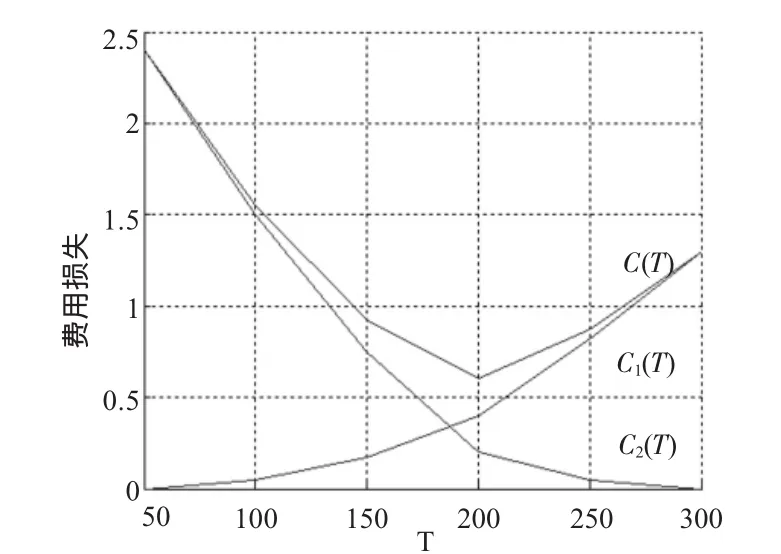
图1 时间与损失费用的关系图

从表2和图1都可以看出，当C1=0.01，C2=0.02时，准备时间T=200 h可使平均损失最小。又因为

从表1可知，累计概率

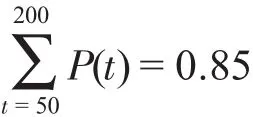
是大于且最接近M=0.67的值，所以，它对应的任务时间，就是最佳准备时间即T=200 h。

这说明最佳准备时间的累计概率值，即临界值M，的确是确定最佳准备时间的标准。其中临界值M由损失费C1、C2决定，它所对应的最佳准备时间随着C1、C2的变化而改变。

4 结束语

本文运用价值工程的理论，简单分析了远洋任务中舰载机保障物资准备的经济性问题。以累积概率值作为临界值，来计算物资准备量的标准，简单可行，为实际工作省去了大量计算。其次，文中所用的是最基本的模型，用于说明思路与方法已经足够，在更复杂的系统性备件工程中，还需要考虑更多的因素影响。

[1]Wilson A R.A study of the best value engineering practice in China[J].The Value Manager，1998，4(2)：3-5

[2]年桂芳.价值工程[M].长春：吉林人民出版社，1986.

[3]杨建昊，金立顺.广义价值工程[M].北京：国防工业出版社，2009.

[4]郑东良.航空维修管理[M].北京：国防工业出版社，2006.